Estados estacionários
Na equação de Schrödinger
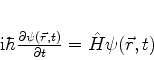 |
(39) |
procuremos soluções da forma
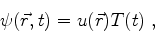 |
(40) |
que são um produto de uma função só de 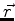 por uma
função só de
por uma
função só de 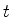 . Explicitando a forma do hamiltoniano,
. Explicitando a forma do hamiltoniano,
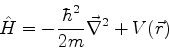 |
(41) |
reescrevemos a Eq.(39) assim:
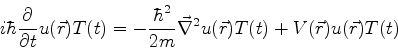 |
(42) |
que pode ser reescrita:
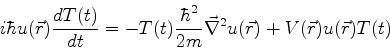 |
(43) |
Dividindo por
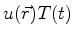 , temos
, temos
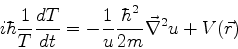 |
(44) |
O primeiro membro não depende de 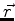 , ou seja, só pode depender de
, ou seja, só pode depender de
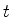 . Ele é igual ao segundo membro, que não pode depender de
. Ele é igual ao segundo membro, que não pode depender de 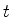 . Logo,
o primeiro membro não depende nem de
. Logo,
o primeiro membro não depende nem de 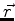 nem de
nem de 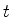 : não dpende
então de nada: é constante. O segundo membro, por força da equação,
é igual ao primeiro, e então também constante. Designemos esta constante
por
: não dpende
então de nada: é constante. O segundo membro, por força da equação,
é igual ao primeiro, e então também constante. Designemos esta constante
por 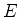 . Teremos então
. Teremos então
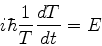 |
(45) |
ou
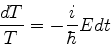 |
(46) |
que é integrada facilmente, dando
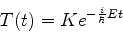 |
(47) |
Logo,
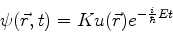 |
(48) |
Note-se que
o que mostra duas coisas importantes:
1. Os
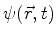 da forma
da forma
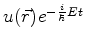 são
autofunções do hamiltoniano.
são
autofunções do hamiltoniano.
2.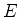 é o autovalor do hamiltoniano, e, portanto, a energia do sistema, quando
neste estado.
é o autovalor do hamiltoniano, e, portanto, a energia do sistema, quando
neste estado.
Estados da forma
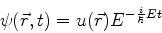 |
(49) |
são chamados estados estacionários. O nome é devido
ao fato de que a densidade de probabilidade de posição,
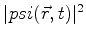 , é independente do tempo, pois
, é independente do tempo, pois
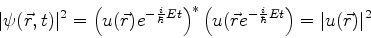 |
(50) |
pois
 .
.
Os estados estacionários são extremamente importantes na
descrição quântica da natureza, não só por representarem
os estados que têm energia definida, mas também porque o
conjnto dos autoestados do hamiltoniano, que são os estados
estacionários, é completo. Isto significa que qualquer estado
pode ser representado como uma combinação linear de estados estacionários.
A determinação dos estados estacionários de um determinado hamiltoniano é
feita normalmente resolvendo-se a equação, dita equação de Schrödinger
independente do tempo,
 |
(51) |
Resolver esta equação significa não só determinar 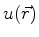 , mas
o par(
, mas
o par(
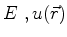 ). O número
). O número 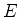 é o autovalor de
é o autovalor de 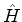 associado
à autofunção
associado
à autofunção 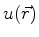 . Problemas desse tipo são chamados, em matemática,
problems de autovalores .
. Problemas desse tipo são chamados, em matemática,
problems de autovalores .
Henrique Fleming 2003
![]() , mas
o par(
, mas
o par(
![]() ). O número
). O número ![]() é o autovalor de
é o autovalor de ![]() associado
à autofunção
associado
à autofunção ![]() . Problemas desse tipo são chamados, em matemática,
problems de autovalores .
. Problemas desse tipo são chamados, em matemática,
problems de autovalores .