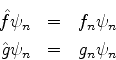Subsections
Operadores
Seja 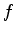 uma quantidade física que caracteriza o estado de um sistema quântico.
Os valores que uma dada quantidade física pode assumir são chamados de
autovalores . O conjunto dos autovalores é o
espectro. Na mecânica
clássica as quantidades físicas são contínuas.7 Na mecânica quântica, não necessariamente. Pode haver espectros discretos
ou espectros contínuos. Vamos supor, para simplificar, que o espectro de
uma quantidade física que caracteriza o estado de um sistema quântico.
Os valores que uma dada quantidade física pode assumir são chamados de
autovalores . O conjunto dos autovalores é o
espectro. Na mecânica
clássica as quantidades físicas são contínuas.7 Na mecânica quântica, não necessariamente. Pode haver espectros discretos
ou espectros contínuos. Vamos supor, para simplificar, que o espectro de 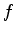 seja discreto.
Os autovalores de
seja discreto.
Os autovalores de 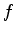 serão denotados por
serão denotados por 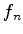 ,
, 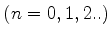 . A função de
onda do sistema,
no estado em que
. A função de
onda do sistema,
no estado em que 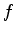 tem o valor
tem o valor 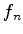 , será denotada por
, será denotada por 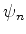 . Essas funções são chamadas
autofunções de
. Essas funções são chamadas
autofunções de 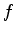 . Para cada uma delas,
. Para cada uma delas,
Um dos princípios básicos da mecânica quântica é este:
(I) O conjunto das autofunções de uma quantidade física 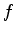 é completo. Isto é, dada uma função de onda
qualquer
é completo. Isto é, dada uma função de onda
qualquer 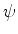 do sistema, podemos expandí-la em autofunções de
do sistema, podemos expandí-la em autofunções de 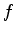 assim:
assim:
onde os 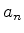 são números complexos.
são números complexos.
(II)Fazendo-se uma medida de 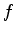 em
em 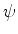 , a probabilidade de se obter o valor
, a probabilidade de se obter o valor 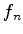 é dada
por
é dada
por 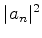 .
.
Em conseqüência, devemos ter
pois
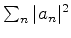 é a probabilidade de, medindo-se
é a probabilidade de, medindo-se 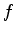 , obter-se qualquer um dos valores
possíveis.
, obter-se qualquer um dos valores
possíveis.
Temos, então, o resultado
Por outro lado, temos
logo,
de onde se conclui que
Finalmente, usando
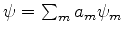 , temos
, temos
de onde se conclui que
Diz-se então que as autofunções são ortogonais.
Valor médio
Vamos introduzir agora o conceito de valor médio 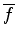 da quantidade
física
da quantidade
física  em um dado estado. Sejam
em um dado estado. Sejam  os valores possíveis de
os valores possíveis de 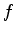 , ou seja, seus
autovalores . Sejam
, ou seja, seus
autovalores . Sejam 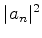 as probabilidades de cada um dos autovalores , no estado em
questão. Define-se então o valor médio como
as probabilidades de cada um dos autovalores , no estado em
questão. Define-se então o valor médio como
Usa-se também a notação
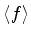 , para a mesma quantidade.
Queremos encontrar uma expressão para
, para a mesma quantidade.
Queremos encontrar uma expressão para 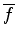 em termos da função de onda do
estado considerado. Seja
em termos da função de onda do
estado considerado. Seja 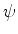 esta função. Para fazer isso vamos associar à quantidade
física
esta função. Para fazer isso vamos associar à quantidade
física 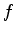 um operador linear
um operador linear 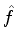 que atua sobre as funções de onda. Seja
que atua sobre as funções de onda. Seja 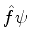 a função obtida quando
a função obtida quando 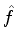 atua sobre
atua sobre 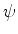 . Queremos, de
. Queremos, de 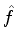 , que
, que
para qualquer estado 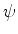 (lembre-se que estipulamos que as quantidades físicas deveriam
ser expressões bilineares na função de onda). Então,
(lembre-se que estipulamos que as quantidades físicas deveriam
ser expressões bilineares na função de onda). Então,
onde usamos
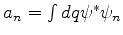 , obtido anteriormente. Vemos, primeiramente, que
, obtido anteriormente. Vemos, primeiramente, que
Ora,
de maneira que 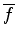 é linear, e que
é linear, e que
Sumarizando:
Os valores assumidos por uma quantidade física são reais. Portanto, os valores médios
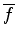 de uma quantidade física são também reais, como se vê de
de uma quantidade física são também reais, como se vê de
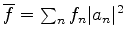 . Note-se (exercício fácil), que, se o estado
for uma autofunção de
. Note-se (exercício fácil), que, se o estado
for uma autofunção de 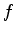 , o valor médio
, o valor médio 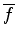 coincide com o autovalor de
coincide com o autovalor de 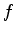 nesse estado.
nesse estado.
Do fato de 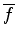 ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
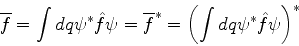 |
(5) |
Ora,
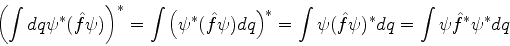 |
(6) |
onde 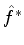 é definido assim: se
é definido assim: se
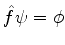 , então
, então 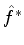 é o operador
tal que
é o operador
tal que
 .8
Então,
.8
Então,
Vamos definir o operador transposto 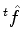 do operador
do operador 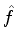 . Sejam
. Sejam 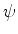 e
e 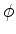 funções arbitárias. Então
funções arbitárias. Então 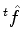 é tal que
é tal que
Por exemplo, para 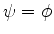 i,
i,
Da condição de realidade de 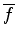 , Eq.(6), temos
, Eq.(6), temos
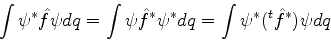 |
(7) |
Comparando os dois extremos vemos que
Operadores com esta propriedade são ditos
hermiteanos. Logo, os operadores associados a
quantidades físicas são operadores lineares hermiteanos.
Podemos, formalmente, considerar quantidades físicas complexas, isto é, cujos autovalores são
complexos. Por exemplo, dadas as coordenadas 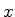 e
e 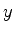 ,podemos considerar a quantidade
,podemos considerar a quantidade 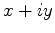 . Seja
. Seja
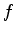 uma quantidade desse tipo, e seja
uma quantidade desse tipo, e seja 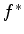 a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de
a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de 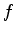 . À quantidade
. À quantidade 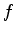 corresponde o operador
corresponde o operador 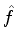 . Denotemos por
. Denotemos por 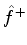 o operador correspondente à quantidade
o operador correspondente à quantidade 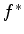 . Este operador é
denominado o adjunto
de
. Este operador é
denominado o adjunto
de 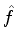 .
.
O valor médio da quantidade 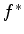 é dado por
é dado por
onde apenas adaptamos a definição de média de um operador.
Ora,
logo,
Mas
Ou seja,
Comparando, temos
Em palavras, o adjunto é o transposto do conjugado.
A condição de hermiticidade de um operador, escrita anteriormente como
pode agora ser escrita:
e os operadores hermiteanos são aqueles que coincidem com os adjuntos. Daí serem
chamados também de auto-adjuntos.
Vamos agora mostrar que a ortogonalidade das autofunções de um operador hermiteano
pode ser demonstrada diretamente.
Sejam 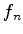 e
e 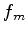 dois autovalores diferentes do operador hermiteano
dois autovalores diferentes do operador hermiteano 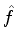 .
Sejam
.
Sejam 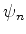 e
e 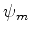 as autofunções correspondentes. Então,
as autofunções correspondentes. Então,
Multiplicando a primeira por 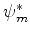 , temos
, temos
e
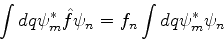 |
(10) |
Tomando o complexo conjugado de (9) e multiplicando por 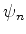 ,
temos
,
temos
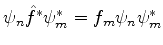 . Integrando,
. Integrando,
 |
(11) |
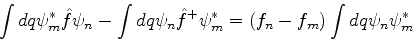 |
(12) |
Mas
pois 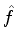 é hermiteano. Logo, o primeiro termo de (12) é zero.
Conseqüentemente,
é hermiteano. Logo, o primeiro termo de (12) é zero.
Conseqüentemente,
e, como 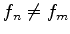 , segue que
, segue que
Sejam 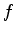 e
e 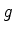 duas quantidades físicas que podem ter valores definidos simultaneamente.
Sejam
duas quantidades físicas que podem ter valores definidos simultaneamente.
Sejam 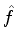 e
e 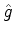 seus operadores. Os autovalores da soma
seus operadores. Os autovalores da soma 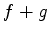 são a soma dos
autovalores de
são a soma dos
autovalores de 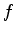 e de
e de 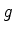 . Considere o operador
. Considere o operador
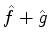 , e sejam
, e sejam 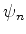 as
autofunções comuns a
as
autofunções comuns a 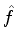 e
e 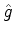 . Então,
. Então,
e, portanto,
Este resultado pode ser generalizado para funções de onda quaisquer, assim:
Neste caso, tem-se
A multiplicação de operadores é definida assim:
Suponhamos que 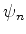 seja autofunção comum a
seja autofunção comum a 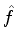 e
e 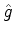 . Então,
. Então,
e
Logo, para as autofunções simultaneas, temos
Isto não é suficiente para se concluir que o operador
Contudo, como o conjunto das autofunções 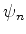 é completo, temos, dada uma função de onda
arbitrária, que
é completo, temos, dada uma função de onda
arbitrária, que
e
Logo, o operador
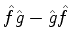 é zero como operador, pois leva qualquer
função ao valor zero. Note-se que isto foi demonstrado para dois operadores que possuem um
conjunto completo de autofunções comuns. No caso geral, esse comutador,
é zero como operador, pois leva qualquer
função ao valor zero. Note-se que isto foi demonstrado para dois operadores que possuem um
conjunto completo de autofunções comuns. No caso geral, esse comutador,
é diferente de zero.
Henrique Fleming 2003
![]() é completo. Isto é, dada uma função de onda
qualquer
é completo. Isto é, dada uma função de onda
qualquer ![]() do sistema, podemos expandí-la em autofunções de
do sistema, podemos expandí-la em autofunções de ![]() assim:
assim:
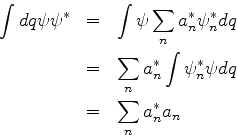
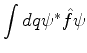
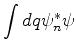
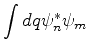
![]() ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
![]() e
e ![]() ,podemos considerar a quantidade
,podemos considerar a quantidade ![]() . Seja
. Seja
![]() uma quantidade desse tipo, e seja
uma quantidade desse tipo, e seja ![]() a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de
a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de ![]() . À quantidade
. À quantidade ![]() corresponde o operador
corresponde o operador ![]() . Denotemos por
. Denotemos por ![]() o operador correspondente à quantidade
o operador correspondente à quantidade ![]() . Este operador é
denominado o adjunto
de
. Este operador é
denominado o adjunto
de ![]() .
.
![]() é dado por
é dado por
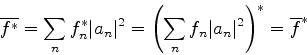
![]() e
e ![]() dois autovalores diferentes do operador hermiteano
dois autovalores diferentes do operador hermiteano ![]() .
Sejam
.
Sejam ![]() e
e ![]() as autofunções correspondentes. Então,
as autofunções correspondentes. Então,