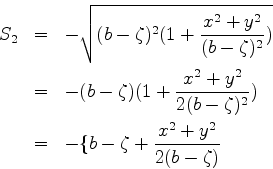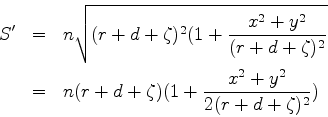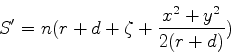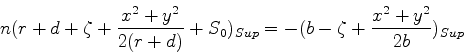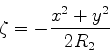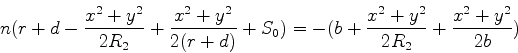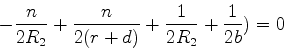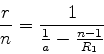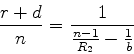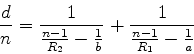Subsections
A ótica geométrica é o limite da ótica ondulatória
para  . Na realidade, a ótica geométrica é uma
aproximação que vale quando a difração é
desprezível. Isto ocorre quando os obstáculos que as
ondas de luz encontram têm dimensões grandes em relação
ao comprimento de onda delas. Uma maneira de garantir que isto sempre
se verifique é tomar ondas de comprimento bem pequeno. Por isso
se diz ``no limite
. Na realidade, a ótica geométrica é uma
aproximação que vale quando a difração é
desprezível. Isto ocorre quando os obstáculos que as
ondas de luz encontram têm dimensões grandes em relação
ao comprimento de onda delas. Uma maneira de garantir que isto sempre
se verifique é tomar ondas de comprimento bem pequeno. Por isso
se diz ``no limite  ''.
Suponhamos que a propagação da luz se dê em um meio material
simples, descrito por uma constante dielétrica
''.
Suponhamos que a propagação da luz se dê em um meio material
simples, descrito por uma constante dielétrica  e uma
permeabilidade magnética
e uma
permeabilidade magnética  . Se o meio for homogêneo e se
. Se o meio for homogêneo e se
 e
e  , teremos as equações de onda
, teremos as equações de onda
 |
(1018) |
para o campo elétrico, e
 |
(1019) |
com
Estas equações seguem diretamente das equações de Maxwell, como
vimos anteriormente. Se a onda for monocromática, a dependência temporal
será
e a equação 1020 fica
 |
(1020) |
e, pondo
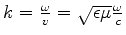 ,
temos
,
temos
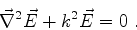 |
(1021) |
Vamos nos restringir a ondas escalares, ou seja, vamos ignorar que os campos
são vetores. Perderemos com isso toda a variedade de fenômenos associados
à polarização. No entanto, muitos fenômenos, aqueles que são
diretamente associados ao caráter ondulatório, ao fenômeno da
interferência, serão ainda razoavelmente descritos. Seja 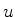 o campo
escalar (por exemplo, uma das componentes de
o campo
escalar (por exemplo, uma das componentes de 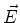 ). A equação
é
). A equação
é
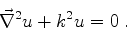 |
(1022) |
Vamos procurar soluções da forma
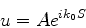 |
(1023) |
com
 , onde
, onde  e
e 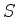 são funções de
são funções de  que
variam lentamente e que não tendem a
que
variam lentamente e que não tendem a  quando
quando  cresce.
cresce.
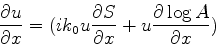 |
(1024) |
com termos análogos para as derivadas em 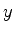 e
e 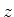 . Assim, temos
. Assim, temos
Isto pode ser abreviado assim:
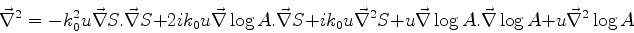 |
(1027) |
Logo, a equação fica:
 |
(1028) |
ou ainda,
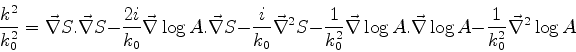 |
(1029) |
No limite
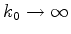 , temos
, temos
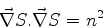 |
(1030) |
e
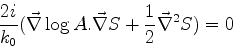 |
(1031) |
de maneira que as equações são:
que são as equações básicas da ótica geométrica.41
de onde segue que
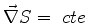 , ou seja,
, ou seja,
Neste caso
e
 |
(1034) |
Logo,
 |
(1035) |
e as superfícies
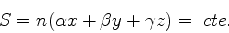 |
(1036) |
são planos. Ora, as superfícies  são as frentes de onda, logo
a propagação aqui descrita é a de ondas planas. Note-se que, se
são as frentes de onda, logo
a propagação aqui descrita é a de ondas planas. Note-se que, se 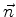 é um vetor unitário, isto é, se
é um vetor unitário, isto é, se
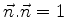 , temos, com
, temos, com
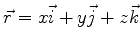 ,
,
e
Comparando com a Eq.(1037) vemos que  ,
, 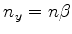 e
e
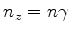 , razão pela qual
, razão pela qual 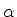 ,
, 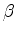 e
e 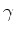 são os `` cosenos
diretores'' da direção
são os `` cosenos
diretores'' da direção 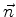 .
Vamos ver agora o casode dois meios homogêneos separados por um plano
em
.
Vamos ver agora o casode dois meios homogêneos separados por um plano
em 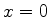 Temos
Temos
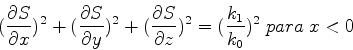 |
(1037) |
e
 |
(1038) |
Seja 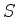 um plano cuja normal não tem componente ao longo de
um plano cuja normal não tem componente ao longo de 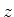 .
Então
.
Então
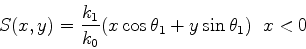 |
(1039) |
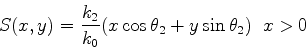 |
(1040) |
Para 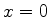 ,
,
 |
(1041) |
ou
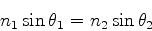 |
(1042) |
que é a lei de Snell-Descartes.
Considere a seguinte solução da equação do eikonal, dotada
de simetria esférica:
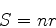 |
(1043) |
onde 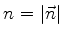 e
e  . Temos
. Temos
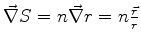 e, portanto,
e, portanto,
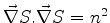 . As
superfícies
. As
superfícies  são, neste caso, as superfícies
são, neste caso, as superfícies 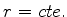 ,
ou seja, as frentes de onda são superfícies esféricas com centro
na origem. Para que se trate verdadeiramente de uma solução da equação
do eikonal, é preciso ainda que a Eq.(1035) seja satisfeita:
,
ou seja, as frentes de onda são superfícies esféricas com centro
na origem. Para que se trate verdadeiramente de uma solução da equação
do eikonal, é preciso ainda que a Eq.(1035) seja satisfeita:
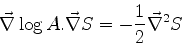 |
(1044) |
Ora,
ou
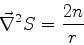 |
(1045) |
É necessário então que
ou, que
Segue então que
Portanto,
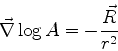 |
(1046) |
Mas
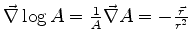 e,
conseqüentemente,
e,
conseqüentemente,
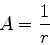 |
(1047) |
Podemos então contruir a onda 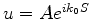 (ver Eq.(1025)).
(ver Eq.(1025)).
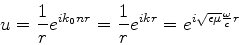 |
(1048) |
que é a parte espacial de uma onda esférica.
Considere a curva descrita pela extremidade do vetor 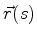 , onde
, onde
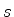 é o comprimento da curva. Seja
é o comprimento da curva. Seja 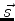 o vetor tangente à curva em
cada ponto. Se a curva for uma reta, a tangente em todos os pontos tem a
mesma direção. Em curvas que não são retas, a tangente ``gira''
quando se percorre a curva. Este movimento da tangente é usado para
definir a curvatura de uma curva como o vetor
o vetor tangente à curva em
cada ponto. Se a curva for uma reta, a tangente em todos os pontos tem a
mesma direção. Em curvas que não são retas, a tangente ``gira''
quando se percorre a curva. Este movimento da tangente é usado para
definir a curvatura de uma curva como o vetor
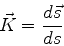 |
(1049) |
Como o vetor tangente é
 , vemos que a
curvatura é
, vemos que a
curvatura é
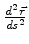 , ou seja é a ``aceleração'',
se
, ou seja é a ``aceleração'',
se 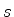 for tomado como o tempo.
for tomado como o tempo.
Considere, por exemplo, um círculo, de equação 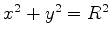 .
Temos
.
Temos
e segue facilmente que
ou,
Como
 , temos
, temos
que dá
Para a curvatura então temos:
ou
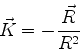 |
(1050) |
A curvatura é, então, um vetor, cujo módulo é
A curvatura do círculo é tanto maior quanto menor o raio, o que
mostra que a definição acompanha a idéia intuitiva.
Voltemos ao caso geral. Como o vetor tangente 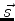 tem módulo
tem módulo  42, de
42, de
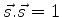 segue que
segue que
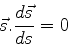 |
(1051) |
ou seja,
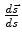 é perpendicular a
é perpendicular a 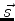 . Logo,
. Logo,
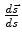 pode ser escrito na forma
pode ser escrito na forma
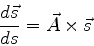 |
(1052) |
onde 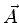 é um vetor a determinar43De fato, considere
o vetor
é um vetor a determinar43De fato, considere
o vetor
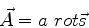 |
(1053) |
onde 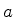 é uma constante. Temos
é uma constante. Temos
 e
e
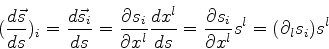 |
(1054) |
enquanto
e o último termo é nulo, pois
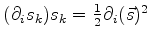 ,
e
,
e
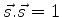 .
Conseqüentemente,
.
Conseqüentemente,
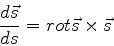 |
(1055) |
Até agora falamos genericamente de curvas. Consideremos agora curvas que sejam raios
de luz. Como vimos anteriormente, os raios de luz são ortogonais às superfícies
 , ou seja, têm, em cada ponto dessas superfícies, a direção de
, ou seja, têm, em cada ponto dessas superfícies, a direção de
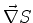 . Em símbolos,
. Em símbolos,
 |
(1056) |
Daí decorre que
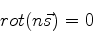 |
(1057) |
onde usamos o fato conhecido 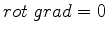 . Da Eq.(1059)
segue que
. Da Eq.(1059)
segue que
e, portanto, que
e, finalmente,
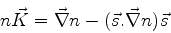 |
(1058) |
onde 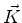 é o vetor curvatura do raio. Uma conseqüência
imediata da Eq.(1060) é que em meios homogêneos
(
é o vetor curvatura do raio. Uma conseqüência
imediata da Eq.(1060) é que em meios homogêneos
( constante) a curvatura é nula, e os raios são retas. Uma
outra aplicação é a seguinte: quando o Sol está muito
baixo, no nascente ou no poente, os raios que atingem um
observador são aproximadamente horizontais. O índice de
refração da atmosfera diminui com a altitude, logo
constante) a curvatura é nula, e os raios são retas. Uma
outra aplicação é a seguinte: quando o Sol está muito
baixo, no nascente ou no poente, os raios que atingem um
observador são aproximadamente horizontais. O índice de
refração da atmosfera diminui com a altitude, logo
 aponta para o centro da Terra, ou seja, é
vertical. Então, na Eq.(1060), o segundo termo do
segundo membro é muito pequeno.
Conclui-se que a curvatura
desses raios é paralela a
aponta para o centro da Terra, ou seja, é
vertical. Então, na Eq.(1060), o segundo termo do
segundo membro é muito pequeno.
Conclui-se que a curvatura
desses raios é paralela a
 , apontando para o
centro da Terra. Os raios, isto é, se curvam para baixo. Em
conseqüência, o observador, que interpreta sempre o raio como
uma reta, ``vê'' o Sol mais alto do que está na realidade. De
fato, isto explica por que se vê o Sol ainda um pouco depois de
ele ter se posto.
, apontando para o
centro da Terra. Os raios, isto é, se curvam para baixo. Em
conseqüência, o observador, que interpreta sempre o raio como
uma reta, ``vê'' o Sol mais alto do que está na realidade. De
fato, isto explica por que se vê o Sol ainda um pouco depois de
ele ter se posto.
No tratamento elementar da ótica geométrica obtém-se, por
constrções geométricas utilizando a lei de Snell-Descartes, a
equação
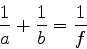 |
(1059) |
sendo 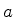 a distância do objeto à lente (supostamente de espessura
desprezíivel),
a distância do objeto à lente (supostamente de espessura
desprezíivel), 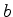 a distância da imagem à lente, e
a distância da imagem à lente, e 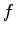 a distância
focal da lente, que é dada por
a distância
focal da lente, que é dada por
sendo  o íindice de refração do vidro,
o íindice de refração do vidro, 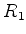 e
e 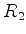 os raios das
superfíicies esféricas da lente. O significado de
os raios das
superfíicies esféricas da lente. O significado de 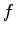 pode ser obtido
facilmente da Eq.(1061): tomando-se
pode ser obtido
facilmente da Eq.(1061): tomando-se 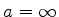 , tem-se
, tem-se
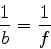 |
(1060) |
que mostra ser 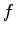 a distância a que se forma a imagem quando o objeto
está no infinito. Na Eq.(1061) a lente é suposta de
espessura zero, e a distância à lente é confundida com a distância
ao centro da lente.
a distância a que se forma a imagem quando o objeto
está no infinito. Na Eq.(1061) a lente é suposta de
espessura zero, e a distância à lente é confundida com a distância
ao centro da lente.
Vamos tratar esse problema com o uso da equação do eikonal.
Não haverá qualquer dificuldade em tratar o caso de lentes
espessas, e o caminho estará aberto também para o tratamento
de lentes cujas faces não sejam superfícies esféricas.
O ponto  da figura designa a posição do objeto, de
coordenadas
da figura designa a posição do objeto, de
coordenadas 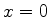 ,
, 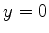 e
e  . O eixo
. O eixo 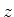 é a direção
de incidência: é a reta que une
é a direção
de incidência: é a reta que une  ao centro da lente,
ao centro da lente, 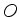 .
.
Um raio partido de  e incidente sobre a lente, encontra-a no
ponto
e incidente sobre a lente, encontra-a no
ponto 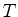 , pertencente a uma superfície esférica de raio
, pertencente a uma superfície esférica de raio
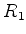 (a primeira face da lente). O centro dessa superfície
esférica está no ponto de coordenadas
(a primeira face da lente). O centro dessa superfície
esférica está no ponto de coordenadas 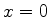 ,
, 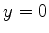 ,
, 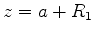 .
As coordenadas de
.
As coordenadas de 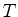 são
são 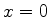 ,
, 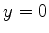 ,
, 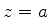 . Um ponto vizinho
à lente tem coordenada
. Um ponto vizinho
à lente tem coordenada  , com
, com 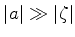
As ondas esféricas emitidas de  têm o eikonal
têm o eikonal
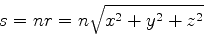 |
(1061) |
com 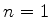 (região externa à lente), ou seja, mais
explicitamente,
(região externa à lente), ou seja, mais
explicitamente,
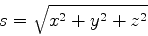 |
(1062) |
Perto da primeira face da lente o eikonal é
Restringindo-nos a pequenas aberturas, basta considerar valores
pequenos de 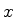 e
e 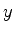 . Então,
. Então,
ou seja,
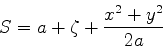 |
(1064) |
A equação da superfície da primeira face da lente é
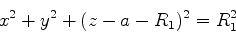 |
(1065) |
Podemos agora resolver o problema da primeira refração na
lente.
A figura mostra um raio saindo de  e incidindo sobre a lente, e
o raio refratado (que existe só dentro da lente). Prolongando-se
o raio refratado até que atinja o eixo da lente, determina-se o
ponto
e incidindo sobre a lente, e
o raio refratado (que existe só dentro da lente). Prolongando-se
o raio refratado até que atinja o eixo da lente, determina-se o
ponto 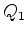 . Esse raio,
. Esse raio, 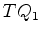 , existiria se a propagação se
desse num meio homogêneo de índice de refração igual
ao da lente,
, existiria se a propagação se
desse num meio homogêneo de índice de refração igual
ao da lente,  . O eikonal do raio refratado é, então,
. O eikonal do raio refratado é, então,
 |
(1066) |
pois as coordenadas de 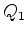 são
são 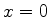 ,
, 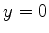 ,
, 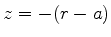 . Para
pontos próximos à primeira face da lente temos
. Para
pontos próximos à primeira face da lente temos  ,
com
,
com 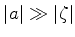 . Então,
. Então,
 |
(1067) |
ou, aproximadamente,
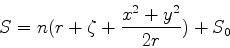 |
(1068) |
onde  é uma constante. Em geral essa constante aditiva é
desnecessária, embora esteja sempre presente, já que, sendo a
equação do eikonal uma equação para
é uma constante. Em geral essa constante aditiva é
desnecessária, embora esteja sempre presente, já que, sendo a
equação do eikonal uma equação para 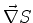 ,
se um
,
se um 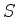 é solução,
é solução, 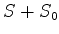 também o será,
também o será,  sendo uma constante arbitrária. Neste problema que estamos
estudando, imporemos a continuidade do eikonal numa determinada
superfície, e, para isso ser possível, é necessário
incluir o
sendo uma constante arbitrária. Neste problema que estamos
estudando, imporemos a continuidade do eikonal numa determinada
superfície, e, para isso ser possível, é necessário
incluir o  .
.
A condição de contorno é que o eikonal (a fase!) varie
continuamente ao atravessar a face da lente. Se isto não lhe
parece intuitivo, note que é sob essa condição que se obtém a
lei de Snell-Descartes para a refração numa superfície plana, o
que pode ser considerado uma ``verificação experimental'' do fato.
Para pequenas aberturas os pontos que satisfazem a
Eq.(1067) da superfície são tais que
 |
(1069) |
ou, como 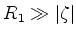 ,
,
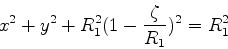 |
(1070) |
ou ainda,
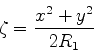 |
(1071) |
Devemos ter a coincidência dos dois eikonais sobre a
superfície da lente. Então,
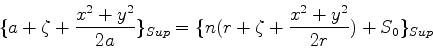 |
(1072) |
que leva a
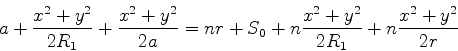 |
(1073) |
ou seja,
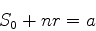 |
(1074) |
e
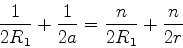 |
(1075) |
ou ainda
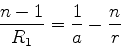 |
(1076) |
Esta equção resolve o problema da refração por um dioptro esférico.
A equação da segunda face, se 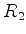 é o seu raio e
é o seu raio e 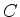 o
seu centro, é
o
seu centro, é
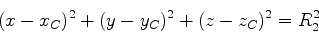 |
(1077) |
ou
 |
(1078) |
Para pontos próximos à segunda face, temos
com
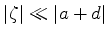 . Então,
. Então,
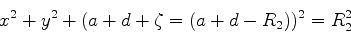 |
(1079) |
ou
 |
(1080) |
e, usando o fato de que 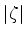 é pequeno,
é pequeno,
 |
(1081) |
e, finalmente,
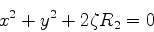 |
(1082) |
que podemos por na forma
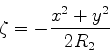 |
(1083) |
O eikonal do segundo raio refratado é
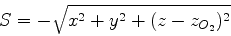 |
(1084) |
onde 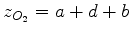 , o que dá
, o que dá
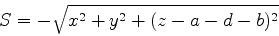 |
(1085) |
Perto da segunda face da lente, temos
 |
(1086) |
ou
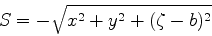 |
(1087) |
Para pequenas aberturas,
ou
 |
(1088) |
O eikonal do primeiro raio refratado, quando ele atinge as proximidades
da segunda face da lente, é
 |
(1089) |
onde resolvemos denotá-lo por 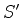 para distinguí-lo do eikonal
do segundo raio refratado. Temos, após uma simplificação,
para distinguí-lo do eikonal
do segundo raio refratado. Temos, após uma simplificação,
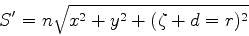 |
(1090) |
Para pequenas aberturas,
ou, finalmente,
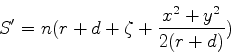 |
(1091) |
Devemos então ter, na segunda face,
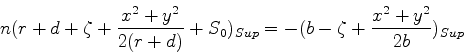 |
(1092) |
onde o cálculo deve ser feito para os pontos da segunda superfície da
lente, ou seja, para
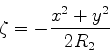 |
(1093) |
Temos então
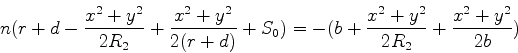 |
(1094) |
que dá as equações
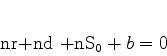 |
(1095) |
e
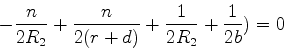 |
(1096) |
ou
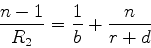 |
(1097) |
A solução do problema consiste em combinar as
Eqs.(1097) e (1099) para eliminar 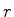 . Da
Eq.(1097) temos
. Da
Eq.(1097) temos
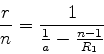 |
(1098) |
e, da Eq.(1099),
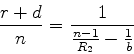 |
(1099) |
Subtraindo a primeira da segunda, temos
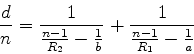 |
(1100) |
que é a equação dos focos conjugados para uma lente de espessura  e para pequenas aberturas. Se
e para pequenas aberturas. Se  , obtém-se
, obtém-se
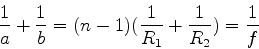 |
(1101) |
que é a equação usual, para lentes delgadas.
Henrique Fleming 2003
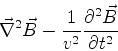
![]() o campo
escalar (por exemplo, uma das componentes de
o campo
escalar (por exemplo, uma das componentes de ![]() ). A equação
é
). A equação
é
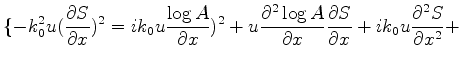
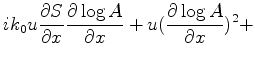
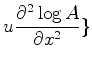
![$\displaystyle \{-k_0^2u[(\frac{ \partial S}{\partial x})^2
+ (\frac{ \partial S}{\partial y})^2 +(\frac{ \partial S}{\partial z})^2
] +$](img2859.png)
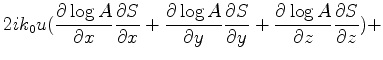
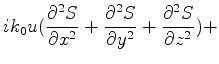
![$\displaystyle u[(\frac{ \partial\log{A}}{\partial x})^2 +
(\frac{ \partial\log{A}}{\partial y})^2+
(\frac{ \partial\log{A}}{\partial z})^2] +$](img2862.png)
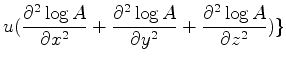
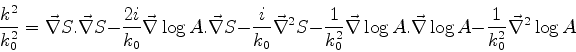
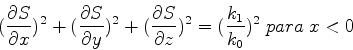

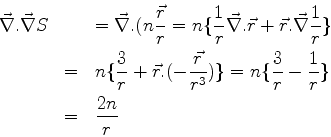
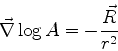
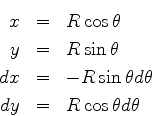
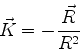
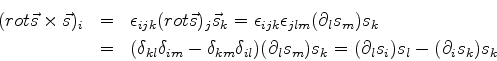
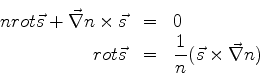

![]() têm o eikonal
têm o eikonal
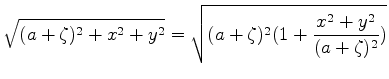
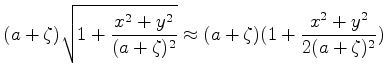
![]() e incidindo sobre a lente, e
o raio refratado (que existe só dentro da lente). Prolongando-se
o raio refratado até que atinja o eixo da lente, determina-se o
ponto
e incidindo sobre a lente, e
o raio refratado (que existe só dentro da lente). Prolongando-se
o raio refratado até que atinja o eixo da lente, determina-se o
ponto ![]() . Esse raio,
. Esse raio, ![]() , existiria se a propagação se
desse num meio homogêneo de índice de refração igual
ao da lente,
, existiria se a propagação se
desse num meio homogêneo de índice de refração igual
ao da lente, ![]() . O eikonal do raio refratado é, então,
. O eikonal do raio refratado é, então,
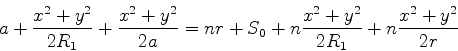
![]() é o seu raio e
é o seu raio e ![]() o
seu centro, é
o
seu centro, é
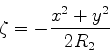
![]() . De fato,
uma onda esférica que sai da origem é
. De fato,
uma onda esférica que sai da origem é