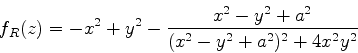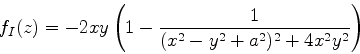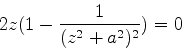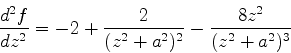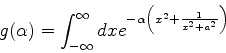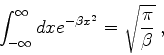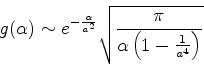Subsections
Entre as muitas excelências do grande livro Quantum
Mechanics, de L. D. Landau e E. M. Lifshitz[3],
está o apêndice
denominado Mathematical Appendices, onde, de uma forma
unificada, são tratadas várias das funções especiais necessárias
ao longo do texto. Essa unificação é tornada possível pelo uso
do método de Laplace, uma genial técnica de resolução de
certas equações diferenciais ordinárias inventada pelo grande
matemático francês enquanto redigia seu Théorie analytique
des probabilités.
O método faz uso intenso da integração no plano complexo, o que
abre caminho para a utilização do método do ponto sela, para
o estudo do comportamento assintótico das soluções. É esta
combinação de técnicas que faz com que os métodos apresentados
no apêndice citado se destaquem pela elegância e concisão,
para não mencionar a potência.
O tratamento dado por Landau é talvez excessivamente breve, o que
torna o material do apêndice acessível para poucos. Este artigo
pretende, estendendo-se mais longamente sobre o tema, torná-lo
acessível a um número maior de estudantes.
Minha principal fonte foi o grande tratado de Edouard
Goursat[4], Cours d'Analyse Mathématique. Uma
exposição mais detalhada e ambiciosa, escrita com a graça de sempre,
encontra-se em Hille[5], abundante em notas históricas
e aplicações elegantes. Para o método do ponto sela minha
referência preferida é Courant, Hilbert[6]. Para saber
mais sobre Laplace e seu tratado de probabilidades veja o notável
Dictionary of Scientific Biography[7] ou, mais especificamente,
a biografia de Laplace por Gillispie[8], um dos editores
do dicionário citado.
Laplace, após ter inventado a transformação que leva o seu
nome38, generalizou-a de
várias formas. A que
nos interessa aqui, uma generalização para o plano complexo, serve para
resolver certas equações diferenciais ordinárias
muito comuns nas aplicações. São equações da forma
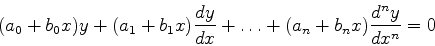 |
(933) |
que vamos também, de forma abreviada, denotar por
Vamos procurar soluções da forma
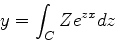 |
(934) |
onde 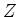 é uma função de
é uma função de 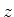 a determinar, e o contorno
a determinar, e o contorno 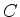 , independente
de
, independente
de 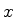 , também deve ser determinado. Como veremos, a determinação do
contorno é parte essencial na construção da solução, e aqui está talvez
a principal inovação dessa ``transformada de Laplace'' complexa.
Note-se que
, também deve ser determinado. Como veremos, a determinação do
contorno é parte essencial na construção da solução, e aqui está talvez
a principal inovação dessa ``transformada de Laplace'' complexa.
Note-se que
Como
temos,
ou
ou
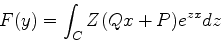 |
(935) |
com
e
Podemos então escrever 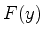 como uma soma de duas integrais:
como uma soma de duas integrais:
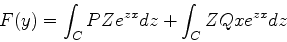 |
(936) |
A segunda dessas integrais pode ser escrita assim:
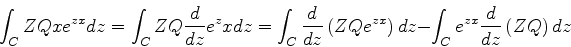 |
(937) |
Podemos agora escolher o contorno 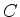 de tal sorte que a primeira integral
do segundo membro se anule. De fato, trata-se da integral de uma derivada;
logo, o valor da integral 'e a diferença dos valores do integrando nos dois
extremos. Escolhemos o contorno, então, ou como um contorno fechado, ou como
um contorno aberto em cujos dois extremos a função
de tal sorte que a primeira integral
do segundo membro se anule. De fato, trata-se da integral de uma derivada;
logo, o valor da integral 'e a diferença dos valores do integrando nos dois
extremos. Escolhemos o contorno, então, ou como um contorno fechado, ou como
um contorno aberto em cujos dois extremos a função
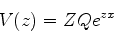 |
(938) |
tenha o mesmo valor (No caso do contorno fechado isto acontece
automaticamente). Com essa escolha de contorno,
Obtemos assim para a função 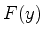 a expressão:
a expressão:
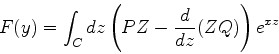 |
(939) |
Queremos determinar 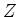 de tal forma que
de tal forma que 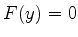 . Para tanto, o integrando
da Eq.(941) deve se anular. Assim,
. Para tanto, o integrando
da Eq.(941) deve se anular. Assim,
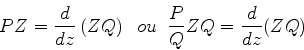 |
(940) |
o que nos leva à equação diferencial
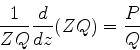 |
(941) |
Equivalentemente,
e
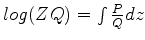 , ou ainda,
, ou ainda,
e, finalmente,
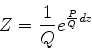 |
(942) |
A solução procurada é então
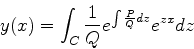 |
(943) |
ou, para maior clareza,
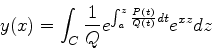 |
(944) |
onde 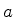 é, por exemplo, um dos zeros de
é, por exemplo, um dos zeros de 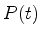 .
Considere a equação
.
Considere a equação
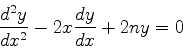 |
(945) |
que aparece na solução do problema de determinar os estados
estacionários do oscilador harmônico. Aqui  é um número qualquer,
não necessariamente um inteiro, apesar da notação. Colocando-a na forma
é um número qualquer,
não necessariamente um inteiro, apesar da notação. Colocando-a na forma
vemos que
Temos, então,
e
e, como
Logo,
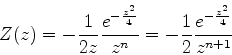 |
(946) |
e
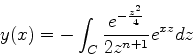 |
(947) |
Como estamos calculando uma função de onda, constantes multiplicativas
não têm importância. Por isso, simplificamos para
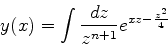 |
(948) |
Passemos agora à determinação do caminho de integração. Como vimos,
ele deve ser tal que a função 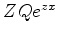 tenha o mesmo valor nos
dois extremos. Essa função é, neste caso,
tenha o mesmo valor nos
dois extremos. Essa função é, neste caso,
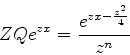 |
(949) |
Por argumentos físicos os casos de interesse
são restritos a
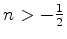 (Veja nota39). Para esses valores os contornos
(Veja nota39). Para esses valores os contornos
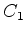 e
e 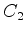 das figuras abaixo são adequados.
das figuras abaixo são adequados.
Seja 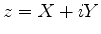 . O termo dominante no integrando é
. O termo dominante no integrando é
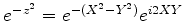 . Para
. Para 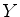 pequeno em módulo,
pequeno em módulo, 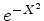 garante
que a função
garante
que a função 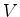 se anula nas extremidades de ambos os contornos.
se anula nas extremidades de ambos os contornos.
Se  for um racional não inteiro, a origem
for um racional não inteiro, a origem  será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que
será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que 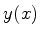 seja um polinômio,
como é requerido. Quando
seja um polinômio,
como é requerido. Quando  for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
onde introduzimos a nova variável complexa 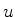 . Uma substituição simples
mostra que
. Uma substituição simples
mostra que
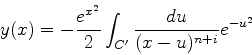 |
(950) |
onde o novo contorno 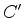 é descrito na figura abaixo.
é descrito na figura abaixo.
Que o contorno deve ser este, segue dos seguintes fatos:a transformação é
linear; uma transformação linear transforma retas em retas e círculos
em círculos40; a particular transformação acima inverte o sentido de
percurso no contorno e leva pequenos valores da parte imaginária de 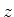 em pequenos valores da parte imaginária de
em pequenos valores da parte imaginária de 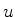 ; o ponto
; o ponto  corresponde
ao ponto
corresponde
ao ponto 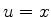 no novo contorno.
no novo contorno.
Para  inteiro e
inteiro e  o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para
o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para
A integral é, então,
 |
(951) |
Ora,
onde usamos a fórmula de Cauchy. Portanto,
 |
(952) |
Mas, uma maneira de definir os polinômios de Hermite é:
Logo,
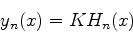 |
(953) |
onde 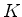 é uma constante arbitrária, a ser determinada posteriormente
pela normalização da função de onda.
Nada supera em importância, na gênese da mecânica Newtoniana,
o problema da queda livre, seja da maçã, seja da Lua, em seu
movimento em redor da Terra. No entanto raramente se vê, num
curso de mecânica quântica, esses problemas tratados, nem mesmo
no caso simplificado de um campo gravitacional constante. Nesta secção
vamos resolver o problema do movimento de um ponto material sob a
ação de um campo uniforme: a queda da maçã, se a altura da queda
não for muito grande. O método de Laplace para resolver a equação
diferencial obtida será essencial.
é uma constante arbitrária, a ser determinada posteriormente
pela normalização da função de onda.
Nada supera em importância, na gênese da mecânica Newtoniana,
o problema da queda livre, seja da maçã, seja da Lua, em seu
movimento em redor da Terra. No entanto raramente se vê, num
curso de mecânica quântica, esses problemas tratados, nem mesmo
no caso simplificado de um campo gravitacional constante. Nesta secção
vamos resolver o problema do movimento de um ponto material sob a
ação de um campo uniforme: a queda da maçã, se a altura da queda
não for muito grande. O método de Laplace para resolver a equação
diferencial obtida será essencial.
Uma partícula de massa  (a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo
(a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo 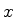 , o que lhe dá uma energia potencial
, o que lhe dá uma energia potencial
Logo, age sobre ela uma força na direção 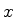 , de módulo
, de módulo 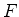 . O
movimento da partícula é também restrito (por escolha das
condições iniciais) ao eixo
. O
movimento da partícula é também restrito (por escolha das
condições iniciais) ao eixo 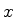 .
.
A equação de Schrödinger para os estados estacionários desse
sistema é:
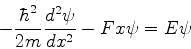 |
(954) |
ou
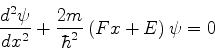 |
(955) |
É conveniente introduzir a variável adimensional
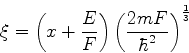 |
(956) |
Temos então
e, após algumas substituições simples,
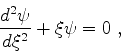 |
(957) |
como nova equação de Schrödinger .
Trata-se de uma equação de Laplace. Na notação convencional, temos
 |
(958) |
à qual o método que vimos acima pode ser aplicado. Contudo, para
aproveitar os estudos prévios sobre uma função que irá aparecer
no problema (a função de Airy), vamos estudar não a equação acima,
mas uma estreitamente ligada a ela,
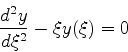 |
(959) |
que é muito conhecida na física-matemática. Se 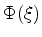 for
solução desta equação,
for
solução desta equação, 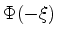 será solução da Eq.(959).
A Eq.(961) é escrita, à maneira de Laplace, assim:
será solução da Eq.(959).
A Eq.(961) é escrita, à maneira de Laplace, assim:
 |
(960) |
com 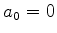 ,
, 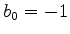 ,
, 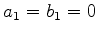 ,
, 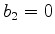 ,
, 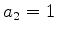 . Segue que
. Segue que
e, como
 ,
,
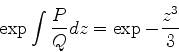 |
(961) |
e então
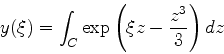 |
(962) |
Como vimos, o contorno de integração deve ser escolhido de maneira
que a função
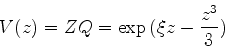 |
(963) |
tenha valores idênticos nos dois extremos. Neste caso tomaremos
um contorno que vai ao infinito, sendo os valores de 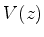 nos
dois extremos iguais a zero.
Seja
nos
dois extremos iguais a zero.
Seja  . Então
. Então
O contorno deve ser tal que a exponencial leve o integrando a zero nos
dois extremos. Para isso, devemos ter:
Consideremos primeiro o caso  . Devemos então ter
. Devemos então ter
Esta é uma região do plano 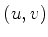 delimitada pelas retas
delimitada pelas retas
e
Na figura abaixo estão representadas essas duas retas. Sobre elas temos
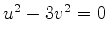 . Uma pequena reflexão com ajuda da figura convencerá o leitor
de que a região entre as retas é aquela em que
. Uma pequena reflexão com ajuda da figura convencerá o leitor
de que a região entre as retas é aquela em que 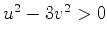 . A região
. A região 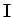 é aquela em que temos
é aquela em que temos 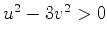 e
e  . A região simétrica
à tracejada em relação ao eixo
. A região simétrica
à tracejada em relação ao eixo 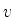 , isto é, a região
, isto é, a região 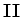 ,
é aquela em que temos
,
é aquela em que temos 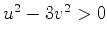 e
e
 . Logo, a região em que
. Logo, a região em que 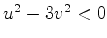 e
e  é a complementar dessa
região
é a complementar dessa
região 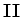 no semiplano que contém o eixo real negativo,
e é constituída pelas regiões
no semiplano que contém o eixo real negativo,
e é constituída pelas regiões  e
e
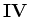 . Essas regiões estendem-se ao infinito, embora isto
não seja (nem possa ser!) representado na figura. Em princípio o
contorno de integração pode começar em qualquer das regiões tracejadas,
e terminar em qualquer outra tracejada.
. Essas regiões estendem-se ao infinito, embora isto
não seja (nem possa ser!) representado na figura. Em princípio o
contorno de integração pode começar em qualquer das regiões tracejadas,
e terminar em qualquer outra tracejada.
Na figura estão indicados, em cinza, três contornos
possíveis: 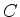 ,
, 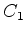 e
e 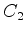 .
Desses,
.
Desses, 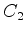 é problemático, pois se estende na região
em que a variável
é problemático, pois se estende na região
em que a variável 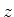 atinge valores reais e positivos. Então o termo
atinge valores reais e positivos. Então o termo
que aparece na expressão de 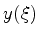 , pode, para
, pode, para 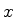 grande e positivo,
complicar a convergência da integral. Por isso tomamos os contornos
que começam na região
grande e positivo,
complicar a convergência da integral. Por isso tomamos os contornos
que começam na região 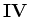 e terminam na
e terminam na  .
Em particular, o caminho
.
Em particular, o caminho 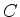 pode ser ao longo do eixo imaginário.
Então, tomando
pode ser ao longo do eixo imaginário.
Então, tomando 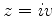 ,
,
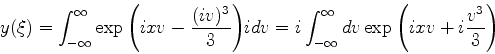 |
(964) |
ou
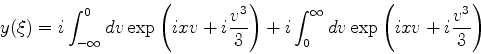 |
(965) |
ou ainda
e, finalmente,
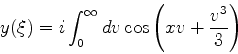 |
(966) |
A função de Airy, bem conhecida na literatura matemática,
é definida por
 |
(967) |
Logo,
 |
(968) |
As funções descritas pelas Eqs.(969) e (970)
estão expressas como uma representação integral, e, sendo assim,
não se pode ter uma idéia imediata de seu comportamento. Nos casos
em que
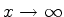 e
e
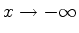 obtêm-se
comportamentos assintóticos mais reveladores. Vamos a eles.
obtêm-se
comportamentos assintóticos mais reveladores. Vamos a eles.
Para 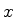 positivo e muito grande na função de Airy (correspondendo
a
positivo e muito grande na função de Airy (correspondendo
a 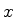 negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
É conveniente voltar à expressão exponencial
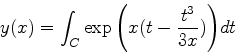 |
(969) |
Pondo
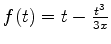 temos
temos
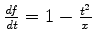 e a condição
e a condição
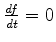 implica em
implica em 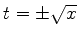 , que são
os possíveis pontos sela. Na região permitida, temos só o valor
, que são
os possíveis pontos sela. Na região permitida, temos só o valor
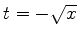 . A seguir faremos a escolha de um caminho de integração
que passe pelo ponto sela e seja de máximo aclive. Na realidade,
é suficiente que o caminho seja de máximo aclive nas
vizinhanças do ponto sela. Vamos então expandir
. A seguir faremos a escolha de um caminho de integração
que passe pelo ponto sela e seja de máximo aclive. Na realidade,
é suficiente que o caminho seja de máximo aclive nas
vizinhanças do ponto sela. Vamos então expandir 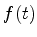 em
série de Taylor em torno de
em
série de Taylor em torno de 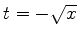 . Temos,
. Temos,
as derivadas sendo calculadas no ponto 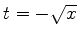 . Facilmente se
obtém que
. Facilmente se
obtém que
e que
Naturalmente a derivada primeira é zero nesse ponto, pois ele é
ponto sela. Então,
 |
(970) |
Para separar as partes real e imaginária de 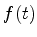 escrevo
escrevo
o que dá
Então, nas vizinhanças de 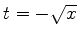 , temos:
, temos:
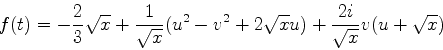 |
(971) |
Considere a reta 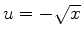 . Ao longo dela,
. Ao longo dela, 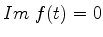 . Logo,
é uma curva de máximo aclive.
. Logo,
é uma curva de máximo aclive.
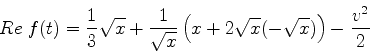 |
(972) |
ou, simplificando,
 |
(973) |
Então a linha de maior aclive é a paralela ao eixo imaginário
passando por 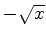 . Pondo
. Pondo
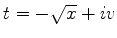 , temos
, temos
 |
(974) |
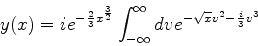 |
(975) |
e podemos omitir a exponencial imaginária do integrando, pois
a parte gaussiana, para grandes valores de 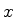 , restringe de tal
forma o trecho do contorno que conta para a integral, que
, restringe de tal
forma o trecho do contorno que conta para a integral, que
 pode ser substituída por seu valor em
pode ser substituída por seu valor em 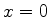 .
Então,
.
Então,
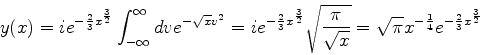 |
(976) |
Levando em conta a definição da função de Airy, temos o comportamento
assintótico
 |
(977) |
Como a função de onda do sistema sob a ação do campo uniforme é
o comportamento assintótico que obtivemos é o esperado, uma vez que,
para 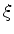 negativo e de grande módulo, estamos na região classicamente
inacessível, e a exponencial negativa é bem-vinda.
negativo e de grande módulo, estamos na região classicamente
inacessível, e a exponencial negativa é bem-vinda.
Consideremos agora o comportamento assintótico para grandes valores
de 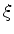 , o que corresponde, na função de Airy, a
, o que corresponde, na função de Airy, a 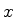 negativo e de
frande módulo. Neste caso
negativo e de
frande módulo. Neste caso
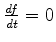 dá
dá
ou seja, 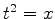 , com
, com 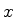 negativo. Então,
negativo. Então,
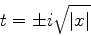 |
(978) |
Aqui os dois pontos sela devem ser considerados, já que estão,
ambos, em regiões onde a integral converge. Vamos, primeiro,
ao ponto 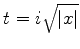 . Expandindo a função
. Expandindo a função
 em torno do ponto sela, temos:
em torno do ponto sela, temos:
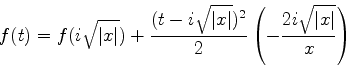 |
(979) |
onde omitimos o termo contendo a derivada primeira, já que ela se anula
no ponto sela. Após um cálculo simples, obtém-se:
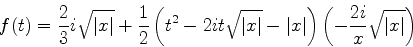 |
(980) |
Usando 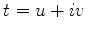 ,
,
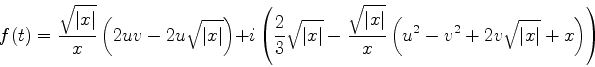 |
(981) |
Segue que
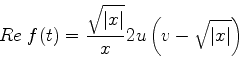 |
(982) |
e
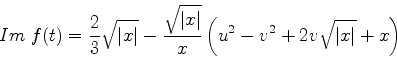 |
(983) |
ou
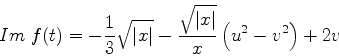 |
(984) |
Ao longo da reta
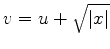 temos
temos
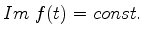 , logo, este
é o primeiro trecho do caminho, aquele que passa pelo ponto sela
, logo, este
é o primeiro trecho do caminho, aquele que passa pelo ponto sela
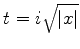 .
.
Considerações inteiramente análogas levam à conclusão que o
segundo trecho do contorno é a reta
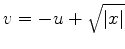 , ou, mais
precisamente, o segmento que começa no eixo real, em
, ou, mais
precisamente, o segmento que começa no eixo real, em 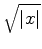 e
vai a
e
vai a 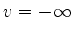 . Assim, o contorno de integração adequado para o
comportamento assintótico para
. Assim, o contorno de integração adequado para o
comportamento assintótico para 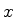 negativo e de grande módulo
é o que está representado na figura abaixo.
negativo e de grande módulo
é o que está representado na figura abaixo.
A contribuição do trecho superior do contorno à integral é:
Alguma álgebra elementar leva este resultado à forma:
 |
(989) |
onde pusemos 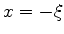 .
A contribuição do outro trecho é perfeitamente análoga, dando como resultado
.
A contribuição do outro trecho é perfeitamente análoga, dando como resultado
 |
(990) |
Somando as duas, temos
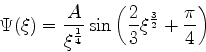 |
(991) |
Vamos nos deter agora um pouco na interpretação física do
resultado, comparando a solução com a solução clássica para o mesmo
problema. É preciso ressaltar que o que calculamos foram as funções
de onda dos estados estacionários de um corpo sob a ação
de uma força constante (queda livre, por exemplo). Classicamente
nunca, ou raramente, estudamos estados estacionários, o que
torna a comparação entre os resultados mais dificil. Para realizar
estados estacionários em queda livre na mecânica clássica, temos
que recorrer a um conjunto de muitas partículas. Um bom modelo de
queda livre em estado estacionário na mecânica clássica é
uma cachoeira sem turbulência, um lençol homogêneo de água
em queda livre. Cada gota de água estará em movimento, mas
o conjunto de todas as gotas forma uma figura que, no conjunto,
parece imóvel. Vamos mostrar que a solução quântica que obtivemos
possui algo em comum com a solução clássica. Isto é mais fácil
de ver usando-se a expressão assintótica
da Eq.(993).
De fato, usando a Eq.(993) temos que
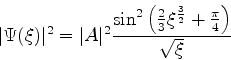 |
(992) |
O sistema clássico correspondente é uma partícula de massa  em queda livre (ou, antes, uma enorme quantidade delas). A conservação
da energia dá
em queda livre (ou, antes, uma enorme quantidade delas). A conservação
da energia dá
 |
(993) |
de onde se tira
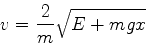 |
(994) |
e, portanto,
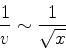 |
(995) |
Para o sistema clássico, a probabilidade de se encontrar a
partícula
em torno de uma posição 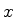 é inversamente proporcional à velocidade dela
naquela posição, pois é diretamente proporcional ao tempo que a
partícula em torno da posição. Quanticamente esta probabilidade é
dada
por
é inversamente proporcional à velocidade dela
naquela posição, pois é diretamente proporcional ao tempo que a
partícula em torno da posição. Quanticamente esta probabilidade é
dada
por 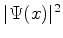 . Comparando a Eq.(994) com a
Eq.(997), vemos que a dependência em
. Comparando a Eq.(994) com a
Eq.(997), vemos que a dependência em  comparece nas duas.
comparece nas duas.
Seja
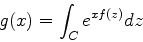 |
(996) |
onde 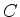 é um contorno aberto com a propriedade de que
é um contorno aberto com a propriedade de que
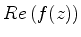 tenda a
tenda a  em ambas as suas extremidades. A partir de agora
escreveremos o número complexo
em ambas as suas extremidades. A partir de agora
escreveremos o número complexo 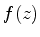 assim, decomposto em sua parte
real e imaginária:
assim, decomposto em sua parte
real e imaginária:
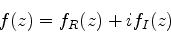 |
(997) |
Consideremos valores positivos e grandes de 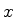 . Como
. Como
e
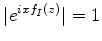 , o módulo do integrando na Eq.(998)
é dado por
, o módulo do integrando na Eq.(998)
é dado por 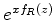 . Esta função, para um dado
. Esta função, para um dado 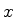 , varia de um valor
máximo, atingido quando
, varia de um valor
máximo, atingido quando  é máximo, até zero, pelo menos nos
extremos. Para
é máximo, até zero, pelo menos nos
extremos. Para 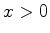 e muito grande, temos um ``pico'' muito elevado, de
onde o valor da integral cai rapidamente para o ``vale'' (região de baixos
valores). Além disso, podemos utilizar a possibilidade de deformar o
contorno, para fazer com que ele fique ``a maior parte do tempo'' nos vales,
subindo ao pico pelo caminho mais íngreme. Desta maneira, apenas uma pequena
parte do contorno contribuirá efetivamente para a integral. O método do
ponto sela é isto: achar o contorno mais íngreme, passando pelo pico. Note
que são os valores muito grandes de
e muito grande, temos um ``pico'' muito elevado, de
onde o valor da integral cai rapidamente para o ``vale'' (região de baixos
valores). Além disso, podemos utilizar a possibilidade de deformar o
contorno, para fazer com que ele fique ``a maior parte do tempo'' nos vales,
subindo ao pico pelo caminho mais íngreme. Desta maneira, apenas uma pequena
parte do contorno contribuirá efetivamente para a integral. O método do
ponto sela é isto: achar o contorno mais íngreme, passando pelo pico. Note
que são os valores muito grandes de 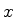 que acentuam essas propriedades
extremas. Logo, o método se presta para calcular valores assintóticos.
que acentuam essas propriedades
extremas. Logo, o método se presta para calcular valores assintóticos.
A determinação do caminho mais íngreme passando pelo pico pode ser feita
assim: considere as curvas de nível de  , ou seja, as curvas
ao longo das quais
, ou seja, as curvas
ao longo das quais  é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais
é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais 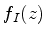 é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
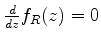 . Vimos agora que, pelo caminho escolhido,
. Vimos agora que, pelo caminho escolhido,
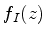 é constante, e, portanto,
é constante, e, portanto,
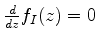 . Logo, o
ponto sela satisfaz a equação complexa
. Logo, o
ponto sela satisfaz a equação complexa
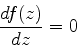 |
(998) |
Seja 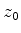 o ponto em que essa equação é satisfeita (pode haver vários).
Expandindo a função em torno desse ponto, temos
o ponto em que essa equação é satisfeita (pode haver vários).
Expandindo a função em torno desse ponto, temos
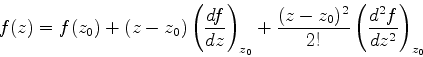 |
(999) |
mais termos de ordem superior. A derivada primeira é nula, por definição
de ponto sela. Logo, temos, para a parte real do integrando,
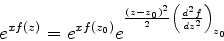 |
(1000) |
com
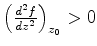 , ao longo do
contorno, por ser um máximo de
, ao longo do
contorno, por ser um máximo de  . Logo,
. Logo,
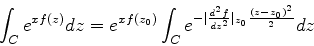 |
(1001) |
que, em geral, por ser a integral de uma gaussiana, pode ser calculada
facilmente.
Considere a função
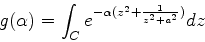 |
(1002) |
onde o contorno 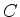 , ilustrado na figura, começa e termina no eixo
real, em
, ilustrado na figura, começa e termina no eixo
real, em  e
e 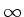 , respectivamente.
A função é da forma
, respectivamente.
A função é da forma
com 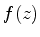 dada por
dada por
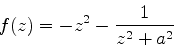 |
(1003) |
Um cálculo simples mostra que
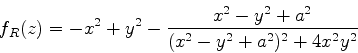 |
(1004) |
enquanto que
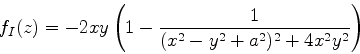 |
(1005) |
Como a integral converge, já que  tende a zero para
tende a zero para
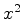 tendendo a infinito com
tendendo a infinito com 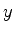 limitado, as singularidades de
limitado, as singularidades de
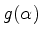 são as singularidades do integrando. A função
são as singularidades do integrando. A função 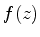 tem polos em
tem polos em 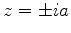 . O contorno
. O contorno 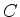 está entre
está entre 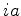 e o eixo
real. Logo, podemos deformá-lo a vontade nessa região.
e o eixo
real. Logo, podemos deformá-lo a vontade nessa região.
O ponto sela é determinado pela equação
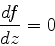 |
(1006) |
ou seja,
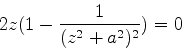 |
(1007) |
que tem a solução
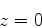 |
(1008) |
A derivada segunda de 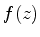 é
é
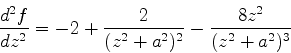 |
(1009) |
e, no ponto sela, tem o valor
 |
(1010) |
A família de curvas 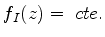 é muito complicada. No entanto,
para a curva
é muito complicada. No entanto,
para a curva 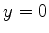 com
com 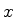 qualquer, temos
qualquer, temos 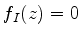 , e, portanto,
constante. Como esta curva passa por
, e, portanto,
constante. Como esta curva passa por  , ela é a curva de máximo
aclive procurada. Ou seja, para o cálculo do valor assintótico
de
, ela é a curva de máximo
aclive procurada. Ou seja, para o cálculo do valor assintótico
de 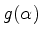 é conveniente deformar o contorno de maneira a fazê-lo
coincidir com o eixo real. Portanto, temos
é conveniente deformar o contorno de maneira a fazê-lo
coincidir com o eixo real. Portanto, temos
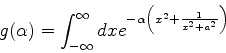 |
(1011) |
Podemos agora expandir 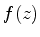 em torno do ponto sela. Como
a derivada primeira é nula no ponto sela, resulta que
em torno do ponto sela. Como
a derivada primeira é nula no ponto sela, resulta que
 |
(1012) |
o que dá
 |
(1013) |
Temos então para 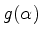 :
:
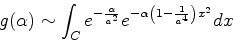 |
(1014) |
e agora a integral pode ser calculada facilmente. De fato,
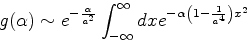 |
(1015) |
Usando o resultado conhecido ( integral de Gauss)
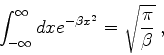 |
(1016) |
obtemos
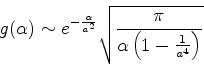 |
(1017) |
que é o resultado procurado, válido para grandes valores de
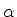 .
.
Henrique Fleming 2003
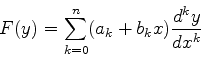
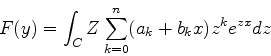
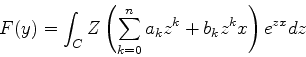

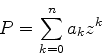
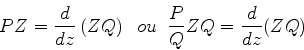
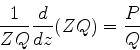
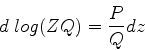

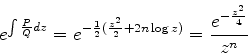
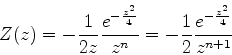
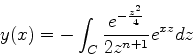
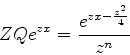
![]() for um racional não inteiro, a origem
for um racional não inteiro, a origem ![]() será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que
será um ponto de
ramificação, e haverá cortes ao longo do eixo real. Se o corte for
tomado ao longo do semi-eixo real negativo, o primeiro contorno não é
permitido (a curva atravessa o corte). O segundo é aceitável. A
integração é complicada, e não garante que ![]() seja um polinômio,
como é requerido. Quando
seja um polinômio,
como é requerido. Quando ![]() for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
for inteiro, a situação é muito mais simples.
Façamos, neste caso, a mudança de variável
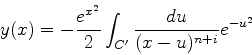
![]() em pequenos valores da parte imaginária de
em pequenos valores da parte imaginária de ![]() ; o ponto
; o ponto ![]() corresponde
ao ponto
corresponde
ao ponto ![]() no novo contorno.
no novo contorno.
![]() inteiro e
inteiro e ![]() o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para
o integrando não tem singularidades. Por isso,
o contorno pode ser deformado para

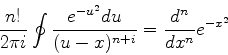
![]() (a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo
(a ``maçã'')se move sob a ação de um
campo uniforme
ao longo do eixo ![]() , o que lhe dá uma energia potencial
, o que lhe dá uma energia potencial
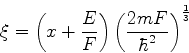
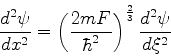


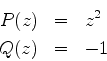
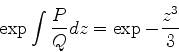
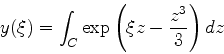

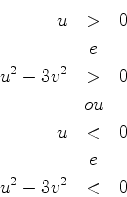
![\begin{pspicture}(0,0)(10,6)
\psline[linewidth=2pt]{->}(0,3)(10,3)
\psline[lin...
...gray]{->}(2,0)(3,1.5)(5.7,3)(9.3,4)
\uput[0](7.5,4){$\bf C_2$}
\end{pspicture}](img2726.png)
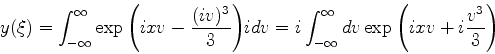
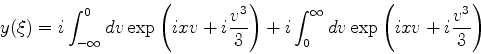
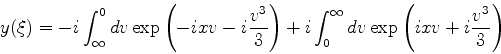
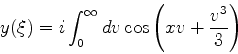
![]() positivo e muito grande na função de Airy (correspondendo
a
positivo e muito grande na função de Airy (correspondendo
a ![]() negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
negativo e de módulo muito grande para a função de onda)
temos de achar um contorno de integração que permita utilizar
o método do ponto sela. (Veja o Apêndice dedicado a este
método).
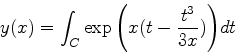
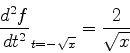

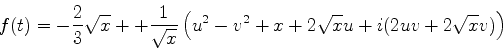
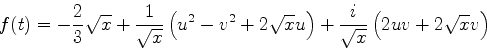
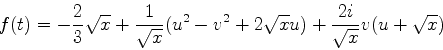
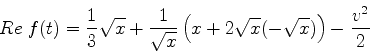

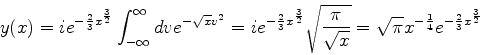
![]() , o que corresponde, na função de Airy, a
, o que corresponde, na função de Airy, a ![]() negativo e de
frande módulo. Neste caso
negativo e de
frande módulo. Neste caso
![]() dá
dá
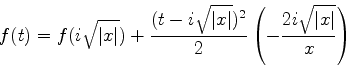
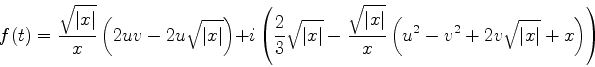
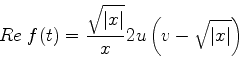
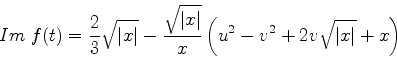
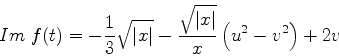
![]() , ou, mais
precisamente, o segmento que começa no eixo real, em
, ou, mais
precisamente, o segmento que começa no eixo real, em ![]() e
vai a
e
vai a ![]() . Assim, o contorno de integração adequado para o
comportamento assintótico para
. Assim, o contorno de integração adequado para o
comportamento assintótico para ![]() negativo e de grande módulo
é o que está representado na figura abaixo.
negativo e de grande módulo
é o que está representado na figura abaixo.
{$-i\sqrt{\vert x\vert}$}
\end{pspicture}](img2781.png)
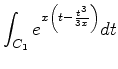
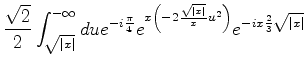
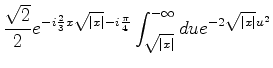
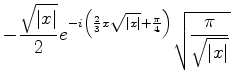



![]() , ou seja, as curvas
ao longo das quais
, ou seja, as curvas
ao longo das quais ![]() é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais
é constante. O que procuramos são as curvas
que cortem essas curvas de nível ortogonalmente: são estas as que
``sobem mais rapidamente''. Ora, essas curvas são, como se sabe da
teoria de funções analíticas de uma variável complexa, as curvas ao
longo das quais ![]() é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
é constante. Logo, temos de achar a curva
dessa família que passa pelo ``pico''. No ``pico'' (que é o ponto
sela) temos
![]() . Vimos agora que, pelo caminho escolhido,
. Vimos agora que, pelo caminho escolhido,
![]() é constante, e, portanto,
é constante, e, portanto,
![]() . Logo, o
ponto sela satisfaz a equação complexa
. Logo, o
ponto sela satisfaz a equação complexa
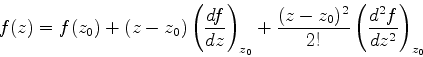
{$ia$}
\psdots[dotstyle=*](5,5.5)
\end{pspicture}](img2815.png)