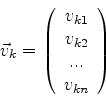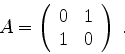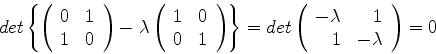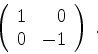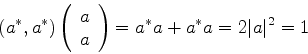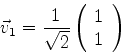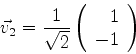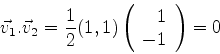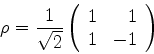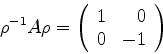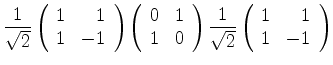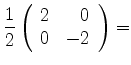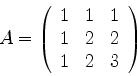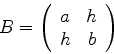Subsections
Seja  um operador linear num espaço vetorial
um operador linear num espaço vetorial 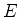 sobre os números complexos. Seja
sobre os números complexos. Seja 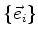 , com
, com
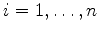 , uma base desse espaço, que, portanto, tem dimensão
, uma base desse espaço, que, portanto, tem dimensão
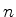 . Aplicando-se
. Aplicando-se  a um elemento da base, por exemplo,
a um elemento da base, por exemplo, 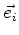 ,
tem-se um novo vetor do espaço, que pode ser expandido na base
dada. Esta expansão é escrita
,
tem-se um novo vetor do espaço, que pode ser expandido na base
dada. Esta expansão é escrita
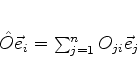 |
(868) |
onde os 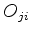 são números complexos, denominados elementos
de matriz de
são números complexos, denominados elementos
de matriz de  na base
na base 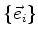 .
.
Seja 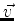 um vetor qualquer de
um vetor qualquer de 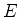 , tal que
, tal que
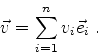 |
(869) |
Temos
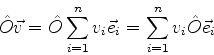 |
(870) |
e, usando (869),
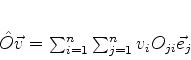 |
(871) |
A equação (872) mostra que, de posse dos elementos de
matriz de  , é possível determinar a ação deste operador
sobre qualquer vetor. Ou seja, escolhida uma base, o operador pode
ser substituído pelo conjunto de seus elementos de matriz. Convenciona-se
escrever o conjunto desses elementos de matriz da seguinte forma:
, é possível determinar a ação deste operador
sobre qualquer vetor. Ou seja, escolhida uma base, o operador pode
ser substituído pelo conjunto de seus elementos de matriz. Convenciona-se
escrever o conjunto desses elementos de matriz da seguinte forma:
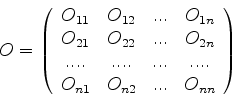 |
(872) |
Uma segunda maneira de ler a eq.(872) é : as componentes
do vetor
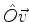 em relação à base dada são os números
complexos
em relação à base dada são os números
complexos
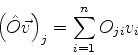 |
(873) |
Se representarmos os vetores por matrizes coluna cujos elementos são as
suas componentes,
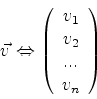 |
(874) |
podemos representar a ação de um operador sobre um vetor assim:
 |
(875) |
onde, para calcular o segundo membro, usam-se as regras de produtos de
matrizes usuais.
O leitor, como exercício, poderá mostrar que a representação matricial
do operador
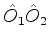 , produto dos operadores
, produto dos operadores 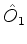 e
e
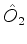 , é dada pelo produto, no sentido de matrizes, das matrizes que
representam
, é dada pelo produto, no sentido de matrizes, das matrizes que
representam 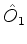 e
e 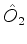 , nesta ordem. Recordemos que o produto
das matrizes
, nesta ordem. Recordemos que o produto
das matrizes 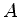 , de elementos
, de elementos 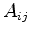 e
e 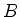 , de elementos
, de elementos 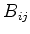 , é a
matriz de elementos
, é a
matriz de elementos
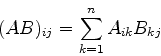 |
(876) |
regra que pode ser obtida facilmente da equação (869).
Seja 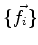 uma segunda base. Podemos escrever
uma segunda base. Podemos escrever
 |
(877) |
enquanto que, em relação à primeira (para o mesmo  )
)
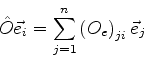 |
(878) |
onde indicamos com 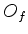 e
e 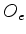 as matrizes que representam
as matrizes que representam  nas bases
nas bases 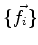 e
e 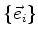 respectivamente.
As matrizes
respectivamente.
As matrizes 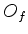 e
e 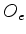 representam o mesmo operador em bases distintas.
Matrizes com esta propriedades são ditas equivalentes. O que
caracteriza matrizes equivalentes?
Um elemento qualquer da base (f) pode ser expandido na base (e):
representam o mesmo operador em bases distintas.
Matrizes com esta propriedades são ditas equivalentes. O que
caracteriza matrizes equivalentes?
Um elemento qualquer da base (f) pode ser expandido na base (e):
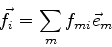 |
(879) |
e analogamente,
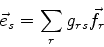 |
(880) |
Logo, segue que
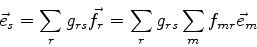 |
(881) |
ou
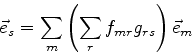 |
(882) |
de onde segue, imediatamente, que
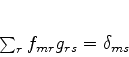 |
(883) |
Invertendo os papeis das bases (e) e (f), obtém-se, da mesma maneira,
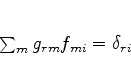 |
(884) |
Seja 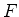 a matriz cujos elementos são
a matriz cujos elementos são 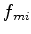 , e
, e
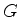 aquela cujos elementos são
aquela cujos elementos são 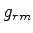 . Então as equações
(884) e (885) são escritas, respectivamente,
. Então as equações
(884) e (885) são escritas, respectivamente,
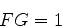 |
(885) |
e
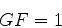 |
(886) |
Quando, entre duas matrizes, existe este par de relações, uma é o inverso
da outra. Ou seja,
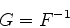 |
(887) |
ou, equivalentemente,
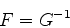 |
(888) |
A condição necessária e suficiente para que uma matriz tenha inverso
é que seu determinante seja diferente de zero.
Sejam 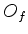 e
e 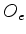 duas representações matriciais do operador
duas representações matriciais do operador
 , ou seja, duas matrizes equivalentes. Temos
, ou seja, duas matrizes equivalentes. Temos
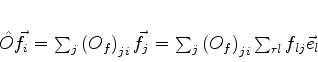 |
(889) |
Por outro lado,
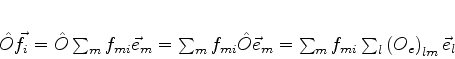 |
(890) |
Igualando (890) e (891), temos
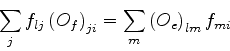 |
(891) |
ou, na linguagem das matrizes,
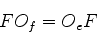 |
(892) |
ou, na forma mais comum,
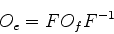 |
(893) |
Em palavras, duas matrizes 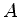 e
e 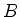 são equivalentes se existir
uma matriz não-singular (isto é, que tem inversa)
são equivalentes se existir
uma matriz não-singular (isto é, que tem inversa) 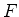 tal que
tal que
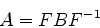 |
(894) |
Uma relação desse tipo entre matrizes 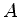 e
e 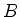 é dita também uma
transformação de eqüivalência, ou de semelhança. A riqueza de sinônimos
revela a idade do problema!
é dita também uma
transformação de eqüivalência, ou de semelhança. A riqueza de sinônimos
revela a idade do problema!
Sejam  um operador linear e
um operador linear e
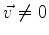 um vetor tais que
um vetor tais que
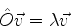 |
(895) |
onde 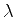 é um número complexo. Diz-se que
é um número complexo. Diz-se que 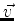 é um autovetor
de
é um autovetor
de  , e que
, e que 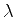 é um autovalor de
é um autovalor de  .
A equação acima pode ser escrita assim:
.
A equação acima pode ser escrita assim:
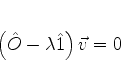 |
(896) |
Suponhamos que o operador
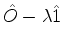 tenha inverso, denotado
por
tenha inverso, denotado
por
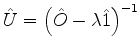 . Então, aplicando-se
. Então, aplicando-se
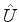 à esquerda de (897), temos
à esquerda de (897), temos
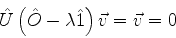 |
(897) |
o que é absurdo, pois 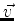 , como autovetor, deve ser não-nulo.
Conclui-se que o operador
, como autovetor, deve ser não-nulo.
Conclui-se que o operador
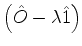 é singular,
ou seja, não tem inverso. Em conseqüência, suas representações matriciais
também não terão inverso.
é singular,
ou seja, não tem inverso. Em conseqüência, suas representações matriciais
também não terão inverso.
A versão matricial da eq.(897) é
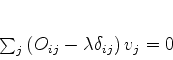 |
(898) |
onde 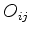 é o elemento
é o elemento 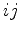 da matriz
da matriz 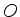 , que representa o operador
, que representa o operador
 em alguma base, e
em alguma base, e 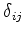 é o elemento
é o elemento 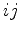 da matriz
que representa o operador
da matriz
que representa o operador 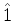 . Em conseqüência da conclusão acima,
o primeiro membro da eq.(899) deve ser uma matriz singular
(sem inverso). Logo, devemos ter
. Em conseqüência da conclusão acima,
o primeiro membro da eq.(899) deve ser uma matriz singular
(sem inverso). Logo, devemos ter
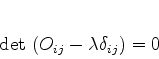 |
(899) |
que é uma maneira simplificada de dizer que o determinante da matriz cujo
elemento genérico é
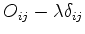 é zero.
é zero.
Esta equação, 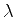 sendo a incógnita, é uma equação algébrica
de ordem igual à dimensão
sendo a incógnita, é uma equação algébrica
de ordem igual à dimensão 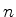 do espaço, ou, o que é o mesmo,
igual à ordem da matriz. Em prinípio tem
do espaço, ou, o que é o mesmo,
igual à ordem da matriz. Em prinípio tem 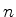 soluções, mas não
necessariamente distintas. Estas soluções são os autovalores do operador,
e são também chamadas de autovalores da matriz que representa o operador.
A equação (900) é conhecida como equação secular.
soluções, mas não
necessariamente distintas. Estas soluções são os autovalores do operador,
e são também chamadas de autovalores da matriz que representa o operador.
A equação (900) é conhecida como equação secular.
Seja 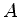 uma matriz, de elementos
uma matriz, de elementos 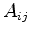 , que são números
complexos. Seja
, que são números
complexos. Seja 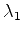 um autovalor da matriz
um autovalor da matriz 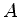 . Isto quer dizer que existe
. Isto quer dizer que existe
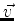 tal que36
tal que36
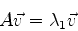 |
(900) |
ou
Mais geralmente, seja 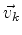 o autovetor correspondente ao
autovalor
o autovetor correspondente ao
autovalor 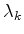 ,
,
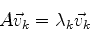 |
(902) |
Escrevendo a relação acima em componentes, temos
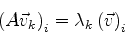 |
(903) |
ou
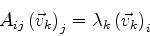 |
(904) |
Considere a matriz cujos elementos são
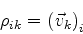 |
(905) |
Então
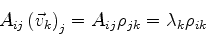 |
(906) |
ou, definindo a matriz diagonal 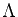 , de elementos
, de elementos
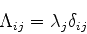 |
(907) |
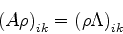 |
(908) |
ou, como uma equação matricial,
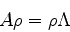 |
(909) |
Se a matriz 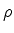 for inversível, isto é, se existir
for inversível, isto é, se existir 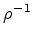 ,
obtemos, aplicando
,
obtemos, aplicando 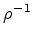 à esquerda,
à esquerda,
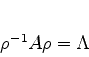 |
(910) |
A matriz 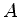 foi transformada, por uma ``transformação de semelhança'',
numa matriz diagonal. Seja
foi transformada, por uma ``transformação de semelhança'',
numa matriz diagonal. Seja 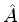 o operador linear que, em relação a uma
determinada base, possui a representação matricial
o operador linear que, em relação a uma
determinada base, possui a representação matricial 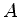 . A equação (911)
mostra que, no caso de
. A equação (911)
mostra que, no caso de 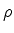 possuir inversa, existe uma outra base
na qual
possuir inversa, existe uma outra base
na qual 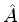 é representado pela matriz diagonal
é representado pela matriz diagonal 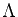 .
.
Que matriz é 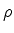 ? Sejam
? Sejam
os autovetores de 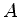 , para
, para 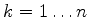 . Seja a matriz construída justapondo-se
essas matrizes colunas designada por
. Seja a matriz construída justapondo-se
essas matrizes colunas designada por 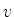 . Então
. Então
 |
(911) |
A matriz 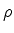 é a transposta de
é a transposta de 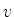 , ou seja,
, ou seja,
 |
(912) |
Condição necessária e suficiente para que exista 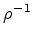 é que o determinante de
é que o determinante de 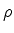 seja diferente de zero. Ora,
uma condição suficiente para que o determinante de uma matriz
seja não-nulo é que suas linhas sejam linearmente independentes.
Como as linhas de
seja diferente de zero. Ora,
uma condição suficiente para que o determinante de uma matriz
seja não-nulo é que suas linhas sejam linearmente independentes.
Como as linhas de 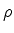 são os autovetores
são os autovetores 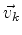 , conclui-se
que uma condição suficiente para que exista
, conclui-se
que uma condição suficiente para que exista 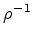 é que
os autovetores de
é que
os autovetores de 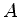 sejam linearmente independentes. Um corolário
é que, se
sejam linearmente independentes. Um corolário
é que, se 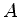 é hermiteana, ela é diagonalizavel, pois o conjunto
dos autovetores de uma matriz hermiteana forma uma base, o que significa
que os autovetores são linearmente independentes.
Diagonalizar a matriz complexa37
é hermiteana, ela é diagonalizavel, pois o conjunto
dos autovetores de uma matriz hermiteana forma uma base, o que significa
que os autovetores são linearmente independentes.
Diagonalizar a matriz complexa37
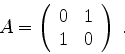 |
(913) |
A equação secular (900) é, neste caso,
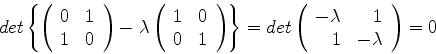 |
(914) |
ou
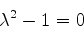 |
(915) |
cujas soluções são
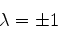 |
(916) |
Então a matriz, quando estiver na forma diagonal, será
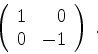 |
(917) |
Contudo, vamos construir explicitamente a transformação de
semelhança que leva 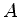 à forma diagonal. Para isso
precisamos determinar os autovetores de
à forma diagonal. Para isso
precisamos determinar os autovetores de 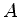 . Seus autovalores
já foram determinados: são
. Seus autovalores
já foram determinados: são
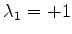 e
e
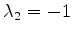 . Temos
Seja
. Temos
Seja 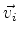 o autovetor associado ao autovalor
o autovetor associado ao autovalor 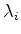 . Então,
. Então,
Denotando o vetor 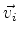 pela matriz coluna
pela matriz coluna
temos, para (920):
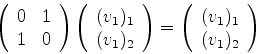 |
(920) |
Realizando o produto de matrizes do primeiro termo, temos
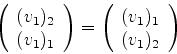 |
(921) |
Como a igualdade de matrizes implica na igualdade, um a um,
dos termos de mesmos índices, temos
A solução mais geral dessas equações é a matriz coluna
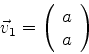 |
(924) |
onde 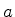 é qualquer número diferente de zero. Esta ambigüidade era
esperada, pois, pela linearidade dos operadores em questão, se
é qualquer número diferente de zero. Esta ambigüidade era
esperada, pois, pela linearidade dos operadores em questão, se
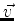 é um autovetor correspondendo a um determinado autovalor,
qualquer múltiplo não-nulo seu também o é. Uma maneira de
levantar a ambigüidade é exigir que o vetor seja normalizado. Isto se
faz assim: o produto escalar de
é um autovetor correspondendo a um determinado autovalor,
qualquer múltiplo não-nulo seu também o é. Uma maneira de
levantar a ambigüidade é exigir que o vetor seja normalizado. Isto se
faz assim: o produto escalar de 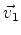 consigo mesmo é
consigo mesmo é
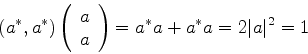 |
(925) |
Logo, devemos ter
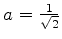 (a fase, como sempre, é
escolhida arbitrariamente). Portanto,
(a fase, como sempre, é
escolhida arbitrariamente). Portanto,
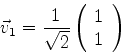 |
(926) |
Um cálculo análogo leva a
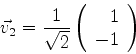 |
(927) |
Note-se que
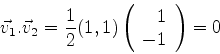 |
(928) |
que mostra que os autovetores são ortogonais, e, portanro, linearmente
independentes. A matriz 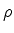 procurada é, então,
procurada é, então,
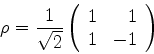 |
(929) |
Como 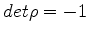 , ela possui inversa, que é
, ela possui inversa, que é
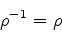 |
(930) |
Resta mostrar que
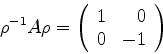 |
(931) |
De fato,
Henrique Fleming 2003
![]() um vetor qualquer de
um vetor qualquer de ![]() , tal que
, tal que
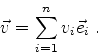
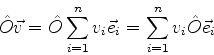

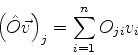
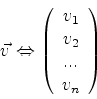

![]() , produto dos operadores
, produto dos operadores ![]() e
e
![]() , é dada pelo produto, no sentido de matrizes, das matrizes que
representam
, é dada pelo produto, no sentido de matrizes, das matrizes que
representam ![]() e
e ![]() , nesta ordem. Recordemos que o produto
das matrizes
, nesta ordem. Recordemos que o produto
das matrizes ![]() , de elementos
, de elementos ![]() e
e ![]() , de elementos
, de elementos ![]() , é a
matriz de elementos
, é a
matriz de elementos
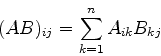
![]() uma segunda base. Podemos escrever
uma segunda base. Podemos escrever

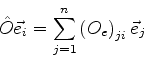
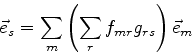
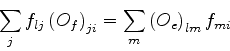
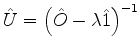 . Então, aplicando-se
. Então, aplicando-se
![]() sendo a incógnita, é uma equação algébrica
de ordem igual à dimensão
sendo a incógnita, é uma equação algébrica
de ordem igual à dimensão ![]() do espaço, ou, o que é o mesmo,
igual à ordem da matriz. Em prinípio tem
do espaço, ou, o que é o mesmo,
igual à ordem da matriz. Em prinípio tem ![]() soluções, mas não
necessariamente distintas. Estas soluções são os autovalores do operador,
e são também chamadas de autovalores da matriz que representa o operador.
A equação (900) é conhecida como equação secular.
soluções, mas não
necessariamente distintas. Estas soluções são os autovalores do operador,
e são também chamadas de autovalores da matriz que representa o operador.
A equação (900) é conhecida como equação secular.
![]() uma matriz, de elementos
uma matriz, de elementos ![]() , que são números
complexos. Seja
, que são números
complexos. Seja ![]() um autovalor da matriz
um autovalor da matriz ![]() . Isto quer dizer que existe
. Isto quer dizer que existe
![]() tal que36
tal que36
![]() ? Sejam
? Sejam