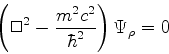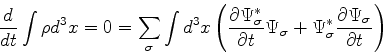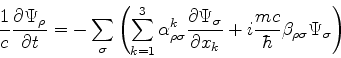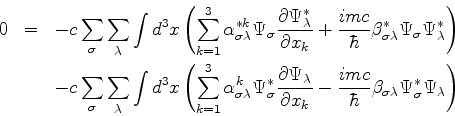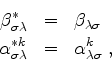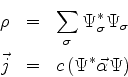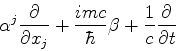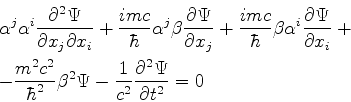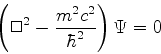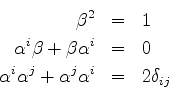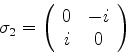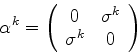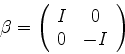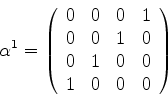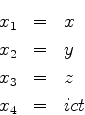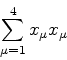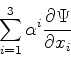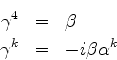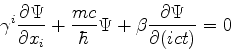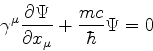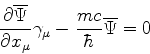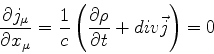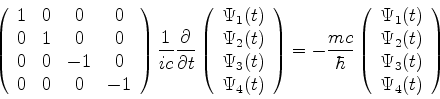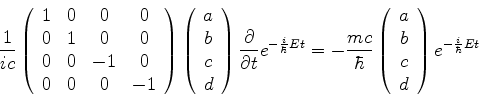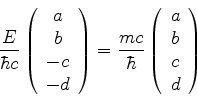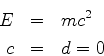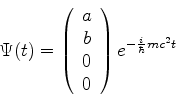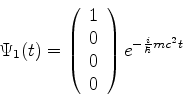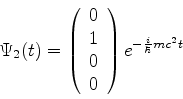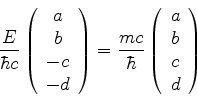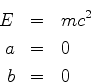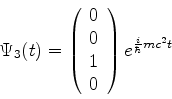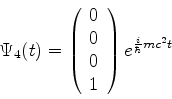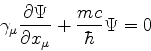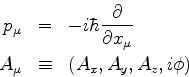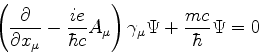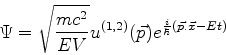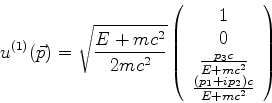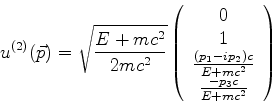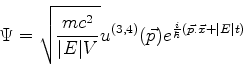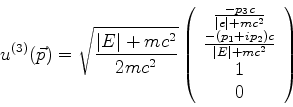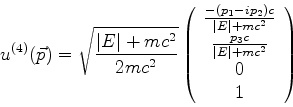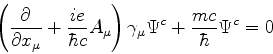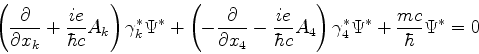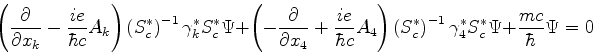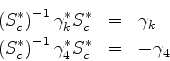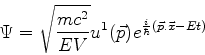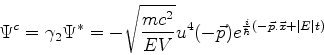Subsections
A Mecânica Quântica Relativista
Estas notas reproduzem parte das transparências apresentadas
no curso de verão de 2003 do Instituto de Física da USP. A parte
relativa à equação de Dirac e à anti-matéria é reproduzida
in toto. Resolvemos substituir a parte que tratava de neutrinos
e do problema solar por indicações à literatura existente, principalmente
na internet, que é de facil acesso e excelente qualidade.
Para o estudo do problema dos neutrinos solares, recomendamos o endereço:
http://www.hep.anl.gov/ndk/hypertext/nuindustry.html
Muitas outras informações sobre o tema, e sobre física em geral, podem
ser encontradas no meu site:
http://hfleming.com
O estudo da equação de Dirac na linha aqui apresentada encontra-se
em
Sakurai, ``Advanced Quantum Mechanics'', Addison-Wesley Press
e em
T. D. Lee, ``Particle Physics and Introduction to Field Theory''.
Um tratamento elementar, mas de qualidade, sobre a física dos
neutrinos encontra-se em
C. Sutton, `` Spaceship Neutrino''
A equação de Schrödinger livre
A equação de Klein-Gordon é de segunda ordem no tempo, o que
cria dificuldades com o postulado básico da Mecânica Quântica
que diz que o estado de um sistema está completamente determinado
(inclusive em sua evolução) se se conhece a função de onda em um instante
qualquer. Além disso, a conservação da probabilidade, expressa pela
equação da continuidade
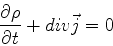 |
(863) |
é satisfeita para
Problemas
1. 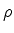 pode ter qualquer sinal.
pode ter qualquer sinal.
2.A equação de Klein-Gordon não é de primeira ordem no tempo.
Procura-se: equação relativista de primeira ordem no tempo. Uma expressão
geral é:
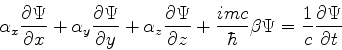 |
(864) |
onde 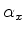 ,
, 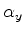 ,
, 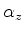 e
e 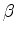 são matrizes quadradas
4x4, e
são matrizes quadradas
4x4, e 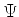 é uma matriz coluna de 4 elementos.
é uma matriz coluna de 4 elementos.
 |
(865) |
Em termos dos elementos de matriz a equação é:
Todos os elementos das 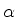 's e de
's e de 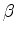 devem ainda ser determinados. Para
isso vamos impôr a condição que, para cada componente
devem ainda ser determinados. Para
isso vamos impôr a condição que, para cada componente 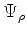 , valha a
equação de Klein-Gordon, ou seja,
, valha a
equação de Klein-Gordon, ou seja,
A motivação é a seguinte. Considere as equações de Maxwell (escritas no sistema
CGS, como todo físico que se preza faz!) na ausência de cargas e correntes:
É um sistema de equações lineares, de primeiro grau, que mistura as várias
componentes de 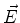 e
e 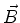 . Tomando o rotacional da última
e usando a penúltima, obtemos
. Tomando o rotacional da última
e usando a penúltima, obtemos
ou
que é a mesma coisa que
para todo 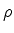 . Obtém-se, de modo análogo, que
. Obtém-se, de modo análogo, que
para todo 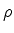 .
.
Ora, a teoria de Maxwell é relativisticamente invariante, e essas duas últimas
relações mostram uma propriedade que essas equações devem satisfazer. Mas elas
não são senão as equações de Klein-Gordon para 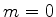 . Logo, justifica-se
a exigência de que, para cada componente de
. Logo, justifica-se
a exigência de que, para cada componente de 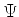 , a equação de Klein-Gordon
seja satisfeita. Resumindo, se
, a equação de Klein-Gordon
seja satisfeita. Resumindo, se 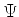 é uma solução da equação de Dirac,
exigiremos que
é uma solução da equação de Dirac,
exigiremos que
para todo 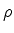 .
.
Preliminarmente precisamos de uma interpretação probabilística.
Gostaríamos de ter
por ser esta uma quantidade positiva e que generaliza o
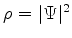 da teoria de Schrödinger. Como
da teoria de Schrödinger. Como
(se a integral é sobre todo o espaço), teremos
Da equação de Dirac se tira
Inserindo esta na penúltima,
de onde segue que
ou seja, 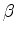 e as
e as 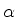 's são hermiteanas.
's são hermiteanas.
Mais precisamente, temos que, com
onde 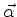 é o ``vetor'' de componentes
é o ``vetor'' de componentes
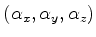 , vale
, vale
Reescrevendo a equação de Dirac como
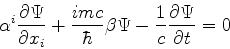 |
(866) |
(onde o primeiro termo representa uma soma sobre 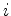 )
e multiplicado à esquerda pelo operador
)
e multiplicado à esquerda pelo operador
temos, após alguns cancelamentos,
Para que isto se reduza a
devemos ter:
Uma solução para essas equações pode ser construída da seguinte maneira:
sejam
As matrizes de Dirac são matrizes 4x4 definidas, em termos das anteriores,
assim:
ou, mais explicitamente,
e assim por diante.
Queremos colocar a equação de Dirac numa forma em que o tempo
e as coordenadas apareçam simetricamente.
Notação:
Assim, o invariante relativístico
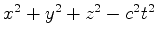 é escrito
é escrito
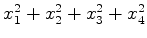 , ou
, ou
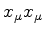 ,
que é a mesma coisa que
,
que é a mesma coisa que
A euqção de Dirac é:
onde
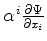 é uma abreviação
para
é uma abreviação
para
Multiplicando a equação de Dirac à esquerda por 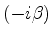 e
introduzindo a notação
e
introduzindo a notação
para 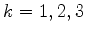 , temos
, temos
ou
com
Seja 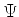 uma solução da equação de Dirac. Definindo
uma solução da equação de Dirac. Definindo
Então obtém-se, da equação de Dirac,
O quadrivetor densidade de corrente de probabilidade,
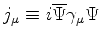 é tal que
é tal que
que é a forma 4-dimensional da equação da continuidade.
Para uma partícula em repouso,
onde 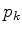 é o operador ``componente
é o operador ``componente 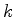 do momento ''. Equivalentemente,
do momento ''. Equivalentemente,
para 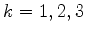 . Logo, para a partícula em repouso,
. Logo, para a partícula em repouso,
Com isso, a equação de Dirac fica:
Explicitamente, temos
Autoestados da energia têm a forma
Logo, para essas funções,
Cancelando as exponenciais reduz-se a
Logo,
ou seja, as soluções são
Todas estas podem ser escritas como combinações lineares
de
e
Soluções de energia negativa
Surpreendentemente, porém, a equação
admite a classe de soluções
como se verifica facilmente. Logo, temos ainda como soluções
as combinações lineares
e
Note que se trata de soluções correspondentes a partículas
livres e em repouso. Além das soluções esperadas, com energia
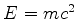 , encontramos outras, totalmente inesperadas,
com energia de repouso dada por
, encontramos outras, totalmente inesperadas,
com energia de repouso dada por 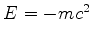 !
Usando, na equação de Dirac
!
Usando, na equação de Dirac
o acoplamento mínimo,
(veja <http://fma.if.usp.br/~fleming/eletromag/index.html>).
Como
obtém-se:
A anti-matéria
A proposta de Dirac para resolver o problema dos estados de
energia negativa é: todos os estados de energia negativa estão
preenchidos, e esta situação é o que chamamos vácuo. Isto faz sentido
porque os elétrons são férmions, e, como se sabe, ``só cabe um
férmion em cada estado''. Vivemos no meio dos estados de energia negativa mas
não os vemos. No entanto, quando um desses elétrons de energia negativa
recebe energia suficiente para pular para um estado de energia positiva
(esta energia é, no mínimo, 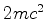 ), deixa, no ``mar de estados de
energia negativa'' um buraco, e este é
observado (como uma partícula de energia positiva e carga positiva,
isto é, oposta à do elétron). Logo, quando um elétron de energia
negativa pula para um estado de energia positiva, aparecem duas coisas:
o próprio elétron, agora ``visível'', e o buraco: chama-se isso de
produção de um par elétron-pósitron. O buraco deixado pelo elétron
é um pósitron, o primeiro exemplo de anti-matéria.
Estas soluções, que são estados de momento e energia definidos
e arbitrários, podem ser obtidas das de repouso por transformações de
Lorentz. Vamos nos limitar a apresentar uma tabela delas. É um exercício
simples verificar que as expressões a seguir efetivamente satisfazem
as equações de Dirac.
), deixa, no ``mar de estados de
energia negativa'' um buraco, e este é
observado (como uma partícula de energia positiva e carga positiva,
isto é, oposta à do elétron). Logo, quando um elétron de energia
negativa pula para um estado de energia positiva, aparecem duas coisas:
o próprio elétron, agora ``visível'', e o buraco: chama-se isso de
produção de um par elétron-pósitron. O buraco deixado pelo elétron
é um pósitron, o primeiro exemplo de anti-matéria.
Estas soluções, que são estados de momento e energia definidos
e arbitrários, podem ser obtidas das de repouso por transformações de
Lorentz. Vamos nos limitar a apresentar uma tabela delas. É um exercício
simples verificar que as expressões a seguir efetivamente satisfazem
as equações de Dirac.
Energia positiva:
Energia negativa:
Dada a equação
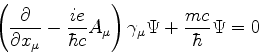 |
(867) |
queremos mostrar que, para cada 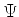 que a resolve, existe
uma
que a resolve, existe
uma 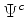 que é solução de:
que é solução de:
com a propriedade
onde 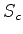 é anti-unitário35. Vamos determinar
é anti-unitário35. Vamos determinar 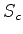 .
Tomando o complexo-conjugado da equação de Dirac, temos
.
Tomando o complexo-conjugado da equação de Dirac, temos
Aplicando 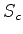 à esquerda, termo a termo, tomando o complexo
conjugado e aplicando, à esquerda,
à esquerda, termo a termo, tomando o complexo
conjugado e aplicando, à esquerda,
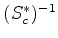 , obtemos
, obtemos
Para que esta equação reproduza Eq.(868), devemos ter
A solução é
com
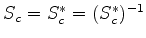 .
Logo,
.
Logo,
Exemplo:
e
Assim, dada uma solução 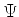 de energia negativa
de energia negativa 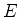 ,
,
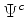 é uma solução de energia
é uma solução de energia 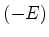 , positiva, de momento
, positiva, de momento
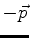 , carga
, carga  e spin no sentido oposto. Trata-se do buraco,
que é um pósitron.
Henrique Fleming 2003
e spin no sentido oposto. Trata-se do buraco,
que é um pósitron.
Henrique Fleming 2003

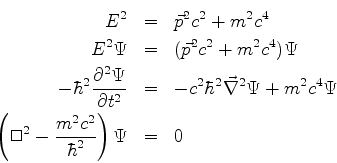
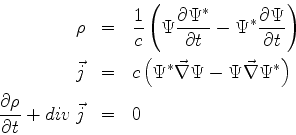
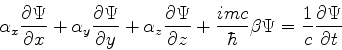

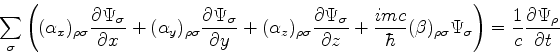
![]() 's e de
's e de ![]() devem ainda ser determinados. Para
isso vamos impôr a condição que, para cada componente
devem ainda ser determinados. Para
isso vamos impôr a condição que, para cada componente ![]() , valha a
equação de Klein-Gordon, ou seja,
, valha a
equação de Klein-Gordon, ou seja,
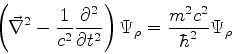
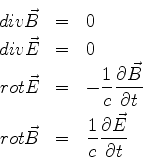
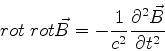
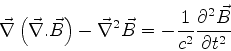
![]() . Logo, justifica-se
a exigência de que, para cada componente de
. Logo, justifica-se
a exigência de que, para cada componente de ![]() , a equação de Klein-Gordon
seja satisfeita. Resumindo, se
, a equação de Klein-Gordon
seja satisfeita. Resumindo, se ![]() é uma solução da equação de Dirac,
exigiremos que
é uma solução da equação de Dirac,
exigiremos que