Sistemas de dois níveis
Embora os sistemas da natureza tenham, em geral, um grande
número de níveis, há situações em que apenas dois deles são
relevantes. Um exemplo importante é este: uma onda
eletromagnética, monocromática, de freqüência
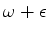 (com
(com
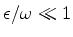 ) incide sobre um átomo (de infinitos
níveis de energia ), que tem, entre eles, dois de energia s tais que
) incide sobre um átomo (de infinitos
níveis de energia ), que tem, entre eles, dois de energia s tais que
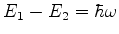 . A freqüência da onda é muito próxima da
diferença de níveis dividida por
. A freqüência da onda é muito próxima da
diferença de níveis dividida por 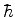 . Mostramos anteriormente
que, neste caso, apenas os níveis
. Mostramos anteriormente
que, neste caso, apenas os níveis 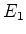 e
e 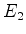 participam do
processo, sendo, os outros, ``espectadores'', que podem, para este
fim específico, ser ignorados.
participam do
processo, sendo, os outros, ``espectadores'', que podem, para este
fim específico, ser ignorados.
Nesta seção vamos estudar sistemas idealizados que têm somente
dois níveis de energia . Supondo que esses níveis não sejam
degenerados, conclui-se que todo conjunto completo e linearmente
independente de vetores de estado deste sistema possui apenas dois
elementos: o conjunto de todos os estados forma, com as operações
usuais de adição e multiplicação por um número complexo, um espaço
vetorial complexo de dimensão 2, e o hamiltoniano, bem como todos
os operadores lineares, podem ser representados por matrizes
complexas 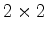 .
.
A equação de Schrödinger é escrita
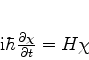 |
(829) |
e, supondo-se que o hamiltoniano não dependa explicitamente do tempo,
pode-se-a integrar formalmente, obtendo
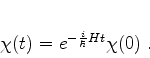 |
(830) |
Por causa da simplicidade do sistema, é possível escrever explicitamente
o operador
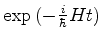 . Os autoestados da
energia ,
. Os autoestados da
energia , 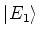 e
e 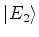 satisfazem as equações
satisfazem as equações
e todo estado 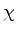 pode ser expandido em termos
deles34:
pode ser expandido em termos
deles34:
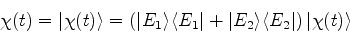 |
(833) |
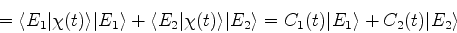 |
(834) |
Uma função 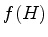 do hamiltoniano é definida assim:
do hamiltoniano é definida assim:
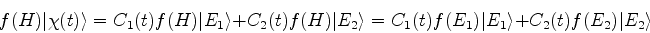 |
(835) |
Usando-se esta operação mostra-se facilmente que
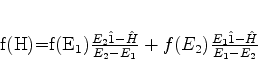 |
(836) |
que, usada para o operador de evolução temporal, dá:
De posse deste resultado, podemos formular a pergunta: suponhamos
que o sistema se encontre, em 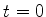 , em um estado
, em um estado
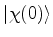 . Qual é a probabilidade de que, decorridos
. Qual é a probabilidade de que, decorridos 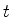 segundos, ele permanecer no mesmo estado?
segundos, ele permanecer no mesmo estado?
Se, em 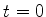 , o estado é
, o estado é 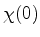 , teremos, no instante
, teremos, no instante 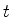 ,
,
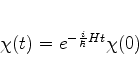 |
(838) |
e, usando a expressão acima,
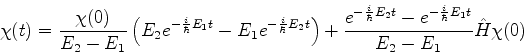 |
(839) |
Seja
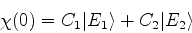 |
(840) |
então,
A probabilidade de o sistema, em 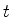 , estar no mesmo estado, é
obtida assim: existe uma base do espaço dos estados formada por
, estar no mesmo estado, é
obtida assim: existe uma base do espaço dos estados formada por
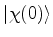 e outros estados, ortogonais a ele. Expandimos
e outros estados, ortogonais a ele. Expandimos
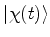 nesta base:
nesta base:
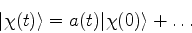 |
(842) |
A probabilidade pedida é 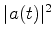 . Ora,
. Ora,
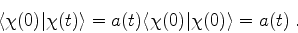 |
(843) |
Logo, a probabilidade é
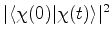 .
Vamos calcular
.
Vamos calcular
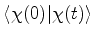 , a amplitude
de probabilidade. Usando (839), temos
, a amplitude
de probabilidade. Usando (839), temos
Como
Então,
Suponhamos que 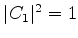 e
e 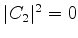 . Então, após uma
álgebra simples,
. Então, após uma
álgebra simples,
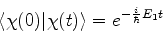 |
(846) |
logo,
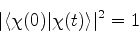 |
(847) |
isto é, um sistema que está num estado estacionário permanece nele
(daí se chamar estacionário!).
É fácil mostrar que os estados estacionários são os únicos que
possuem esta propriedade. De fato, se
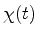 |
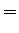 |
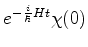 |
(848) |
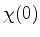 |
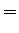 |
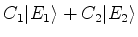 |
(849) |
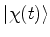 |
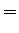 |
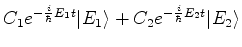 |
(850) |
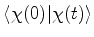 |
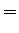 |
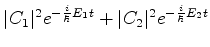 |
(851) |
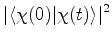 |
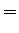 |
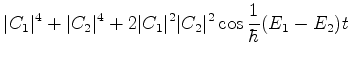 |
(852) |
Para que
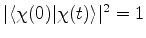 para todo
para todo 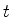 , temos de ter
ou
, temos de ter
ou 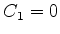 ou
ou 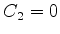 . Em qualquer dos casos o outro coeficiente é
de módulo 1, pois
. Em qualquer dos casos o outro coeficiente é
de módulo 1, pois
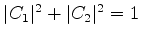 . Logo,
. Logo,
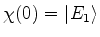 ou
ou
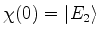 .
.
Tomemos agora uma base arbitrária do espaço dos estados, formada por
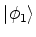 e
e
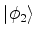 . O estado
. O estado
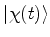 é
expandido, nesta base, como
é
expandido, nesta base, como
 |
(853) |
Introduzindo a notação
temos
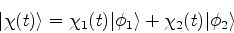 |
(854) |
A equação de Schrödinger é
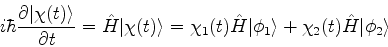 |
(855) |
e, tomando os produtos escalares com
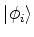 ,
,
Denotando
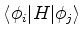 por
por 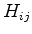 , temos
, temos
Para estados estacionários,
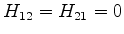 . Logo, os elementos de
matriz
. Logo, os elementos de
matriz 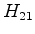 e
e 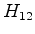 promovem as transições entre estados.
promovem as transições entre estados.
De fato, seja
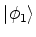 um dos estados da base.
um dos estados da base.
Qual é a probabilidade de que, em algum 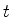 , o sistema se encontre em
, o sistema se encontre em
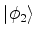 ?
A amplitude é dada por
?
A amplitude é dada por
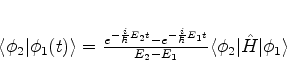 |
(862) |
Não há transição se 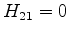 .
.
As equações (863) são as Eqs.(8.43) do Volume III das ``Feynman
Lectures on Physics'', que as utiliza para um grande número de aplicações
interessantes. Vamos fazer o mesmo.
Henrique Fleming 2003
![]() .
.
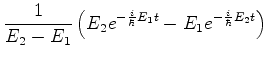
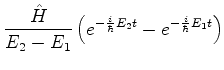
![]() , o estado é
, o estado é ![]() , teremos, no instante
, teremos, no instante ![]() ,
,
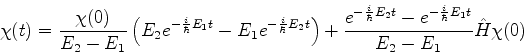
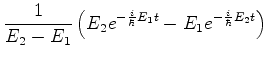
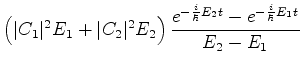
![]() e
e
![]() . O estado
. O estado
![]() é
expandido, nesta base, como
é
expandido, nesta base, como
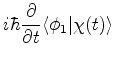
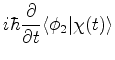
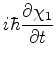
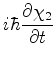
![]() um dos estados da base.
um dos estados da base.