A energia potencial 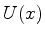 consiste de dois poços de potencial
simétricos, separados por uma barreira. Na figura abaixo os
poços são as regiões I e II, e a barreira tem altura
consiste de dois poços de potencial
simétricos, separados por uma barreira. Na figura abaixo os
poços são as regiões I e II, e a barreira tem altura 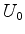 .
Se a barreira fosse impenetrável, haveria níveis de energia
relativos ao movimento da partícula em um ou outro dos dois
poços, ou seja, duas famílias de níveis iguais, uma em
cada poço. O fato de que o tunelamento através da barreira
existe na mecânica quântica faz com que cada um dos níveis
relativos ao movimento em um dos poços se separe em dois
níveis próximos, correspondendo agora a estados da
partícula em que ela está nos dois poços.
.
Se a barreira fosse impenetrável, haveria níveis de energia
relativos ao movimento da partícula em um ou outro dos dois
poços, ou seja, duas famílias de níveis iguais, uma em
cada poço. O fato de que o tunelamento através da barreira
existe na mecânica quântica faz com que cada um dos níveis
relativos ao movimento em um dos poços se separe em dois
níveis próximos, correspondendo agora a estados da
partícula em que ela está nos dois poços.
A determinação deste desdobramento de níveis
é simples no caso em que se pode usar a aproximação quase
clássica. É o que faremos agora.
Uma solução aproximada da equação de Schrödinger para a energia potencial
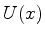 , desprezando a probabilidade de passagem pela barreira, pode ser construída
com a função quase-clássica
, desprezando a probabilidade de passagem pela barreira, pode ser construída
com a função quase-clássica 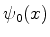 , que descreve o movimento com uma
certa energia
, que descreve o movimento com uma
certa energia 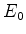 em um dos poços (digamos, o poço I), e que é exponencialmente decrescente
em ambos os lados do poço I. A normalização aproximada desta função é
em um dos poços (digamos, o poço I), e que é exponencialmente decrescente
em ambos os lados do poço I. A normalização aproximada desta função é
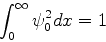 |
(804) |
Portanto, para 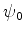 , temos satisfeita a equação de Schrödinger
, temos satisfeita a equação de Schrödinger
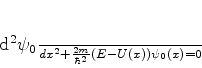 |
(805) |
no seguinte sentido: para 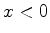 a equação é aproximadamente satisfeita porque,
tanto
a equação é aproximadamente satisfeita porque,
tanto 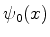 quanto sua derivada segunda, nesta região, são aproximadamente
nulas.
quanto sua derivada segunda, nesta região, são aproximadamente
nulas.
O produto
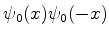 , para
, para 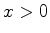 , é
desprezível.
O potencial como um todo é simétrico. A
equação de Schrödinger
, é
desprezível.
O potencial como um todo é simétrico. A
equação de Schrödinger
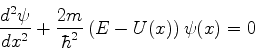 |
(806) |
permanece válida quando se troca 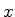 por
por 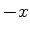 . Logo, se
. Logo, se 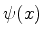 é uma função de onda,
é uma função de onda, 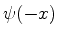 também o é, para o mesmo
valor de
também o é, para o mesmo
valor de 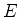 . Como não há degenerescência, temos
. Como não há degenerescência, temos
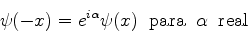 |
(807) |
Logo,
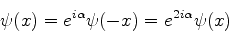 |
(808) |
e portanto
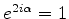 , de onde segue que
, de onde segue que 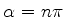 . Temos,
em conseqüência,
. Temos,
em conseqüência,
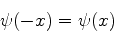 |
(809) |
ou
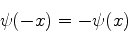 |
(810) |
As autofunções da energia deste sistema são, portanto,
funções pares ou ímpares de 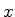 . Isto é uma
conseqüência de que
. Isto é uma
conseqüência de que 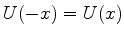 .
As funções de onda corretas, na aproximação quase-clássica, são obtidas
construíndo, a partir de
.
As funções de onda corretas, na aproximação quase-clássica, são obtidas
construíndo, a partir de 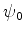 , as funções
, as funções 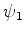 , simétrica,
e
, simétrica,
e 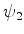 , anti-simétrica:
, anti-simétrica:
Note que a função 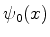 não é autofunção do
hamiltoniano com a energia potencial
não é autofunção do
hamiltoniano com a energia potencial 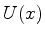 , simétrica: é a
função de onda que teríamos de a barreira fosse
impenetrável. Tanto que
, simétrica: é a
função de onda que teríamos de a barreira fosse
impenetrável. Tanto que  é desprezível,
enquanto que
é desprezível,
enquanto que 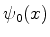 não o é.
De novo, como os níveis não são degenerados, devemos ter energia s diferentes
para
não o é.
De novo, como os níveis não são degenerados, devemos ter energia s diferentes
para 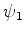 e
e 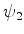 .
Sejam
.
Sejam
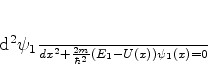 |
(813) |
a equação de Schrödinger para 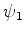 , e
, e
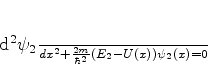 |
(814) |
aquela para 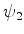 .
Multiplicando (806) por
.
Multiplicando (806) por 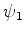 e (814) por
e (814) por 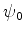 e subtraíndo, temos
e subtraíndo, temos
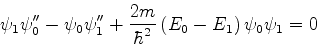 |
(815) |
ou
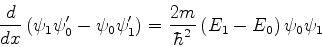 |
(816) |
Integrando de 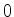 a
a 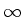 :
:
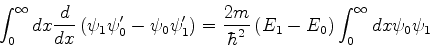 |
(817) |
onde usamos o fato de
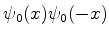 ser muito pequeno.
Lembrando que as funções que aparecem no primeiro membro se anulam no
infinito, temos
ser muito pequeno.
Lembrando que as funções que aparecem no primeiro membro se anulam no
infinito, temos
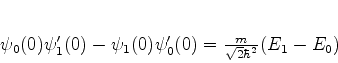 |
(819) |
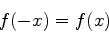 |
(820) |
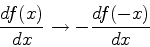 |
(821) |
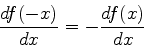 |
(822) |
Voltando à (820),
![\begin{displaymath}
\psi_{1}(0)=\frac{1}[\sqrt{2}\left[\psi_{0}(0)+\psi_{0}(0)\right]=\sqrt{2}\psi_{0}(0)
\end{displaymath}](img2296.png) |
(823) |
enquanto
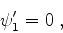 |
(824) |
levando a
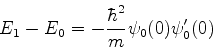 |
(825) |
Repetindo agora o cálculo com 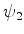 e
e 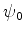 , obtemos,
ao longo dos mesmos passos,
, obtemos,
ao longo dos mesmos passos,
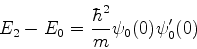 |
(826) |
Subtraíndo, obtemos
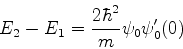 |
(827) |
Um cálculo mais refinado leva ao resultado
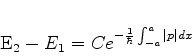 |
(828) |
onde 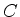 é uma constante, e
é uma constante, e 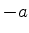 e
e 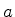 são indicados na figura. A
eq.(829) torna explícito o papel do tunelamento
na separação dos níveis de energia .
são indicados na figura. A
eq.(829) torna explícito o papel do tunelamento
na separação dos níveis de energia .
Henrique Fleming 2003
{$E_{2}$}
\uput[0](8,4){$I$}\uput[0](4,4){$II$}
\end{pspicture}](img2260.png)
![$\displaystyle \frac{1}{\sqrt{2}}\left[\psi_{0}(x)+\psi_{0}(-x)\right]$](img2277.png)
![$\displaystyle \frac{1}{\sqrt{2}}\left[\psi_{0}(x)-\psi_{0}(-x)\right]$](img2279.png)
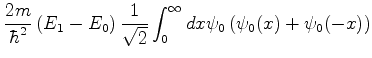
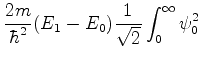
![\begin{displaymath}
\psi_{1}(0)=\frac{1}[\sqrt{2}\left[\psi_{0}(0)+\psi_{0}(0)\right]=\sqrt{2}\psi_{0}(0)
\end{displaymath}](img2296.png)