Subsections
O caso quase-clássico
Iniciamos o nosso curso com o estudo do átomo de Bohr, centrado na
regra de quantização, para órbitas circulares,
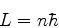 |
(754) |
com 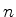 inteiro, que dá, para a energia ,
inteiro, que dá, para a energia ,
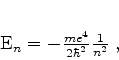 |
(755) |
a famosa fórmula de Bohr.
Na verdade, (756) é o caso particular, para órbitas
circulares, das regras de Bohr-Sommerfeld, que podem ser
enunciadas assim: seja um sistema periódico descrito por
coordenadas generalizadas 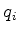 ,
, 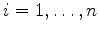 . Então
. Então
 |
(756) |
onde 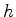 é a constante de Planck, e os
é a constante de Planck, e os 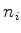 são inteiros. No
caso do átomo de hidrogênio, o movimento, em órbita circular, pode
ser inteiramente descrito pela coordenada angular
são inteiros. No
caso do átomo de hidrogênio, o movimento, em órbita circular, pode
ser inteiramente descrito pela coordenada angular 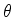 , do par
, do par
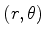 de coordenadas polares no plano da órbita. Como a
lagrangeana do sistema é
de coordenadas polares no plano da órbita. Como a
lagrangeana do sistema é
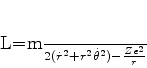 |
(757) |
temos que
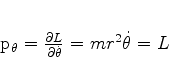 |
(758) |
onde 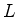 é o momento angular. Além disso,
é o momento angular. Além disso, 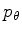 é
constante, pois a variável
é
constante, pois a variável 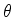 não aparece na lagrangeana.
Então,
não aparece na lagrangeana.
Então,
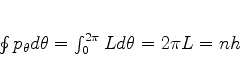 |
(759) |
ou seja,
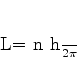 |
(760) |
que é a regra de Bohr usual.
Estamos agora muito distantes dessa versão simples de
uma mecânica quântica. Órbitas não existem, de modo que a regra de
Bohr nem pode ser enunciada, com o vocabulário da mecânica
quântica. No entanto,(756) permanece válida, embora
obtida de maneira totalmente diferente.
Nesta seção queremos investigar se existem condições em que a
regra de Bohr seja aproximadamente válida. Sistemas que satisfazem
a essas condições serão chamados quase-clássicos33. No estilo
que temos adotado sistematicamente, estudaremos este problema no
contexto dos estados estacionários e, para simplificar, para
sistemas unidimensionais.
Uma partícula de massa 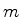 possui uma energia potencial
possui uma energia potencial 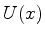 . A
equação de Schrödinger para estados estacionários é:
. A
equação de Schrödinger para estados estacionários é:
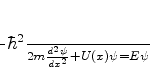 |
(761) |
que, naturalmente, pode ser escrita como
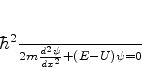 |
(762) |
Procuraremos soluções escritas na forma
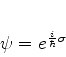 |
(763) |
onde 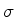 é uma função complexa, e tal que
é uma função complexa, e tal que
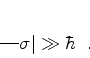 |
(764) |
Note-se que, sendo 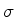 complexa, temos
complexa, temos
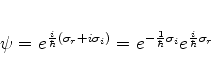 |
(765) |
ou seja, (764) é uma expressão geral para a função de
onda. É a condição (765) que nos dirige ao caso que nos
interessa, já que é uma realização do limite formal
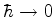 , supostamente a situação em que a mecânica quântica
tende à mecânica clássica (as relações de incerteza inexistem,
nesse limite).
, supostamente a situação em que a mecânica quântica
tende à mecânica clássica (as relações de incerteza inexistem,
nesse limite).
Inserindo na eq.(763) a expressão (764),
obtemos a seguinte equação para 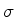 (completamente
equivalente à equação de Schrödinger):
(completamente
equivalente à equação de Schrödinger):
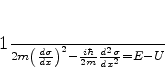 |
(766) |
Vamos agora utilizar a condição (765). Suponhamos que
exista a expansão
 |
(767) |
com 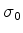 ,
, 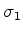 ,
, 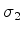 finitos (ou seja,de
módulos muito maiores do que
finitos (ou seja,de
módulos muito maiores do que 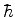 ). Então (765)
estará garantida desde que
). Então (765)
estará garantida desde que
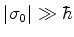 .
.
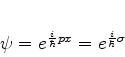 |
(768) |
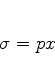 |
(769) |
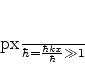 |
(770) |
Utilizando (768) em (767), obtemos
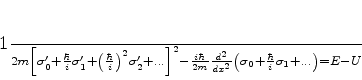 |
(771) |
onde a derivação em relação a 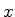 é denotada por um
é denotada por um 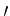 .
Igualando os coeficientes da potência 0 de
.
Igualando os coeficientes da potência 0 de 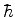 , temos
, temos
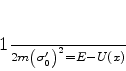 |
(772) |
que dá
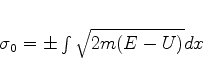 |
(773) |
A relação
permite escrever
de maneira que (774) pode ser
escrita
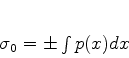 |
(774) |
Voltando à (772), igualemos os coeficientes da
potência  de
de 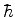 :
:
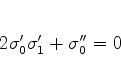 |
(775) |
Como, de (775),
temos
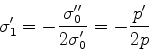 |
(776) |
ou
 |
(777) |
Temos, portanto, até esta aproximação,
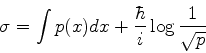 |
(778) |
ou
 |
(779) |
Mais precisamente, a solução geral é dada por uma combinação
linear das soluções exibidas acima, ou seja,
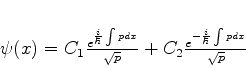 |
(780) |
As condições de validade da aproximação quase-clássica são obtidas
insistindo-se em que, na equação (767), o segundo termo do
primeiro membro seja muito menor que o primeiro isto é:
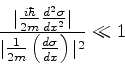 |
(781) |
Isto é equivalente a
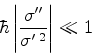 |
(782) |
ou ainda,
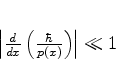 |
(783) |
Aqui encontramos mais uma vez uma situação importante em que a
aproximação quase-clássica não é válida: quando o momento se
anula, a eq.(784) não é satisfeita.
Suponhamos que a nossa partícula possua uma energia potencial
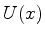 , e que sua energia total seja
, e que sua energia total seja 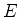 . Como temos
. Como temos
vemos que, nos pontos em que 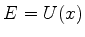 ,
, 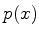 é igual à zero,
e a aproximação quase-clássica falha.
é igual à zero,
e a aproximação quase-clássica falha.
Na figura acima vemos os pontos 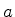 e
e 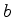 , em que
, em que 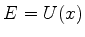 , e a
aproximação quase-clássica falha. Classicamente são os pontos em
que a partícula pára e volta, os ``pontos de retorno'''. Nas
vizinhanças desses pontos não podemos utilizar a expressão
(781). Há uma série de métodos para contornar esta
dificuldade. O mais elementar é o seguinte: seja
, e a
aproximação quase-clássica falha. Classicamente são os pontos em
que a partícula pára e volta, os ``pontos de retorno'''. Nas
vizinhanças desses pontos não podemos utilizar a expressão
(781). Há uma série de métodos para contornar esta
dificuldade. O mais elementar é o seguinte: seja 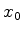 um ponto
de retorno, ou seja,
um ponto
de retorno, ou seja, 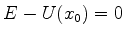 . A equação de Schrödinger é
. A equação de Schrödinger é
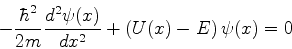 |
(784) |
Expandindo a função
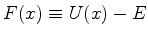 em torno do ponto
em torno do ponto 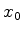 , temos
, temos
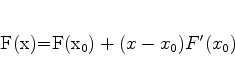 |
(785) |
com 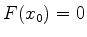 . Como
. Como 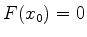 , temos
, temos
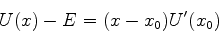 |
(786) |
Logo, nas vizinhanças do ponto de retorno, a equação de Schrödinger é
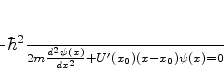 |
(787) |
que é a equação de Schrödinger para uma partícula sobre a ação de uma
força constante. Mas esta equação pode ser resolvida exatamente (veja Apêndice),
de maneira que podemos proceder assim: a uma certa (pequena) distância do
ponto de retorno, usamos a função de onda quase-clássica. Mais para perto do
ponto de retorno, usamos a solução exata (788). Tudo o que precisamos
fazer é achar, dentre as soluções de (788),aquela que se acopla
continuamente com a solução semi-clássica.
Este método utiliza funções transcendentes (a função de Airy, por
exemplo), e um pouco de análise complexa, o que está acima do
nível deste curso. Assim, sendo, limitar-nos-emos a enviar o
leitor ao apêndice, para os detalhes do cálculo, e a dar a regra
de transição, lá obtida.
Nas regiões classicamente inacessíveis, temos  , logo,
, logo,
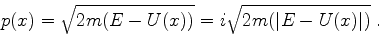 |
(788) |
Uma repetição simples dos cálculos leva a
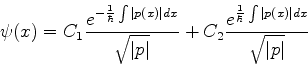 |
(789) |
Temos,portanto,
Vamos nos limitar a enunciar a regra de transição,
ilustrando-a com exemplos.
Seja 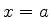 um ponto de retorno, ou seja, tal que
um ponto de retorno, ou seja, tal que  . Então,
. Então,
A figura acima mostra um poço de potencial e os pontos, 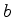 e
e 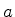 ,
de retorno de uma partícula de massa
,
de retorno de uma partícula de massa 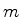 e energia
e energia 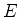 .
.
Considere o ponto de retorno 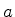 . À sua direita a função de onda
deve decrescer exponencialmente, já que se trata de uma região
classicamente proibida, com
. À sua direita a função de onda
deve decrescer exponencialmente, já que se trata de uma região
classicamente proibida, com 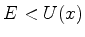 . Dentre as soluções de
(794), a que nos serve é escrita
. Dentre as soluções de
(794), a que nos serve é escrita
logo, à esquerda de 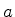 , teremos
, teremos
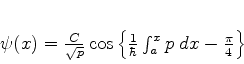 |
(793) |
Passemos ao ponto de retorno 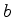 . À sua esquerda temos uma região
classicamente proibida. Devemos, então, ter uma função de onda
que, à medida que nos aprofundamos nessa região (isto é, à medida
que
. À sua esquerda temos uma região
classicamente proibida. Devemos, então, ter uma função de onda
que, à medida que nos aprofundamos nessa região (isto é, à medida
que 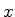 se torna mais e mais negativo), decresce exponencialmente.
Dentre as catalogadas em (794) a que tem essas
propriedades é
se torna mais e mais negativo), decresce exponencialmente.
Dentre as catalogadas em (794) a que tem essas
propriedades é
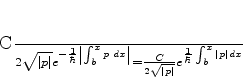 |
(794) |
logo, a função de onda à direita de 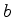 será
será
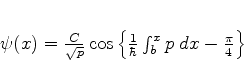 |
(795) |
Conseqüentemente temos, na região
 , as expressões
(794) e (796) para a função de onda.
Essas duas expressões devem então coincidir:
, as expressões
(794) e (796) para a função de onda.
Essas duas expressões devem então coincidir:
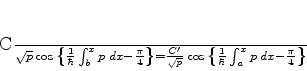 |
(796) |
Tomando 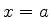 , obtemos
, obtemos
 |
(797) |
que leva a
A regra de Bohr-Sommerfeld contém uma integral num circuito
fechado. Neste caso, isto seria
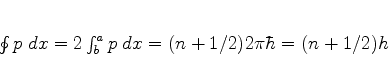 |
(799) |
Obtemos uma relação que coincide com a regra de Bohr para grandes
valores de 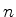 , quando se pode desprezar o termo
, quando se pode desprezar o termo 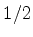 .
Neste caso a energia potencial é
.
Neste caso a energia potencial é
e
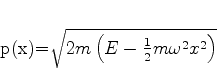 |
(800) |
Os pontos de retorno acontecem quando a energia coincide com a
energia potencial, isto é
o que acontece para
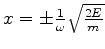 . A
integral que aparece em (799) é
. A
integral que aparece em (799) é
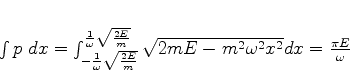 |
(801) |
e temos, então,
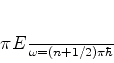 |
(802) |
ou
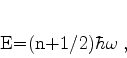 |
(803) |
em completa coincidência com o resultado exato!
Henrique Fleming 2003
![]() ,
, ![]() . Então
. Então
![]() possui uma energia potencial
possui uma energia potencial ![]() . A
equação de Schrödinger para estados estacionários é:
. A
equação de Schrödinger para estados estacionários é:
![]() (completamente
equivalente à equação de Schrödinger):
(completamente
equivalente à equação de Schrödinger):
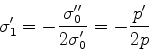

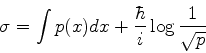

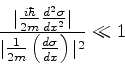
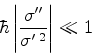
![]() , e que sua energia total seja
, e que sua energia total seja ![]() . Como temos
. Como temos
{$E$}
\uput[0](-0.2,7.5){$U(x)$}
\uput[0](11.5,3.6){$x$}
\end{pspicture}](img2218.png)
![]() , logo,
, logo,
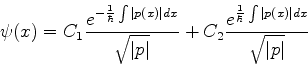
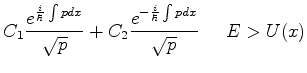
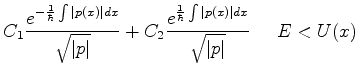
![]() um ponto de retorno, ou seja, tal que
um ponto de retorno, ou seja, tal que ![]() . Então,
. Então,
{$E$}
\uput[0](-0.2,7.5){$U(x)$}
\uput[0](11.5,3.6){$x$}
\end{pspicture}](img2218.png)
![]() . À sua direita a função de onda
deve decrescer exponencialmente, já que se trata de uma região
classicamente proibida, com
. À sua direita a função de onda
deve decrescer exponencialmente, já que se trata de uma região
classicamente proibida, com ![]() . Dentre as soluções de
(794), a que nos serve é escrita
. Dentre as soluções de
(794), a que nos serve é escrita
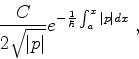
![]() . À sua esquerda temos uma região
classicamente proibida. Devemos, então, ter uma função de onda
que, à medida que nos aprofundamos nessa região (isto é, à medida
que
. À sua esquerda temos uma região
classicamente proibida. Devemos, então, ter uma função de onda
que, à medida que nos aprofundamos nessa região (isto é, à medida
que ![]() se torna mais e mais negativo), decresce exponencialmente.
Dentre as catalogadas em (794) a que tem essas
propriedades é
se torna mais e mais negativo), decresce exponencialmente.
Dentre as catalogadas em (794) a que tem essas
propriedades é
![]() , obtemos
, obtemos