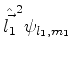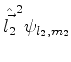Subsections
Partículas idênticas
Na mecânica quântica se diz que duas partículas são
idênticas se a operação de trocar uma pela outra não tem qualquer
efeito físico no sistema ao qual pertencem: não há maneira de
realizar uma medida física que detete se tal mudança foi realizada.
Para explorar as conseqüências disso de maneira formal,
introduzimos o operador 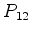 de troca de partículas. Seja
de troca de partículas. Seja
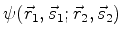 uma função de onda do sistema
onde incluímos as variáveis de spin,
uma função de onda do sistema
onde incluímos as variáveis de spin, 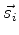 . O operador de
troca atua assim:
. O operador de
troca atua assim:
 |
(734) |
Se as partículas são verdadeiramente idênticas, o hamiltoniano
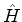 deve ser simétrico em relação às variáveis de posição
e spin das partículas idênticas, de maneira que não haja
qualquer mudança na energia do sistema quando a troca ocorre.
deve ser simétrico em relação às variáveis de posição
e spin das partículas idênticas, de maneira que não haja
qualquer mudança na energia do sistema quando a troca ocorre.
Neste caso,
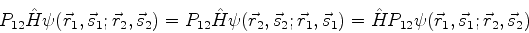 |
(735) |
ou seja,
![\begin{displaymath}[P_{12}, \hat{H}]=0
\end{displaymath}](img2113.png) |
(736) |
para todo hamiltoniano simétrico pela troca de partículas
idênticas.
Seja 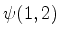 uma autofunção do operador
uma autofunção do operador 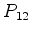 :
:
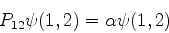 |
(737) |
Temos
logo,
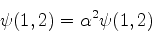 |
(740) |
de onde se tira que
 . Logo, as autofunções do operador
. Logo, as autofunções do operador
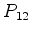 são tais que
são tais que
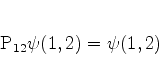 |
(741) |
ou
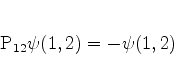 |
(742) |
isto é, são as funções pares e ímpares pela troca de um par de
partículas idênticas. Como
![$[P_{12}, \hat{H}]=0$](img2124.png) , o operador
, o operador
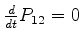 , e o valor médio de
, e o valor médio de 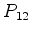 é constante,
o que se estende para os autovalores . Portanto, o autovalor de
é constante,
o que se estende para os autovalores . Portanto, o autovalor de
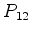 é uma constante do movimento.
é uma constante do movimento.
Partículas para as quais a eq.(742) são ditas
bosons , e satisfazem a estaística de Bose-Einstein; partículas
para as quais a eq.(743) é satisfeita são ditas
férmions, e satisfazem a estatística de Fermi-Dirac.
Empiricamente se verifica que os bosons são partículas de spin
inteiro, enquanto que os férmions são partículas de spin
1/2, 3/2, etc. Os elétrons são férmions, os fótons são
bosons .
O princípio de Pauli
O tipo de estatística satisfeita por uma partícula tem
conseqüências bem definidas sobre seu movimento. Examinemos
a função de onda de dois férmions idênticos, e imaginemos que
eles ocupassem ambos a mesma posição, tendo o mesmo valor
para a componente 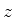 do spin. Ou seja,
do spin. Ou seja,
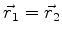 e
e
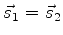 . Então, se a função de onda do sistema
for
. Então, se a função de onda do sistema
for
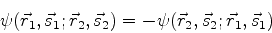 |
(743) |
Nas condições acima, teríamos
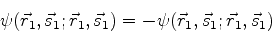 |
(744) |
ou
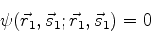 |
(745) |
mostrando que a probabilidade de dois férmions ocuparem o mesmo
estado (o estado, aqui, é completamente definido pela posição e pela
componente 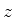 do spin) é zero. Isto é denominado princípio de
exclusão, ou princípio de Pauli. Um exemplo importante é o seguinte:
considere dois elétrons movendo-se em um campo de forças, como, por
exemplo, no átomo de Hélio. Desprezando a interação entre os elétrons,
e denotando por
do spin) é zero. Isto é denominado princípio de
exclusão, ou princípio de Pauli. Um exemplo importante é o seguinte:
considere dois elétrons movendo-se em um campo de forças, como, por
exemplo, no átomo de Hélio. Desprezando a interação entre os elétrons,
e denotando por 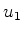 e
e 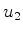 dois estados estacionários de 1 elétron
nesse campo, a função de onda de um estado estacionário admissível
seria
dois estados estacionários de 1 elétron
nesse campo, a função de onda de um estado estacionário admissível
seria
![\begin{displaymath}
\psi = \frac{1}{\sqrt{2}}\left[u_{1}(\vec{r}_{1},\vec{s}_{...
...\vec{r}_{2},\vec{s}_{2})u_{2}(\vec{r}_{1},\vec{s}_{1})\right]
\end{displaymath}](img2133.png) |
(746) |
A função de onda (747) satisfaz a propriedade
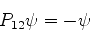 |
(747) |
e se anula identicamente se 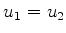 . Em contraposição, o ``estado'' de
função de onda
. Em contraposição, o ``estado'' de
função de onda
![\begin{displaymath}
\psi^{\prime} = \frac{1}{\sqrt{2}}\left[u_{1}(\vec{r}_{1},...
...\vec{r}_{2},\vec{s}_{2})u_{2}(\vec{r}_{1},\vec{s}_{1})\right]
\end{displaymath}](img2136.png) |
(748) |
que tem a propriedade
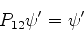 |
(749) |
não existe na natureza, assim como nenhum outro que não esteja antissimetrizado.
A expressão costumeira desta lei é que duas partículas idênticas de spin
semi-inteiro não podem estar em um estado em que se movem na mesma ``órbita'' e
com os spins paralelos. Dois elétrons podem estar na mesma ``órbita'', desde que seus
spins sejam anti-paralelos32.
No átomo de Hélio, se ignorarmos a interação entre os elétrons, tudo se passa como se
cada elétron estivesse sob a ação de uma campo coulombiano, e as funções de onda individuais
de cada elétron seriam as de um elétron do átomo de Hidrogênio (com a diferença
que 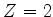 ). Então, nessa aproximação, no estado fundamental, poderia haver dois elétrons
no estado
). Então, nessa aproximação, no estado fundamental, poderia haver dois elétrons
no estado 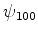 , um com ``spin para cima'', o outro com ``spin para baixo''. O elemento
de
, um com ``spin para cima'', o outro com ``spin para baixo''. O elemento
de 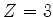 é o Lítio. Na mesma aproximação (de desprezar a interação entre os elétrons),
não seria possível adicionar mais um elétron no estado
é o Lítio. Na mesma aproximação (de desprezar a interação entre os elétrons),
não seria possível adicionar mais um elétron no estado 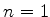 . Este teria de ser
acomodado em um estado com
. Este teria de ser
acomodado em um estado com 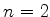 . É claro que desprezar a interação entre os elétrons
é tanto mais grave quanto mais numerosos eles são, de modo que vamos parar por aqui.
. É claro que desprezar a interação entre os elétrons
é tanto mais grave quanto mais numerosos eles são, de modo que vamos parar por aqui.
Adição de momento s angulares
O problema é este: dadas duas partículas em estados de momento angular bem definido,
qual o valor, ou valores, do momento angular do sistema composto pelas duas? Como a solução
é consideravelmente técnica, vamos nos limitar aqui a dar os resultados.
Seja
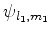 o estado de uma das partículas, e
o estado de uma das partículas, e
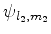 o estado
da outra. Isto quer dizer que, se
o estado
da outra. Isto quer dizer que, se
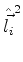 e
e
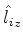 (
(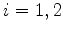 ) forem
os operadores de momento angular total e componente
) forem
os operadores de momento angular total e componente 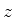 do momento angular, teremos
do momento angular, teremos
Considerando agora o sistema composto, teremos que o momento angular total pode ter
todos os valores entre 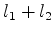 e
e 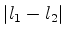 , variando de um em um. Para a componente
, variando de um em um. Para a componente
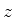 do momento angular total, a regra é mais simples: a componente
do momento angular total, a regra é mais simples: a componente 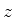 do momento angular
total é a soma algébrica das componentes
do momento angular
total é a soma algébrica das componentes 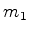 e
e 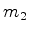 .
.
Para um tratamento completo desta questão, veja [3].
Henrique Fleming 2003
![]() uma autofunção do operador
uma autofunção do operador ![]() :
:
![]() ). Então, nessa aproximação, no estado fundamental, poderia haver dois elétrons
no estado
). Então, nessa aproximação, no estado fundamental, poderia haver dois elétrons
no estado ![]() , um com ``spin para cima'', o outro com ``spin para baixo''. O elemento
de
, um com ``spin para cima'', o outro com ``spin para baixo''. O elemento
de ![]() é o Lítio. Na mesma aproximação (de desprezar a interação entre os elétrons),
não seria possível adicionar mais um elétron no estado
é o Lítio. Na mesma aproximação (de desprezar a interação entre os elétrons),
não seria possível adicionar mais um elétron no estado ![]() . Este teria de ser
acomodado em um estado com
. Este teria de ser
acomodado em um estado com ![]() . É claro que desprezar a interação entre os elétrons
é tanto mais grave quanto mais numerosos eles são, de modo que vamos parar por aqui.
. É claro que desprezar a interação entre os elétrons
é tanto mais grave quanto mais numerosos eles são, de modo que vamos parar por aqui.
![]() o estado de uma das partículas, e
o estado de uma das partículas, e
![]() o estado
da outra. Isto quer dizer que, se
o estado
da outra. Isto quer dizer que, se
![]() e
e
![]() (
(![]() ) forem
os operadores de momento angular total e componente
) forem
os operadores de momento angular total e componente ![]() do momento angular, teremos
do momento angular, teremos