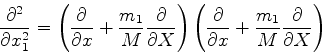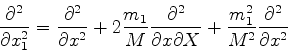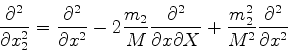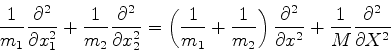Subsections
Qual é a probabilidade de, lançando-se um dado, obter-se
o número 3? Todo o mundo sabe que é 1/6. Qual é a probabilidade
de, lançando-se o mesmo dado duas vezes, obter-se duas vezes o
número 3? Como são eventos independentes, a probabilidade é o
produto, 1/36, portanto. Considere agora o seguinte problema:
lança-se o dado uma primeira vez, obtendo-se 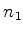 . Qual é
a probabilidade de que, num segundo arremesso, a leitura,
. Qual é
a probabilidade de que, num segundo arremesso, a leitura, 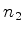 ,
seja maior do que
,
seja maior do que 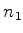 ? Ou seja, qual é a probabilidade de,
arremessando-se um dado duas vezes, obter-se o par (
? Ou seja, qual é a probabilidade de,
arremessando-se um dado duas vezes, obter-se o par (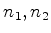 ),
com
),
com  ? Agora não se trata de eventos
independentes, e a probabilidade não é um simples produto.
Num sistema formado por duas partículas, dizemos que elas são
independentes se a probabilidade de uma estar em uma certo elemento
de volume for independente da posição da outra. Neste caso, cada
partícula possui a sua própria função de onda. Sejam
? Agora não se trata de eventos
independentes, e a probabilidade não é um simples produto.
Num sistema formado por duas partículas, dizemos que elas são
independentes se a probabilidade de uma estar em uma certo elemento
de volume for independente da posição da outra. Neste caso, cada
partícula possui a sua própria função de onda. Sejam
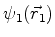 e
e
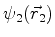 essas funções de
onda. Então a função de onda do sistema é, simplesmente,
essas funções de
onda. Então a função de onda do sistema é, simplesmente,
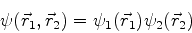 |
(703) |
De fato, desta forma a probabilidade de a partícula  estar entre
estar entre
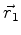 e
e
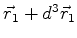 e da partícula
e da partícula 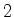 estar
entre
estar
entre 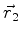 e
e
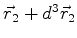 é dada por
é dada por
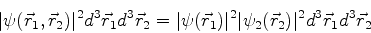 |
(704) |
e a probabilidade do evento composto (partícula  aqui e
partícula
aqui e
partícula 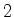 ali) é o produto das probabilidades dos eventos
individuais, o que caracteriza, na linguagem das probabilidades, a
independência dos eventos.
ali) é o produto das probabilidades dos eventos
individuais, o que caracteriza, na linguagem das probabilidades, a
independência dos eventos.
Se as partículas interagem, essas probabilidades não são mais
independentes, e a função de onda do sistema composto não é mais
o produto das funções de onda dos sistemas elementares.
Sejam
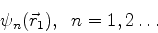 |
(705) |
funções que formam uma base do espaço 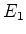 de estados da partícula
de estados da partícula  , e
, e
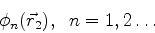 |
(706) |
funções que formam uma base do espaço 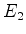 de estados da partícula
de estados da partícula 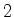 .
Consideremos o conjunto dos produtos
.
Consideremos o conjunto dos produtos
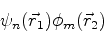 |
(707) |
para todos os valores possíveis de 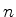 e
e 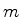 . O conjunto de todas
as combinações lineares, com coeficientes complexos, desses produtos,
é um espaço vetorial30. Os elementos desse
espaço vetorial são, então, expressões da forma
. O conjunto de todas
as combinações lineares, com coeficientes complexos, desses produtos,
é um espaço vetorial30. Os elementos desse
espaço vetorial são, então, expressões da forma
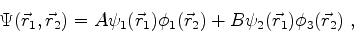 |
(708) |
por exemplo. Mais geralmente,
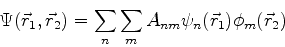 |
(709) |
onde os 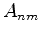 são números complexos.
são números complexos.
O produto escalar neste espaço é definido assim: para elementos da
base,
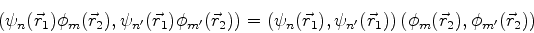 |
(710) |
A extensão a um elemento geral é feita usando a bilinearidade do
produto escalar, isto é,
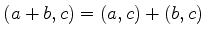 |
|
|
(711) |
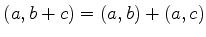 |
|
|
(712) |
Desta maneira,
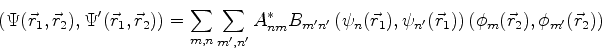 |
(713) |
onde
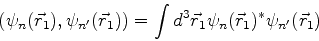 |
(714) |
e assim por diante.
Os mesmos resultados se aplicam no caso de se ter, em lugar de duas ou
mais partículas, dois ou mais conjuntos de variáveis
independentes. Por exemplo, uma partícula livre no espaço
tridimensional, descrita por coordenadas cartesianas. As coordenadas
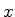 ,
, 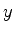 e
e 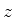 são independentes, e a função de onda da partícula
é escrita, num estado de momento definido,
são independentes, e a função de onda da partícula
é escrita, num estado de momento definido,
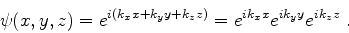 |
(715) |
Outro caso semelhante é o do spin. Na mecânica quântica
não-relativística (e na ausência de campos magnéticos) as
coordenadas espaciais e as variáveis de spin são independentes:
a probabilidade de um elétron estar em uma determinada posição e
ter, por exemplo, componente 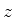 do spin igual a +1/2, é o produto
das duas probabilidades. A função de onda de um elétron é então
o produto
do spin igual a +1/2, é o produto
das duas probabilidades. A função de onda de um elétron é então
o produto
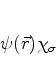 |
(716) |
onde 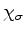 é uma das duas matrizes coluna
é uma das duas matrizes coluna
e 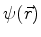 é a função de onda espacial.
é a função de onda espacial.
Se o hamiltoniano de um sistema for constituído de um termo
que depende das coordenadas espaciais e outro que depende das
variáveis de spin, por exemplo
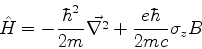 |
(717) |
com 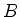 constante, o elemento de matriz de
constante, o elemento de matriz de 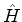 entre dois
estados do tipo que aparece na eq.(717), é
entre dois
estados do tipo que aparece na eq.(717), é
A extensão deste formalismo para um número arbitrário de
partículas é óbvio, e fica ao encargo do leitor.
Como um exemplo final, vamos examinar de novo o átomo de hidrogênio, mas sob
um aspecto mais realista: a interação de uma partícula de massa  e carga
+
e carga
+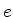 , o próton, com um elétron de massa
, o próton, com um elétron de massa 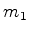 e carga -
e carga -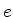 . O nosso tratamento anterior
deste mesmo problema considerava a massa do proton (que é cerca de 2000 vezes maior que a do
elétron) como infinita, desprezando, assim, a reação do elétron sobre o proton. Uma descrição mais
acurada do problema, então, considera um sistema de duas partículas ligadas por um potencial
coulombiano. Sejam
. O nosso tratamento anterior
deste mesmo problema considerava a massa do proton (que é cerca de 2000 vezes maior que a do
elétron) como infinita, desprezando, assim, a reação do elétron sobre o proton. Uma descrição mais
acurada do problema, então, considera um sistema de duas partículas ligadas por um potencial
coulombiano. Sejam 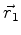 e
e 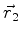 as posições do elétron e do próton,
respectivamente. O potencial coulombiano será da forma
as posições do elétron e do próton,
respectivamente. O potencial coulombiano será da forma
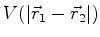 , e a
equação de Schrödinger será
, e a
equação de Schrödinger será
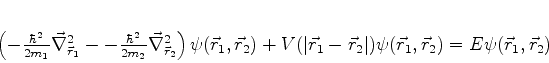 |
(719) |
Introduzimos as novas variáveis
sendo as transformações inversas dadas por
com 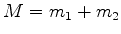 .
.
Reconhecemos 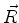 como a posição do centro-de-massa, na mecânica clássica. A outra
variável,
como a posição do centro-de-massa, na mecânica clássica. A outra
variável, 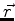 , é, obviamente, a posição do elétro em relação ao próton. Na mecânica
clássica sabemos que essas variáveis são independentes: enquanto o movimento relativo pode
complicar-se à vontade, o centro-de-massa segue serenamente seu movimento retilíneo e uniforme.
Isto nos sugere, na mecânica quântica, procurar soluções da equação de Schrödinger (720)
que sejam produtos de uma função de
, é, obviamente, a posição do elétro em relação ao próton. Na mecânica
clássica sabemos que essas variáveis são independentes: enquanto o movimento relativo pode
complicar-se à vontade, o centro-de-massa segue serenamente seu movimento retilíneo e uniforme.
Isto nos sugere, na mecânica quântica, procurar soluções da equação de Schrödinger (720)
que sejam produtos de uma função de 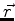 por uma função de
por uma função de 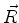 . Mas, primeiro, vamos
escrever (720) em termos dessas novas variáveis. Após um cálculo não muito
complicado, descrito abaixo em letras mais miúdas, obtemos, para (720),
. Mas, primeiro, vamos
escrever (720) em termos dessas novas variáveis. Após um cálculo não muito
complicado, descrito abaixo em letras mais miúdas, obtemos, para (720),
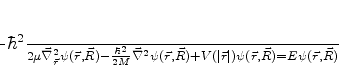 |
(724) |
Aqui aparece a nova variável  , a massa reduzida, definida por
, a massa reduzida, definida por
Procuremos agora soluções da forma
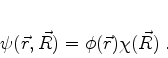 |
(725) |
Inserindo o segundo membro de (726) em (725) obtemos
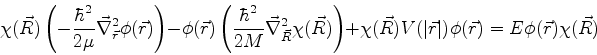 |
(726) |
que pode ser reescrita assim:
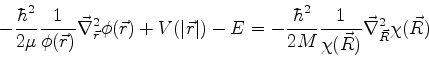 |
(727) |
O segundo membro não depende de 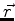 , e é igual ao primeiro membro, que não depende
de
, e é igual ao primeiro membro, que não depende
de 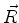 . Logo, o segundo membro não depende nem de
. Logo, o segundo membro não depende nem de 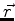 nem de
nem de 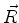 , ou seja,
é constante. O primeiro membro, por consegüinte, é também constante. Logo,
, ou seja,
é constante. O primeiro membro, por consegüinte, é também constante. Logo,
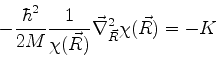 |
(728) |
com 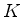 constante. Isto é a mesma coisa que
constante. Isto é a mesma coisa que
 |
(729) |
onde pusemos
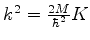 . Isto é permitido, com
. Isto é permitido, com 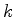 real, porque (730)
pode ser escrita
real, porque (730)
pode ser escrita
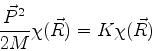 |
(730) |
com 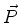 hermiteano. Logo,
hermiteano. Logo, 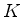 é positivo.
é positivo.
Voltando à eq.(730), sua solução é
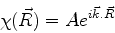 |
(731) |
com
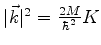 . Conclui-se que o centro-de-massa move-se como
uma partícula livre em estado de momento bem definido. Existe, portanto, um sistema de
referência inercial em que o centro-de-massa está em repouso.
. Conclui-se que o centro-de-massa move-se como
uma partícula livre em estado de momento bem definido. Existe, portanto, um sistema de
referência inercial em que o centro-de-massa está em repouso.
Para 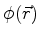 temos agora a equação
temos agora a equação
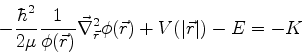 |
(732) |
ou
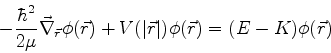 |
(733) |
Desta equação vemos que, àparte o movimento do centro-de-massa, o problema foi
reduzido a um problema de uma partícula, de massa  , que se move sob a ação
de um campo que lhe dá uma energia potencial
, que se move sob a ação
de um campo que lhe dá uma energia potencial 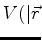 . A partir de agora basta
reproduzir, mutatis mutandis31, a solução anterior para o átomo de hidrogênio.
. A partir de agora basta
reproduzir, mutatis mutandis31, a solução anterior para o átomo de hidrogênio.
1. Calcule o raio médio (
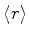 ) do ``átomo de hidrogênio
muônico'', em que o elétron foi substituído por um
) do ``átomo de hidrogênio
muônico'', em que o elétron foi substituído por um 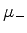 , uma partícula que
tem as mesma propriedades eletromagnéticas que o elétron, a não ser a massa,
que é 480 vezes a massa do elétron.
, uma partícula que
tem as mesma propriedades eletromagnéticas que o elétron, a não ser a massa,
que é 480 vezes a massa do elétron.
2. Calcule o espectro, raio médio, e tudo que lhe ocorrer, do positrônio,
um ``átomo'' formado por um positron e um elétron. O pósitron tem a mesma massa
que o elétron, e a carga igual à do proton. Despreze o fenômeno de aniquilação
partícula-anti-partícula.
Henrique Fleming 2003
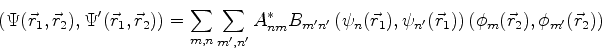
![]() ,
, ![]() e
e ![]() são independentes, e a função de onda da partícula
é escrita, num estado de momento definido,
são independentes, e a função de onda da partícula
é escrita, num estado de momento definido,
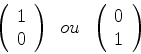
![$\displaystyle \chi_{+}^{\dagger}\left[\int
d^3\vec{r}\psi_{1}^*(\vec{r})\left(-\frac{\hbar^2}{2m}\vec{\nabla^2}\right)\psi_{2}(\vec{r})
\right]\chi_{-}$](img2062.png)
![$\displaystyle \frac{e\hbar}{2mc}B\int
d^3\vec{r}\psi_1^*(\vec{r})\psi_2(\vec{r})\left[\chi_{+}^{\dagger}\sigma_z\chi_{-}\right]$](img2063.png)
![$\displaystyle \left[\chi_{+}^{\dagger}\chi_{-}\right]\left[\int
d^3\vec{r}\psi_...
...vec{r})\left(-\frac{\hbar^2}{2m}\vec{\nabla^2}\right)\psi_{2}(\vec{r})
\right]+$](img2064.png)
![$\displaystyle \left[\chi_{+}^{\dagger}\sigma_z\chi_{-}\right]\left[\frac{e\hbar}{2mc}B\int
d^3\vec{r}\psi_1^*(\vec{r})\psi_2(\vec{r})\right]$](img2065.png)
![]() e carga
+
e carga
+![]() , o próton, com um elétron de massa
, o próton, com um elétron de massa ![]() e carga -
e carga -![]() . O nosso tratamento anterior
deste mesmo problema considerava a massa do proton (que é cerca de 2000 vezes maior que a do
elétron) como infinita, desprezando, assim, a reação do elétron sobre o proton. Uma descrição mais
acurada do problema, então, considera um sistema de duas partículas ligadas por um potencial
coulombiano. Sejam
. O nosso tratamento anterior
deste mesmo problema considerava a massa do proton (que é cerca de 2000 vezes maior que a do
elétron) como infinita, desprezando, assim, a reação do elétron sobre o proton. Uma descrição mais
acurada do problema, então, considera um sistema de duas partículas ligadas por um potencial
coulombiano. Sejam ![]() e
e ![]() as posições do elétron e do próton,
respectivamente. O potencial coulombiano será da forma
as posições do elétron e do próton,
respectivamente. O potencial coulombiano será da forma
![]() , e a
equação de Schrödinger será
, e a
equação de Schrödinger será
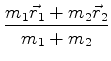
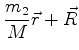
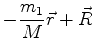
![]() como a posição do centro-de-massa, na mecânica clássica. A outra
variável,
como a posição do centro-de-massa, na mecânica clássica. A outra
variável, ![]() , é, obviamente, a posição do elétro em relação ao próton. Na mecânica
clássica sabemos que essas variáveis são independentes: enquanto o movimento relativo pode
complicar-se à vontade, o centro-de-massa segue serenamente seu movimento retilíneo e uniforme.
Isto nos sugere, na mecânica quântica, procurar soluções da equação de Schrödinger (720)
que sejam produtos de uma função de
, é, obviamente, a posição do elétro em relação ao próton. Na mecânica
clássica sabemos que essas variáveis são independentes: enquanto o movimento relativo pode
complicar-se à vontade, o centro-de-massa segue serenamente seu movimento retilíneo e uniforme.
Isto nos sugere, na mecânica quântica, procurar soluções da equação de Schrödinger (720)
que sejam produtos de uma função de ![]() por uma função de
por uma função de ![]() . Mas, primeiro, vamos
escrever (720) em termos dessas novas variáveis. Após um cálculo não muito
complicado, descrito abaixo em letras mais miúdas, obtemos, para (720),
. Mas, primeiro, vamos
escrever (720) em termos dessas novas variáveis. Após um cálculo não muito
complicado, descrito abaixo em letras mais miúdas, obtemos, para (720),
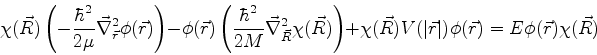
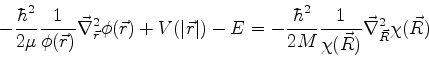
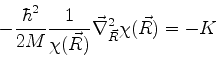
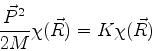
![]() temos agora a equação
temos agora a equação
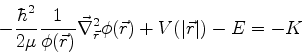
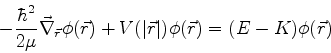
![]() em termos de
em termos de ![]() e
e ![]() , a mesma tarefa devendo ser realizada também para
, a mesma tarefa devendo ser realizada também para
![]() . Trabalhando com as componentes ao longo do eixo
. Trabalhando com as componentes ao longo do eixo ![]() já podemos adivinhar a expressão geral. Temos
já podemos adivinhar a expressão geral. Temos