Next: Sistemas compostos Up: Mecânica Quântica Previous: Perturbação periódica próxima à Sumário Índice Remissivo
Van der Waals interpretou a constante ![]() como o volume ocupado pelos átomos: em gases
rarefeitos este volume pode ser desprezado. A constante
como o volume ocupado pelos átomos: em gases
rarefeitos este volume pode ser desprezado. A constante ![]() estava associada, segundo ele, a
uma força atrativa entre dois átomos. O próprio van der Waals sugeriu, mais tarde, um potencial
de interação da forma
estava associada, segundo ele, a
uma força atrativa entre dois átomos. O próprio van der Waals sugeriu, mais tarde, um potencial
de interação da forma
Mais tarde ainda Keesom obteve o potencial
Contudo, gases de moléculas não polares também apresentam valores não-nulos para a
constante ![]() , de modo que uma força mais geral do que a de Keesom
seria necessária.
, de modo que uma força mais geral do que a de Keesom
seria necessária.
Como se sabe, o grande sucesso da equação de estado de van der Waals baseia-se essencialmente na hipótese de uma força atrativa entre as moléculas. Essas forças causam, em adição à pressão externa, uma pressão interna que é proporcional ao quadrado da densidade. De acordo com van der Waals, estas forças de atração existem entre moléculas de qualquer tipo, e constituem uma propriedade geral da matéria. Parece, por isso, de particular interesse considerar a origem dessa atração universal.
Sabe-se hoje com certeza absoluta que a molécula é um sistema de cargas elétricas, e somos levados a procurar uma origem elétrica para as forças de van der Waals. Será certamente desnecessário considerar detalhes da estrutura molecular. Uma propriedade da matéria tão geral quanto a atração de van der Waals não pode requerer, para a sua explicação, mais do que aspectos estruturais, comuns a todas as moléculas. Mostraremos no que se segue que, de fato, é suficiente saber que as moléculas são sistemas elétricos em que as cargas não estão rigidamente presas às suas posições em repouso. Uma relação entre a constante de atração de van der Waals, de um lado, e o índice de refração e o alargamento das linhas espectrais, do outro lado, pode ser deduzida na base dessa hipótese.
Em termos gerais, na realização dese processo de média, a probabilidade de uma orientação arbitrária teria de ser determinada em base ao princípio de Boltzmann-Maxwell. Quanto mais alta a temperatura, porém, menos importante é a dependência na energia mútua. No limite de altas temperaturas, todas as orientações serão igualmente prováveis. Obviamente, a hipótese de van der Waals requer que a característica coesão introduzida na equação persista no caso limite.
Pode ser mostrado facilmente que dois sistemas elétricos rígidos, em média, não exercem força um sobre o outro. O potencial que é gerado em um ponto distante por uma molécula pode ser considerado como originando-se de uma série de esferas concêntricas cobertas por uma camada de cargas elétricas de densidade superficial constante. Se as moléculas assumem todas as possíveis orientações no espaço, cada carga ocupa, na média, todos os pontos da esfera com igual freqüência. Como é sabido qye uma esfera com densidade superficial de carga constante afeta pontos de seu esterior como se a carga total estivesse concentrada no centro, e como a molécula possui carga total zero, a média do potencial no ponto considerado será zero. Assim, não existe força efetiva na média, entre duas moléculas rígidas.
A situação é imediata e essencialmente mudada se se consideram
moléculas que não são completamente rígidas. O fato de que cada gás
tem um índice de refração diferente de 1 é prova da mobilidade das
cargas separadas da molécula. Levando isto em consideração, será claro
que uma dada molécula adquire um momento elétrico de dipolo no campo
![]() de outra molécula, e o valor desse momento é proporcional a
de outra molécula, e o valor desse momento é proporcional a
![]() . Assim, surge uma energia mútua entre as duas moléculas que é
proporcional ao produto do momento de dipolo pelo campo
. Assim, surge uma energia mútua entre as duas moléculas que é
proporcional ao produto do momento de dipolo pelo campo
![]() , ou
seja, é quadrática em
, ou
seja, é quadrática em
![]() . Conseqüentemente, a força média não
pode se anular. Além disso, pode ser visto prontamente que essa força
é sempre de atração. Assim, podemos concluir que descobrimos a força
que está na origem da atração universal de van der
Waals29
. Conseqüentemente, a força média não
pode se anular. Além disso, pode ser visto prontamente que essa força
é sempre de atração. Assim, podemos concluir que descobrimos a força
que está na origem da atração universal de van der
Waals29
A situação pode ser ilustrada pelo exemplo seguinte. Dois dipolos
estão situados em oposição um ao outro.
{0.5}
\pscircle[...
...$}
\uput[0](4.5,5.5){{\Large I}}
\uput[0](4.5,2){{\Large II}}
\end{pspicture}](img1879.png)
(b)Na posição II. Aqui o efeito principal é atrativo. O campo agora desloca as cargas de modo que os momentos crescem. O efeito principal é agora aumentado, ou, dito de outra forma, de novo uma força atrativa foi adicionada como efeito secundário.
O efeito principal se anula quando se faz a média sobre todas as orientações. Como o efeito secundário é sempre positivo, ele nunca se anulará na média.
Atá aqui as palavras de Debye. Como já mencionamos, este efeito que ele descreve efetivamente existe, mas não é suficiente: os gases nobres têm átomos essencialmente indeformáveis, e, no entanto, se condensam, sob a ação da atração de van der Waals. Falta ainda alguma coisa.
Em 1930, Fritz London(Zeitschrift für Physik,63,245(1930)) utilizou a teoria
quântica das perturbações para obter o potencial de interação
A seguir mostraremos que a força de van der Waals, na forma obtida por London, pode ser atribuída à energia do ponto zero.
http://nobelprize.org/nobel_prizes/physics/laureates/1910/waals-lecture.html http://nobelprize.org/nobel_prizes/physics/laureates/1910/waals-bio.html
Mais curiosidades sobre as forças de van der Waals:
http://news.nationalgeographic.com/news/2002/08/0828_020828_gecko.html http://www.bbc.co.uk/dna/h2g2/A6378230 http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Debye-1920/Debye-1920.html
De grande interêsse e atualidade é o artigo de S. K. Lamoureux, ``Casimir forces: Still surprising after 60 years'', Physics Today,Fevereiro de 2007, pg.40, que considera a força de van der Waals no contexto mais amplo das forças de Casimir. Em particular, menciona-se neste artigo o fato de que a aderência que permite às lagartixas subir uma parede de vidro é devida à força de van der Waals.
Daí, no entanto, se concluiria que átomos ou moléculas de estados fundamentais esfericamente simétricos (e, portanto, sem dipolos ou quadrupolos permanentes), como os gases inertes, não deveriam apresentar coesão, contrariamente à experiência.
Uma solução para este problema foi apresentada por Fritz London (1930), que mostrou que a deformabilidade tem um segundo efeito, característico da mecãnica quântica. De acordo com esta teoria, existe um "movimento do ponto zero", isto é, mesmo no estado de mínima energia o átomo ou molécula apresentam movimento de cargas, de modo que pode existir um dipolo oscilante, com a freqüência do elétron. Aproximados os átomos um do outro, os "movimentos do ponto zero" dos dipolos agem sempre de modo que o resultado seja uma atração.
Para descrever a interação entre dois átomos de hidrogênio de forma bem simples,
consideremos cada um deles como um núcleo positivo de carga ![]() e um elétron, de carga
e um elétron, de carga
![]() que, por ação de um campo eletromagntico, está oscilando harmônicamente em torno
do núcleo fixo. No primeiro semestre mostramos que, num modelo muito simples do átomo,
se o elétron é deslocado de uma
distância
que, por ação de um campo eletromagntico, está oscilando harmônicamente em torno
do núcleo fixo. No primeiro semestre mostramos que, num modelo muito simples do átomo,
se o elétron é deslocado de uma
distância ![]() em relação ao núcleo, aparece sobre ele uma força restitutiva da forma
em relação ao núcleo, aparece sobre ele uma força restitutiva da forma
Supondo os dois átomos idênticos, cada um deles terá, então, por causa da
deformação, uma energia potencial
elástica, ou seja, teremos energias potenciais
![]() para um
átomo (
para um
átomo (![]() é o deslocamento do elétron em relação ao átomo) e
é o deslocamento do elétron em relação ao átomo) e
![]() para o outro.
para o outro.
Os núcleos dos átomos estão à distância ![]() um do outro. Supondo, apenas para fixar
as idéias, que o átomo à esquerda tenha o elétron deslocado para a esquerda,
e que o da direita tenha o seu deslocamento para a direita, teremos uma energia potencial
elétrica dada por
um do outro. Supondo, apenas para fixar
as idéias, que o átomo à esquerda tenha o elétron deslocado para a esquerda,
e que o da direita tenha o seu deslocamento para a direita, teremos uma energia potencial
elétrica dada por
Podemos então, na Eq.(654), expandir cada termo que contenha ![]() e
e
![]() em série de potências de
em série de potências de ![]() , o que se faz sem dificuldade usando
a fórmula do binômio. Por exemplo,
, o que se faz sem dificuldade usando
a fórmula do binômio. Por exemplo,
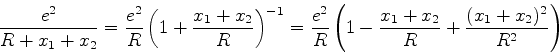
A energia total do sistema é então dada por
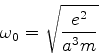
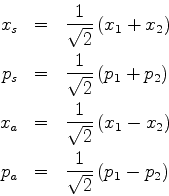
| (658) |
O estado fundamental desse sistema, que é a energia mais baixa que este
sistema de dipólos pode ter, é obtido pondo ![]() (é a energia do ponto
zero do sistema). Mesmo que não haja nenhum campo externo atuando sobre o sistema,
ele terá esta energia, pelo menos. Ela é
(é a energia do ponto
zero do sistema). Mesmo que não haja nenhum campo externo atuando sobre o sistema,
ele terá esta energia, pelo menos. Ela é
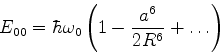 |
(660) |
Suponhamos que os núcleos de dois átomos de hidrogênio, um localizado na origem, o outro
no ponto com vetor de posição ![]() , estejam no eixo
, estejam no eixo ![]() . O elétron do primeiro
átomo está em
. O elétron do primeiro
átomo está em
![]() , e o do outro em
, e o do outro em
![]() .
.
{0.2}
\pscircle[li...
...
\uput[0](2.3,2){$\vec{r}_{1}$}
\uput[0](8.8,2){$\vec{r}_{2}$}
\end{pspicture}](img1929.png)
O hamiltoniano
para este sistema será escrito
Os átomos não perturbados estão em seus estados fundamentais, de sorte que o autoestado
de ![]() é dado por
é dado por
| (668) |
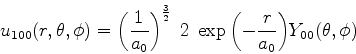
Para que o potencial ![]() possa ser tratado perturbativamente, suporemos o caso
em que
possa ser tratado perturbativamente, suporemos o caso
em que ![]() , onde
, onde ![]() é o raio de Bohr, o que acarreta que
é o raio de Bohr, o que acarreta que
![]() e
e
![]() são ambos muito menores do que 1.
são ambos muito menores do que 1.
Neste caso, expandindo ![]() em potências de
em potências de ![]() (com o uso da fórmula do
binômio de Newton) teremos, após vários cancelamentos, e desprezando termos da ordem
de
(com o uso da fórmula do
binômio de Newton) teremos, após vários cancelamentos, e desprezando termos da ordem
de ![]() e menores,
e menores,
Olhando, na eq.(665), a expressão para ![]() , que denotaremos por
, que denotaremos por ![]() , temos
, temos
é possível (A. Unsold, 43,563(1927)) obter um limite superior para a quantidade positiva
![]() , substituíndo, em (671), todos os
, substituíndo, em (671), todos os ![]() (com
(com ![]() ) pela energia
do estado excitado mais baixo para o qual
) pela energia
do estado excitado mais baixo para o qual
![]() é diferente de
zero. Vamos denotá-la por
é diferente de
zero. Vamos denotá-la por ![]() . De fato, neste caso teremos
. De fato, neste caso teremos
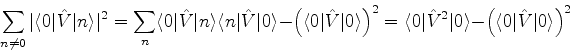 |
(671) |
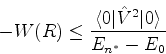 |
(672) |
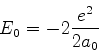
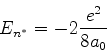
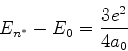 |
(673) |
| (674) |
| (675) |
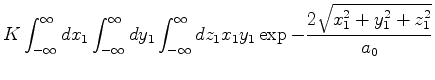 |
|||
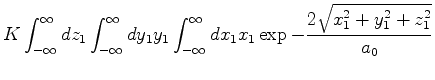 |
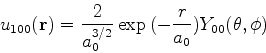
As autofunções da energia de ![]() , denotadas por
, denotadas por
![]() , satisfarão
, satisfarão
As funções de onda e níveis de energia perturbados serão escritos
Nas segunda das equações acima, podemos substituir
Nas equações (690) e seguintes, tomemos o produto escalar, termo a
termo, por ![]() . Tomemos como exemplo a terceira delas. Teremos
. Tomemos como exemplo a terceira delas. Teremos
Por outro lado, ![]() pode ser expandida nas autofunções não perturbadas,
pode ser expandida nas autofunções não perturbadas,
Henrique Fleming 2003