Considere a perturbação periódica
de freqüência 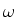 tal que
tal que
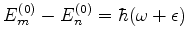 onde
onde  é pequeno.
A equação básica é (604),
é pequeno.
A equação básica é (604),
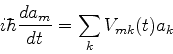 |
(621) |
com
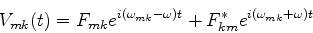 |
(622) |
Esta expressão contém expoentes de tamanhos diversos, um dos quais,  ,
é particularmente pequeno, aparecendo nas combinações
,
é particularmente pequeno, aparecendo nas combinações
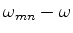 e
e
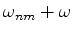 . Como a solução de (604) envolve uma integração
do segundo membro no tempo, usaremos o fato de que, quando um integrando possui
vários termos oscilantes, a contribuição dominante é a daquele termo que oscila
menos. A base matemática rigorosa para isto é o lema de Riemann-Lebesgue28. Podemos, então,
aproximar as equações (604) por
. Como a solução de (604) envolve uma integração
do segundo membro no tempo, usaremos o fato de que, quando um integrando possui
vários termos oscilantes, a contribuição dominante é a daquele termo que oscila
menos. A base matemática rigorosa para isto é o lema de Riemann-Lebesgue28. Podemos, então,
aproximar as equações (604) por
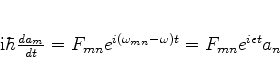 |
(623) |
e
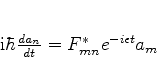 |
(624) |
Introduzindo a quantidade auxiliar
temos, para (624),
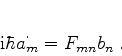 |
(625) |
Substituindo, em (625), 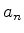 em termos de
em termos de  ,
ficamos com
,
ficamos com
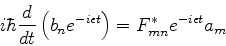 |
(626) |
ou
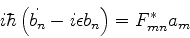 |
(627) |
Derivando mais uma vez,
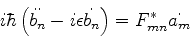 |
(628) |
que, usada em (626), dá
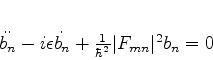 |
(629) |
Trata-se agora de resolver esta equação diferencial linear
a coeficientes constantes. Para isto existe um algoritmo
bem conhecido: como todas as soluções de equações deste tipo
podem ser escritas como exponenciais, procura-se a solução
como uma exponencial genérica, escrita como
com 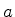 a determinar. Temos
a determinar. Temos
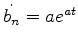 e
e
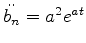 . Inserindo estas expressões em
(630) e cancelando a exponencial comum, obtemos
. Inserindo estas expressões em
(630) e cancelando a exponencial comum, obtemos
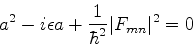 |
(630) |
que é um equação do segundo grau. As soluções são
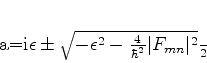 |
(631) |
Para simplificar esta expressão introduzimos algumas abreviações:
Usando esta notação as soluções (632) podem ser
escritas
e, portanto,
Como
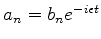 , obtemos
, obtemos
Finalmente, introduzindo
chegamos a
onde, para obter as duas últimas, usamos a eq.(625).
Note-se que um par (
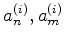 ) representa uma função de
onda
) representa uma função de
onda
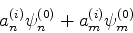 |
(640) |
A solução mais geral é dada por uma combinação linear dessas soluções,
para 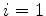 e
e 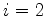 . Como cada uma já foi escrita com uma constante
multiplicativa arbitrária, temos
. Como cada uma já foi escrita com uma constante
multiplicativa arbitrária, temos
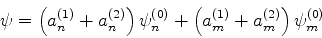 |
(641) |
ou
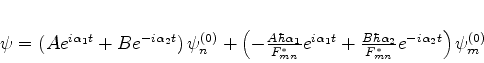 |
(642) |
Como condição inicial, queremos que, para 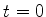 ,
,
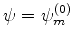 .
Tomando
.
Tomando 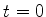 na eq.(643), vemos que devemos ter
na eq.(643), vemos que devemos ter
Conseqüentemente,
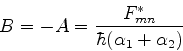 |
(645) |
Note-se ainda que
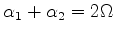 . A expressão para
. A expressão para
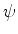 é, então:
é, então:
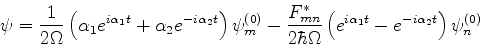 |
(646) |
O coeficiente de
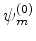 na equação anterior, depois de alguma álgebra,
é escrito:
na equação anterior, depois de alguma álgebra,
é escrito:
![\begin{displaymath}
e^{-i\frac{\epsilon}{2}t}\left[\cos{\Omega t}-\frac{i\epsilon}{2\Omega}
\sin{\Omega t}\right]
\end{displaymath}](img1864.png) |
(647) |
e o de
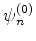 dá
dá
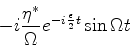 |
(648) |
de modo que
![\begin{displaymath}
\psi=e^{-i\frac{\epsilon}{2}t}\left[\left(\cos{\Omega t}-\f...
...i\frac{\eta^*}{\Omega}\sin{\Omega t}\;
\psi_{n}^{(0)}\right]
\end{displaymath}](img1866.png) |
(649) |
O sistema inicia (em 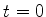 ) no estado
) no estado
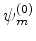 . A probabilidade de ele
estar, no instante
. A probabilidade de ele
estar, no instante 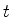 , no estado
, no estado
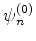 , é dada pelo quadrado do
módulo do coeficiente de
, é dada pelo quadrado do
módulo do coeficiente de
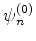 , que é
, que é
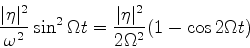 |
(650) |
Na ressonância, isto é, para 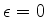 , temos
, temos
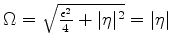 , logo,
a probabilidade da transição é dada por
, logo,
a probabilidade da transição é dada por
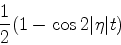 |
(651) |
que varia periodicamente entre 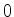 e
e  . Isto significa que,
na ressonância, o sistema realiza transições periódicas
entre
. Isto significa que,
na ressonância, o sistema realiza transições periódicas
entre
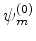 e
e
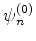 . Note que a
freqüência dessas transições não depende de nenhuma das
freqüências presentes: ela é determinada por
. Note que a
freqüência dessas transições não depende de nenhuma das
freqüências presentes: ela é determinada por 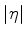 , ou
seja, pela intensidade da perturbação.
Henrique Fleming 2003
, ou
seja, pela intensidade da perturbação.
Henrique Fleming 2003
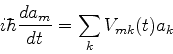
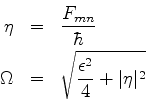
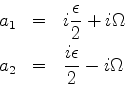
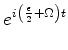
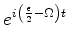
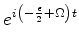
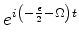
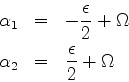
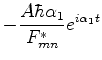
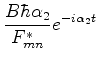
![]() ) representa uma função de
onda
) representa uma função de
onda
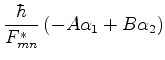
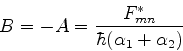
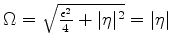 , logo,
a probabilidade da transição é dada por
, logo,
a probabilidade da transição é dada por