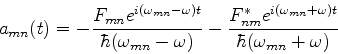Até agora estudamos o efeito de pequenas perturbações sobre um sistema físico,
sob a hipótese de que essas perturbações fossem independentes do tempo, como um campo
magnético constante, etc. Muito importante para o estudo das propriedades de átomo
é investigar o que acontece com ele quando, por exemplo, uma onda eletromagnética
o atinge. A luz do Sol, por exemplo, é um campo eletromagnético que varia muito
rapidamente mas que, em condições normais, é muito menos intenso do que os campos elétricos
e magnéticos do próprio átomo. Então a luz é uma perturbação, mas uma perturbação
dependente do tempo.
Seja
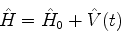 |
(594) |
o hamiltoniano perturbado, escrito como a soma de um hamiltoniano 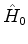 ,
não-perturbado, sobre o qual sabemos tudo, e de uma perturbação
,
não-perturbado, sobre o qual sabemos tudo, e de uma perturbação 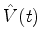 ,
onde a perturbação, agora, depende do tempo. Esta é uma dependência
explícita no tempo. Vamos explicar por meio de um exemplo: suponha dois elétrons,
interagindo sob a ação de seus campos elétricos. A repulsão eletrostática
fará com que, à medida que o tempo passa, eles estejam cada vez mais longe
um do outro. Portanto, do ponto-de-vista de cada um dos elétrons, o campo
do outro varia com o tempo. Não se trata desta dependência no tempo, conseqüência
do movimento, o que estamos estudando aqui. Trata-se de uma dependência no tempo
adicional a esta, e que aconteceria, por exemplo, se a carga de um dos elétrons
fosse aumentando com o tempo. Se os dois elétrons estivessem no interior de um capacitor
cujo campo elétrico fosse alterável por meio de um reostato, teríamos um campo
com dependência explícita no tempo. Uma onda de luz que incide sobre um elétron,
já citada acima, é outro exemplo de perturbação com dependência explícita
no tempo. Neste caso, não há conservação da energia 27
e o hamiltoniano perturbado não terá, em geral, estados estacionários. Supõe-se,
porém, que o hamiltoniano
,
onde a perturbação, agora, depende do tempo. Esta é uma dependência
explícita no tempo. Vamos explicar por meio de um exemplo: suponha dois elétrons,
interagindo sob a ação de seus campos elétricos. A repulsão eletrostática
fará com que, à medida que o tempo passa, eles estejam cada vez mais longe
um do outro. Portanto, do ponto-de-vista de cada um dos elétrons, o campo
do outro varia com o tempo. Não se trata desta dependência no tempo, conseqüência
do movimento, o que estamos estudando aqui. Trata-se de uma dependência no tempo
adicional a esta, e que aconteceria, por exemplo, se a carga de um dos elétrons
fosse aumentando com o tempo. Se os dois elétrons estivessem no interior de um capacitor
cujo campo elétrico fosse alterável por meio de um reostato, teríamos um campo
com dependência explícita no tempo. Uma onda de luz que incide sobre um elétron,
já citada acima, é outro exemplo de perturbação com dependência explícita
no tempo. Neste caso, não há conservação da energia 27
e o hamiltoniano perturbado não terá, em geral, estados estacionários. Supõe-se,
porém, que o hamiltoniano 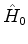 os tenha, e o objetivo é calcular as funções de
onda do sistema perturbado como correções aos estados estacionários do sistema
não-perturbado.
os tenha, e o objetivo é calcular as funções de
onda do sistema perturbado como correções aos estados estacionários do sistema
não-perturbado.
Sejam
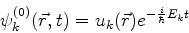 |
(595) |
as funções de onda dos estados estacionários do sistema não-perturbado.
Então uma solução arbitrária da equação de Schrödinger para o sistema
não-perturbado pode ser escrita na forma
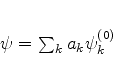 |
(596) |
Vamos agora procurar uma solução da equação perturbada
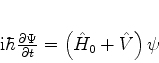 |
(597) |
na forma de uma soma
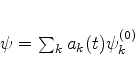 |
(598) |
onde os 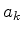 agora, diferentemente daqueles da Eq.(597),
são funções do tempo.
Para ser mais esoecífico, seja
agora, diferentemente daqueles da Eq.(597),
são funções do tempo.
Para ser mais esoecífico, seja  a função de onda do sistema perturbado
que é uma correção da função de onda não perturbada
a função de onda do sistema perturbado
que é uma correção da função de onda não perturbada
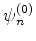 . A equação
(599) é agora escrita assim:
. A equação
(599) é agora escrita assim:
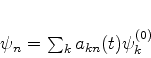 |
(599) |
Levando a Eq.(600) à Eq.(598),
e lembrando que as
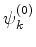 satisfazem a equação
satisfazem a equação
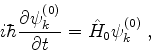 |
(600) |
obtemos
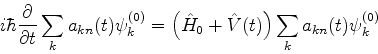 |
(601) |
ou
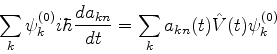 |
(602) |
Multiplicando ambos os lados da equação à esquerda por
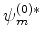 e integrando, temos
e integrando, temos
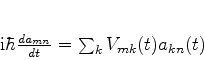 |
(603) |
onde
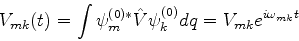 |
(604) |
com
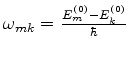 , são os elementos de matriz da
perturbação, incluíndo as exponenciais que contêm a dependência temporal. Deve-se
notar ainda que, como
, são os elementos de matriz da
perturbação, incluíndo as exponenciais que contêm a dependência temporal. Deve-se
notar ainda que, como 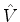 depende explicitamente do tempo, as quantidades
depende explicitamente do tempo, as quantidades 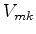 são também funções do tempo.
O fato de que
são também funções do tempo.
O fato de que  é próxima de
é próxima de
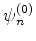 é expresso por
é expresso por
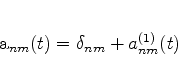 |
(605) |
Inserindo (606) em (604), temos
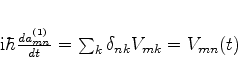 |
(606) |
Note-se que
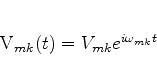 |
(607) |
A equação (607) pode então, por causa de (608),
ser escrita:
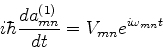 |
(608) |
Integrando, obtém-se:
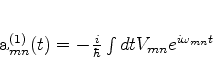 |
(609) |
O caso mais importante é de uma perturbação com dependência periódica
no tempo,
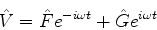 |
(610) |
à qual devemos, evidentemente, impôr a condição de hermiticidade.
Como
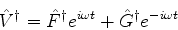 |
(611) |
e
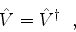 |
(612) |
segue que
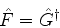 |
(613) |
Para os elementos de matriz, temos a relação:
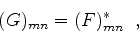 |
(614) |
ou seja,
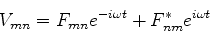 |
(615) |
Usando isto em (610), temos
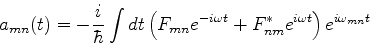 |
(616) |
ou
 |
(617) |
e, integrando,
 |
(618) |
ou ainda,
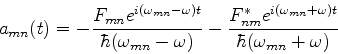 |
(619) |
Esta expressão assinala que alguma coisa importante acontece quando
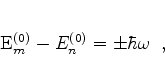 |
(620) |
embora, estritamente, a teoria de perturbações não se aplique neste caso,
já que os efeitos são grandes. Em todo o caso, é claro que a ação de um
campo perturbador de freqüência dada por (621) é muito mais
intensa do que para quaisquer outras freqüências. Este fenômeno é denominado
ressonância.
Henrique Fleming 2003
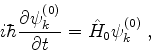
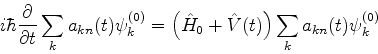
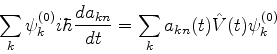
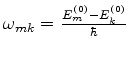 , são os elementos de matriz da
perturbação, incluíndo as exponenciais que contêm a dependência temporal. Deve-se
notar ainda que, como
, são os elementos de matriz da
perturbação, incluíndo as exponenciais que contêm a dependência temporal. Deve-se
notar ainda que, como