Subsections
Recomendamos ao leitor, neste ponto, a leitura do Apêndice Matemático 1,
que se encontra no fim destas notas.
Vimos que o nível 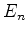 do átomo de hidrogênio tem uma
degenerescência de ordem
do átomo de hidrogênio tem uma
degenerescência de ordem  . Isto é, existem
. Isto é, existem  estados
diferentes do átomo de hidrogênio com energia
estados
diferentes do átomo de hidrogênio com energia 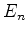 (se contarmos
o spin, serão
(se contarmos
o spin, serão 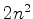 ). Quando se aplica um campo externo ao átomo, pode
acontecer de esses estados interagirem de maneira diferente com o campo,
e então a degenerescência é quebrada: em lugar de um nível
passaremos a ter vários, possivelmente até
). Quando se aplica um campo externo ao átomo, pode
acontecer de esses estados interagirem de maneira diferente com o campo,
e então a degenerescência é quebrada: em lugar de um nível
passaremos a ter vários, possivelmente até 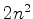 , se o campo externo
for suficientemente complicado. Diz-se, então, que a degenerescência
foi removida.
, se o campo externo
for suficientemente complicado. Diz-se, então, que a degenerescência
foi removida.
Não podemos aplicar cegamente os resultados obtidos até aqui pelo
seguinte motivo: a correção de primeira ordem à função de onda não-perturbada
que obtivemos,
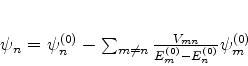 |
(528) |
contém, no caso de níveis degenerados, situações em que
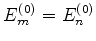 ,
para
,
para 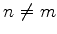 , ou seja, na fórmula acima, apareceriam denominadores nulos.
Para obter as correções correspondentes para níveis degenerados, precisamos
de uma adaptação do método anterior a esta nova situação. Para evitar um
excesso de índices, vamos reobter as fórmulas básicas sob forma ligeiramente
diferente.
, ou seja, na fórmula acima, apareceriam denominadores nulos.
Para obter as correções correspondentes para níveis degenerados, precisamos
de uma adaptação do método anterior a esta nova situação. Para evitar um
excesso de índices, vamos reobter as fórmulas básicas sob forma ligeiramente
diferente.
Seja 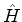 o hamiltoniano perturbado, e vamos escrevê-lo em uma série
de potências de um parâmetro pequeno,
o hamiltoniano perturbado, e vamos escrevê-lo em uma série
de potências de um parâmetro pequeno, 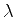 , desta forma[10]:
, desta forma[10]:
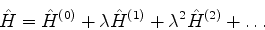 |
(529) |
Note-se que, no nosso tratamento anterior, o termo 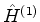 era denotado
por
era denotado
por 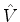 , e os demais,
, e os demais, 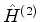 ,
, 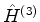 , etc, eram
omitidos. Aqui são incluídos mais por razões estéticas do que por real
utilidade. É claro que o
, etc, eram
omitidos. Aqui são incluídos mais por razões estéticas do que por real
utilidade. É claro que o 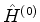 daqui é o
daqui é o 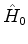 do
tratamento anterior.
do
tratamento anterior.
Seja 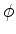 a função de onda perturbada, que queremos calcular. Será escrita
também como uma série de potências em
a função de onda perturbada, que queremos calcular. Será escrita
também como uma série de potências em 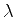 :
:
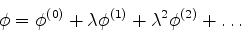 |
(530) |
e também para a energia se escreverá
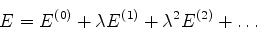 |
(531) |
A equação de Schrödinger para as quantidades perturbadas é
 |
(532) |
que, pelo uso das expansões acima, se escreve
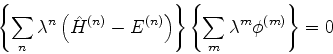 |
(533) |
ou, por extenso,
| |
|
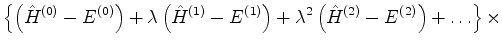 |
|
| |
|
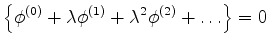 |
(534) |
Igualando a zero os coeficientes da várias potências de 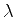 , temos
, temos
e assim por diante.
Da primeira, tiramos, evidentemente, que
que é a equação de autovalores do hamiltoniano não-perturbado, por hipótese
já completamente resolvida.
Na segunda, Eq.(537), multiplicamos à esquerda por
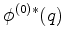 e integramos, obtendo
e integramos, obtendo
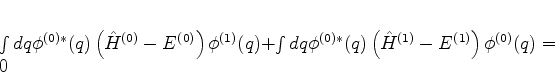 |
(538) |
Mas, pela hermiticidade de 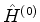 , temos
, temos
![\begin{displaymath}
\int dq \phi^{(0) *}(q)\left(\hat{H}^{(0)}-E^{(0)}\right)\...
...}^{(0)}-E^{(0)}\right)\phi^{(0)}(q)\right]^*
\phi^{(1)}(q)=0
\end{displaymath}](img1570.png) |
(539) |
Logo, de (539),
ou
de acordo com o resultado obtido anteriormente.
Suponhamos que o nível 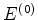 seja
seja 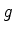 -vezes degenerado. Isto é,
existem
-vezes degenerado. Isto é,
existem 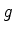 funções
funções
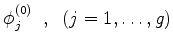 tais que
tais que
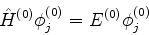 |
(540) |
Neste caso, qualquer combinação linear desses
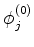 será
também uma função de onda de energia
será
também uma função de onda de energia 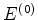 . De fato,
. De fato,
A idéia do método é esta: procurar as combinações lineares
das funções
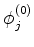 que sejam tais que o efeito da perturbação
em primeira ordem seja pequeno. À luz da Eq.(529), isto significa que,
para compensar os denominadores que se anulam, quando
que sejam tais que o efeito da perturbação
em primeira ordem seja pequeno. À luz da Eq.(529), isto significa que,
para compensar os denominadores que se anulam, quando
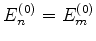 com
com
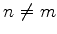 , devemos escolher as combinações lineares das
, devemos escolher as combinações lineares das
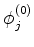 que
fazem o numerador correspondente também se anular26. Suponhamos o problema resolvido, e seja
que
fazem o numerador correspondente também se anular26. Suponhamos o problema resolvido, e seja
 |
(541) |
a combinação linear procurada.
Note-se que supomos as
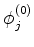 normalizadas. Então a
normalizadas. Então a 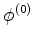 da
Eq.(542) será normalizada se
da
Eq.(542) será normalizada se
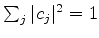 .
.
Considere a equação
![\begin{displaymath}
\left[\hat{H}^{(0)}-E^{(0)}\right]\phi^{(1)} +
\left[\hat{H}^{(1)}-E^{(1)}\right]\phi^{(0)}=0
\end{displaymath}](img1582.png) |
(542) |
ou
![\begin{displaymath}
\left[\hat{H}^{(0)}-E^{(0)}\right]\phi^{(1)} +
\left[\hat{...
...m_{j^{\prime}=1}^{g}c_{j^{\prime}}
\phi_{j^{\prime}}^{(0)}=0
\end{displaymath}](img1583.png) |
(543) |
Multiplicando à esquerda por
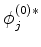 e integrando, obtém-se:
e integrando, obtém-se:
![\begin{displaymath}
\int dq \phi_{j}^{(0) *}(q)\left[\hat{H}^{(0)}-E^{(0)}\righ...
...ht]\sum_{j^{\prime}}
c_{j^{\prime}}\phi_{j^{\prime}}^{(0)}=0
\end{displaymath}](img1585.png) |
(544) |
O primeiro termo do primeiro membro é zero, usando-se a hermiticidade de
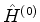 , como na Eq.(540). Então segue que
, como na Eq.(540). Então segue que
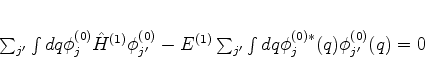 |
(545) |
e, introduzindo o símbolo
podemos escrever (546) como
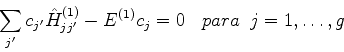 |
(546) |
ou ainda,
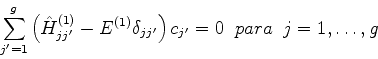 |
(547) |
Este é um sistema de 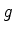 equações homogêneas a
equações homogêneas a 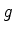 incógnitas (os coeficientes
incógnitas (os coeficientes 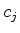 ),
cuja solução trivial é
),
cuja solução trivial é 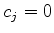 para todo
para todo 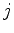 . É claro que esta solução
não tem nenhum interesse físico. Para que existam outras soluções, é necessário
que
. É claro que esta solução
não tem nenhum interesse físico. Para que existam outras soluções, é necessário
que
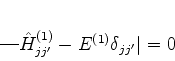 |
(548) |
onde, se 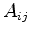 é uma matriz,
é uma matriz, 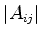 é o determinante da matriz.
é o determinante da matriz.
A equação (549) é denominada, por razões históricas,
equação secular. Vamos a um exemplo. Para 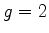 , a matriz em questão é
, a matriz em questão é
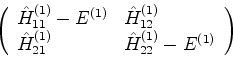 |
(549) |
A equação secular então dá:
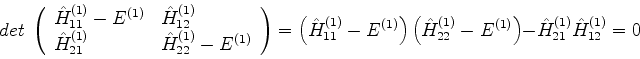 |
(550) |
ou
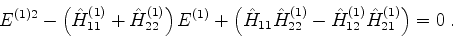 |
(551) |
Há duas soluções,
Logo, o nível de energia 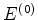 se desdobra em dois, de energia s
se desdobra em dois, de energia s
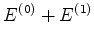 e
e
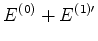 .
.
De uma maneira geral, se a degenerescência for de ordem 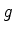 , teremos uma equação
algébrica de ordem
, teremos uma equação
algébrica de ordem 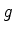 , com
, com 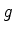 soluções para
soluções para 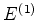 . Se forem todas diferentes,
o nível se desdobrará em
. Se forem todas diferentes,
o nível se desdobrará em 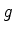 novos níveis, e a degenerescência será
completamente removida.
novos níveis, e a degenerescência será
completamente removida.
Como aplicação vamos calcular a ação de uma campo magnético fraco sobre o estado
fundamental do átomo de hidrogênio. Sabe-se que quando se liga um campo magnético externo,
o nível 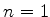 , que corresponde ao estado fundamental, desdobra-se em um par de níveis.
A interpretação física é a seguinte: devido ao spin, o elétron comporta-se como um
pequeno ímã. A energia de interação de um dipolo magnético de momento de dipolo
, que corresponde ao estado fundamental, desdobra-se em um par de níveis.
A interpretação física é a seguinte: devido ao spin, o elétron comporta-se como um
pequeno ímã. A energia de interação de um dipolo magnético de momento de dipolo
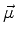 com um campo magnético
com um campo magnético 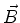 é
é
e depende, portanto, da orientação relativa dos dois. Como o spin quântico só pode
ter duas orientações, correspondentes às componentes 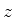 iguais a
iguais a
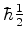 ou
ou
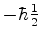 , há dois valores possíveis para a energia
, há dois valores possíveis para a energia 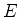 , que, grosso
modo, é adicionada à energia do estado fundamental. Surgem assim os dois níveis.
Este fenômeno chama-se efeito Zeeman anômalo.
, que, grosso
modo, é adicionada à energia do estado fundamental. Surgem assim os dois níveis.
Este fenômeno chama-se efeito Zeeman anômalo.
Esta interpretação superficial é confirmada por uma análise mais cuidadosa, baseada
no cálculo perturbativo.
Vimos na equação (456) que o termo de interação do elétron no estado
fundamental do átomo de hidrogênio (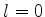 ), é
), é
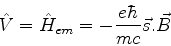 |
(554) |
onde 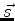 é o operador de spin, cuja representação matricial na base
formada pelos estados
é o operador de spin, cuja representação matricial na base
formada pelos estados
é, por exemplo, para a componente 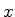 ,
,
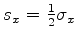 , com
, com
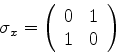 |
(557) |
Levando-se em conta o spin, o estado fundamental é degenerado, e, por isso,
é preciso utilizar o formalismo desenvolvido especialmente para este caso.
Como só o spin interessa neste caso, vamos denotar por
 o
elemento de matriz genérico entre autoestados da projeção
o
elemento de matriz genérico entre autoestados da projeção 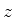 do spin. Para
dar um exemplo não excessivamente trivial, tomaremos o eixo
do spin. Para
dar um exemplo não excessivamente trivial, tomaremos o eixo 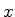 ao longo da direção
do campo magnético, suposto uniforme e constante no tempo.
ao longo da direção
do campo magnético, suposto uniforme e constante no tempo.
O termo de interação é então dado pela matriz
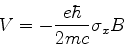 |
(558) |
cujos elementos são
Usando agora as equações (553) e (554),
obtemos
Logo, a diferença de energia entre os dois níveis, uma vez
removida a degenerescência, é
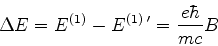 |
(564) |
em muito bom acordo com a experiência, para campos magnéticos fracos.
1. No fim desta lista há uma tabela de valores de
quantidades como a carga e massa do elétron, velocidade da luz,
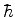 , etc. Consulte-a para resolver as questões que seguem.
, etc. Consulte-a para resolver as questões que seguem.
(a)Calcule, em 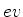 (eletronvolts) o potencial de ionização do
átomo de hidrogênio,
que é a energia necessária para extrair um elétron do estado
fundamental.
(eletronvolts) o potencial de ionização do
átomo de hidrogênio,
que é a energia necessária para extrair um elétron do estado
fundamental.
(b)Calcule, em 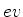 , a diferença de energia entre o estado fundamental e o
primeiro estado excitado do átomo de hidrogênio.
, a diferença de energia entre o estado fundamental e o
primeiro estado excitado do átomo de hidrogênio.
(c) Calcule a razão entre
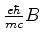 e as quantidades calculadas
acima, sendo
e as quantidades calculadas
acima, sendo 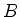 o campo magnético da Terra. Isto dará uma idéia
do tamanho do efeito Zeeman anômalo (ver Notas) em relação
a duas energia s típicas do átomo de hidrogênio.
o campo magnético da Terra. Isto dará uma idéia
do tamanho do efeito Zeeman anômalo (ver Notas) em relação
a duas energia s típicas do átomo de hidrogênio.
2. Considere o poço quadrado infinito que estudamos em detalhe: duas
paredes inpenetráveis, paralelas, a uma distância 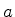 uma da outra.
Calcule o efeito sobre o estado fundamental de uma mola de constante
elástica muito pequena que prende a partícula à parede em
uma da outra.
Calcule o efeito sobre o estado fundamental de uma mola de constante
elástica muito pequena que prende a partícula à parede em 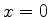 :
correção à energia e à função de onda, até primeira ordem.
:
correção à energia e à função de onda, até primeira ordem.
3. Mesmo problema, mas, agora, o movimento da partícula no poço
é afetado por uma força constante muito fraca, da esquerda para
a direita.
4. Qual é a dificuldade em introduzir a ``resistência do
ar'', isto é, uma força proporcional à velocidade, dessa forma?
5. Efeito Stark no átomo de hidrogênio: uma perturbação dada por
um potencial eletrostático
onde 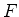 é o módulo de campo elétrico, age sobre o átomo. Calcule
os novos níveis de energia com
é o módulo de campo elétrico, age sobre o átomo. Calcule
os novos níveis de energia com 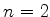 . Resposta:
. Resposta:
1 erg =
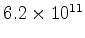 eV
eV
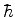 =
=
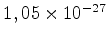 erg.s
erg.s
c =
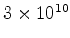 cm/s
cm/s
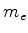 =
=
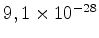 g
g
Magneton de Bohr (
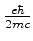 )=
)=
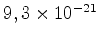 erg/gauss
erg/gauss
Campo magnético da Terra 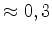 gauss.
gauss.
6.O próton não é um ponto. Uma representação aceitável
para ele é como uma esfera de raio 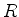 muito menor do que o raio
do átomo. Quando calculamos os estados estacionários do átomo de
hidrogênio, supusemos o próton como um ponto. Seja
muito menor do que o raio
do átomo. Quando calculamos os estados estacionários do átomo de
hidrogênio, supusemos o próton como um ponto. Seja 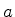 o raio do
átomo. Para
o raio do
átomo. Para
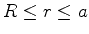 , a energia potencial do elétron é a
mesma, seja o próton um ponto ou uma esfera de raio
, a energia potencial do elétron é a
mesma, seja o próton um ponto ou uma esfera de raio 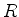 . Mas no
intervalo
. Mas no
intervalo
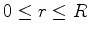 , a energia potencial do elétron é
diferente. Calcule o efeito da extensão do próton sobre os níveis
de energia do átomo de hidrogênio considerando como perturbação a
diferença de energia potencial devida à extensão do próton. Mais
precisamente:
, a energia potencial do elétron é
diferente. Calcule o efeito da extensão do próton sobre os níveis
de energia do átomo de hidrogênio considerando como perturbação a
diferença de energia potencial devida à extensão do próton. Mais
precisamente:
(a)Mostre que o potencial perturbador é
(b)Calcule a correção à energia do estado fundamental. De quantos
por cento é alterada?
7. Considere um oscilador linear unidimensional de massa 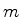 e
carga
e
carga 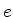 . Sua energia potencial é escrita como
. Sua energia potencial é escrita como
e a energia irradiada é desprezível. Um campo elétrico fraco,
constante no espaço e no tempo, é aplicado na direção 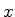 . Mostre
que,
. Mostre
que,
(a) Em primeira ordem de perturbação, os níveis de energia não são
alterados.
(b) Calcule a correção em segunda ordem para o estado
fundamental.
(c) Resolva o problema exatamente, e mostre que a solução exata
coincide com (b).
(d) Analise o problema clássico eqüivalente e compare as soluções
exatas para o problema não-perturbado e perturbado.
8.A linha espectral de
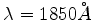 do mercúrio resulta da
transição de um estado excitado para o estado fundamental
do mercúrio resulta da
transição de um estado excitado para o estado fundamental
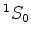 . Um campo magnético de
. Um campo magnético de 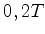 divide essa linha em três
componentes com uma separação de
divide essa linha em três
componentes com uma separação de 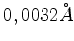 entre linhas
vizinhas. O que se pode dizer do estado excitado?
entre linhas
vizinhas. O que se pode dizer do estado excitado?
9. (Dedicado a Douglas Cancherini) Correções relativistas aos níveis atômicos.
A energia de uma partícula relativista livre é dada pela conhecida expressão
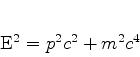 |
(565) |
A parte desta energia que permanece quando 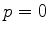 é dita ``energia de repouso'', e é dada pela
famosíssima expressão
é dita ``energia de repouso'', e é dada pela
famosíssima expressão
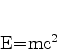 |
(566) |
A diferença entre as energia s dadas por (566) e (567) é
a energia cinética da partícula. A eq.(566) pode ser escrita
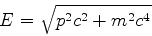 |
(567) |
e, na maioria dos casos, o termo que descreve a energia em repouso é muito maior do que o outro.
Então podemos proceder assim:
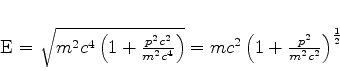 |
(568) |
que pode ser calculada aproximadamente usando a fórmula do binômio de Newton:
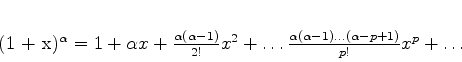 |
(569) |
Usando (570) em (569), temos
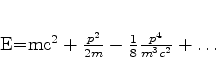 |
(570) |
Subtraíndo a energia de repouso de (571), temos uma expressão para a energia cinética
que já inclui algumas correções relativistas, pois a energia cinética não-relativista é
dada por
 .
.
Calculamos os níveis de energia do átomo de hidrogênio resolvendo a equação de Schrödinger para
estados estacionários com o hamiltoniano
 |
(571) |
Para avaliar a importância das correções relativistas, podemos utilizar a teoria das perturbações,
considerando como perturbação
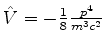 .
.
(a) Obtenha a Eq.(571).
(b) Calcule a correção à energia do estado fundamental de um átomo hidrogenóide de 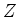 qualquer,
e exiba a dependência em
qualquer,
e exiba a dependência em 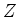 . Para que valor de
. Para que valor de 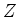 se teria uma correção de
se teria uma correção de 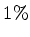 ?
1. Considere o poço quadrado infinito usual, com paredes
impenetráveis em
?
1. Considere o poço quadrado infinito usual, com paredes
impenetráveis em 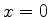 e
e 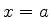 . Calcule o efeito sobre a energia de um estado
estacionário qualquer de uma mola de constante elástica muito pequena
(a energia potencial perturbadora deve ser muito menor do que a separação
entre os níveis) que prende a partícula à parede em
. Calcule o efeito sobre a energia de um estado
estacionário qualquer de uma mola de constante elástica muito pequena
(a energia potencial perturbadora deve ser muito menor do que a separação
entre os níveis) que prende a partícula à parede em 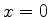 , em primeira
ordem de perturbação.
, em primeira
ordem de perturbação.
Solução: os níveis de energia não-perturbados são:
com
sendo a função de onda correspondente
A perturbação é dada por
e a separação de níveis é
A condição de validade da teoria da perturbação, mencionada acima,
é (mostre!)
Note-se que a condição depende do nível. Uma perturbação pequena para
os níveis baixos pode não o ser para níveis altos.
A correção à energia é
Para 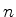 inteiro a integral
inteiro a integral
Obtém-se assim, para a correção,
Efeito Stark no átomo de hidrogênio: uma perturbação
dada por um potencial eletrostático
onde 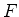 , constante, é o módulo do campo elétrico, age sobre
o átomo. Calcule os novos níveis de energia com
, constante, é o módulo do campo elétrico, age sobre
o átomo. Calcule os novos níveis de energia com 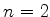 .
.
Solução: o nível 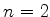 é degenerado, de ordem 4. As funções de
onda correspondentes são:
é degenerado, de ordem 4. As funções de
onda correspondentes são: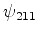 ,
, 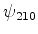 ,
, 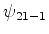 ,
,
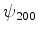 . Vamos denotar os elementos de matriz de
. Vamos denotar os elementos de matriz de 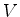 por
por
e assim por diante.
A equação secular é:
Um elemento de matriz típico é
Muitas dessas integrais são nulas por causa do seguinte fato:
se
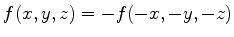 , então
, então
A troca de 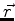 por
por 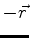 , ou seja, de (
, ou seja, de (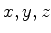 ) por
) por 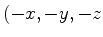 )
chama-se inversão espacial. Em coordenadas esféricas esta transformação é:
)
chama-se inversão espacial. Em coordenadas esféricas esta transformação é:
Em relação à inversão espacial, os harmônicos esféricos têm a
seguinte transformação (veja a prova abaixo):
Em conseqüência, as seguintes integrais são nulas:
pois
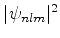 é par e
é par e 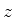 é ímpar, ou seja, o integrando é ímpar,
sendo o intervalo de integraçãop simétrico, pois é o espaço todo. Logo,
na equação secular, os elementos de matriz diagonais são todos nulos.
é ímpar, ou seja, o integrando é ímpar,
sendo o intervalo de integraçãop simétrico, pois é o espaço todo. Logo,
na equação secular, os elementos de matriz diagonais são todos nulos.
Na realidade, o mesmo fenômeno acontece com os elementos de matriz de 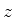 entre
estados de mesmo
entre
estados de mesmo 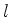 , por exemplo:
, por exemplo:
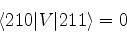
A matriz se simplifica para
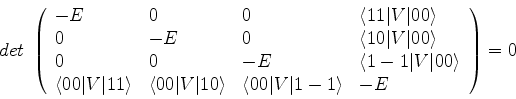
Esta equação dá
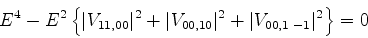
que tem como soluções 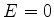 ,
, 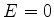 e
e
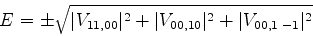
Finalmente, notando que ![$[V,l_z]=0$](img1696.png) , é fácil provar (veja a prova abaixo)
que os elementos de matriz de
, é fácil provar (veja a prova abaixo)
que os elementos de matriz de 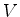 entre estados de valores distintos de
entre estados de valores distintos de 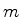 são nulos. Em conseqüência,
são nulos. Em conseqüência,

Usando as funções de onda
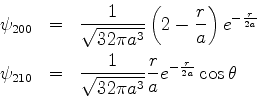
mostre que os demais valores de 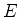 são:
são:
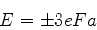
A conclusão é que o nível 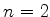 divide-se em três níveis: um, com
a mesma energia anterior, que é ainda degenerado (de ordem 2),
outro com energia igual à energia de Bohr adicionada de
divide-se em três níveis: um, com
a mesma energia anterior, que é ainda degenerado (de ordem 2),
outro com energia igual à energia de Bohr adicionada de 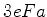 , e
um terceiro, com a energia de Bohr subtraída de
, e
um terceiro, com a energia de Bohr subtraída de 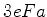 .
.
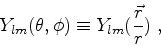
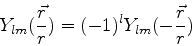
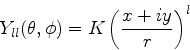
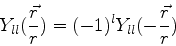
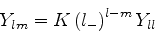
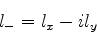
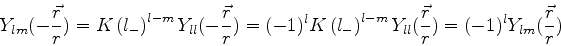
![\begin{eqnarray*}
0 & = & \langle l,m\vert[V,l_z]\vert l^{\prime},m^{\prime}\ra...
...gle -
m\langle l,m\vert V\vert l^{\prime},m^{\prime}\rangle =0
\end{eqnarray*}](img1714.png)
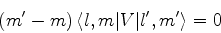
![\begin{eqnarray*}
0 & = & \int dq Y_{l^{\prime},m^{\prime}}^{*}[V,l_z]Y_{lm}\ ...
...= & (m-m^{\prime})\int dq Y_{l^{\prime},m^{\prime}}^{*}V Y_{lm}
\end{eqnarray*}](img1718.png)
1. Efeito Stark do estado fundamental do átomo de
hidrogênio
O elétron do átomo de hidrogênio acha-se sob a ação de um campo
elétrico externo que lhe confere uma energia potencial 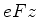 .
.
(a) Mostre que o efeito Stark para o nível 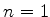 é, em primeira ordem
de perturbação, nulo.
é, em primeira ordem
de perturbação, nulo.
(b) Calcule a contribuição de segunda ordem, levando o cálculo até
onde puder.
(c) A partir de
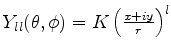 ,
calcule
,
calcule
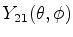 , determinando também a constante de
normalização.
, determinando também a constante de
normalização.
2.O átomo dos pobres
Um elétron está preso dentro de uma esfera ôca de paredes impenetráveis, de
raio 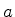 . Não há outras forças agindo sobre ele.
. Não há outras forças agindo sobre ele.
(a) Existem estados estacionários esfericamente simétricos?
(b) Determine os autovalores da energia desses estados.
(c) Determine a função de onda do estado esfericamente simétrico de
menor energia .
(d) Existem estados estacionários desse elétron que não sejam
esfericamente simétricos?
3. Oscilador preso a uma parede
Uma partícula de massa 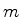 possui a energia potencial
possui a energia potencial
(a) Escreva o hamiltoniano para este sistema. e determine as autofunções
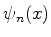 e autovalores
e autovalores 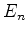 .
(b) Calcule o valor esperado
.
(b) Calcule o valor esperado
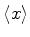 para o estado fundamental deste
sistema e compare com o valor da mesma quantidade para o oscilador verdadeiro.
Comente a diferença.
(c) Mesma coisa para
para o estado fundamental deste
sistema e compare com o valor da mesma quantidade para o oscilador verdadeiro.
Comente a diferença.
(c) Mesma coisa para
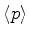 .
.
4. Um sistema físico tem, num certo instante, uma função de onda cuja única
dependência em 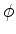 (quando expressa em coordenadas esféricas) é dada por
um fator
(quando expressa em coordenadas esféricas) é dada por
um fator
(a) Quais os possíveis valores para uma medida de 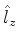 ?
?
(b)Qual o valor médio
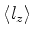 ?
Átomo dos pobres
?
Átomo dos pobres
O laplaceano em coordenadas esféricas pode ser escrito:
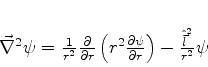 |
(572) |
onde
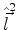 é o operador de momento angular total.
é o operador de momento angular total.
A equação de Schrödinger para estados estacionários do sistema
descrito é, então,
 |
(573) |
Procuremos soluções da forma
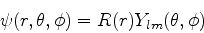 |
(574) |
Inserindo esta expressão em (574), temos, visto que
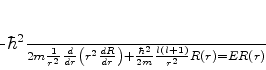 |
(575) |
Introduzindo a função 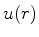 tal
tal 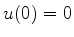 e
e
a equação (576) dá, para 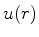 , a equação
, a equação
 |
(576) |
Para maior clareza, vamos apender o índice 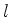 às soluções desta
equação. Então, reescrevemos:
às soluções desta
equação. Então, reescrevemos:
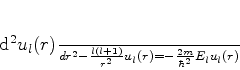 |
(577) |
Os ítens (a) e (b) podem ser respondidos imediatamente. Como as
soluções são da forma
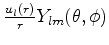 , as
eventuais soluções de simetria esférica têm de corresponder a
, as
eventuais soluções de simetria esférica têm de corresponder a
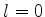 , já que o único harmônico esférico com esta simetria é o
, já que o único harmônico esférico com esta simetria é o
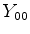 . A equação relevante é, então, (577) com
. A equação relevante é, então, (577) com
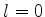 , ou seja,
, ou seja,
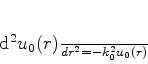 |
(578) |
onde pusemos
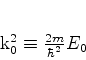 |
(579) |
A eq.(580) tem a solução geral
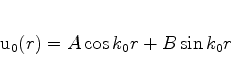 |
(580) |
mas, como 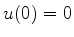 , devemos tomar
, devemos tomar 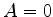 . Logo,
. Logo,
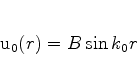 |
(581) |
Além disso, o átomo dos pobres tem raio 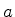 , e então a condição
adicional
, e então a condição
adicional 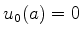 deve ser imposta. Com isto, obtemos
deve ser imposta. Com isto, obtemos
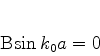 |
(582) |
cuja solução mais geral é
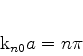 |
(583) |
onde 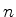 é um inteiro. Resolvemos, de novo para maior clareza,
apender um novo índice,
é um inteiro. Resolvemos, de novo para maior clareza,
apender um novo índice, 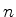 , às soluções. Temos, então, muitas
soluções esfericamente simétricas, caracterizadas por
, às soluções. Temos, então, muitas
soluções esfericamente simétricas, caracterizadas por
sendo as energia s dadas por
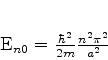 |
(585) |
Evidentemente a solução esfericamente simétrica de menor energia é
dada por 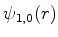 .
.
As demais questões sobre o átomo dos pobres podem ser resolvidas
sem dificuldade pelo leitor.
As soluções sem simetria esférica satisfazem a equação
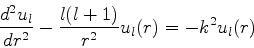 |
(586) |
Reescrevendo em termos da função
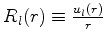 ,
temos
,
temos
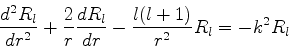 |
(587) |
As funções de Bessel esféricas são soluções da equação diferencial
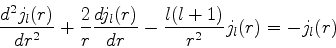 |
(588) |
de onde se deduz sem dificuldade que
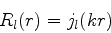 |
(589) |
Logo, as soluções sem simetria esférica têm a forma
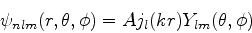 |
(590) |
A condição de contorno é
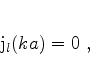 |
(591) |
que é satisfeita por certos valores de 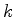 , denotados por
, denotados por 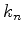 ,
para os quais (592) é satisfeita. Matematicamente,
trata-se então de fazer com que a quantidade
,
para os quais (592) é satisfeita. Matematicamente,
trata-se então de fazer com que a quantidade 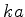 coincida com os
zeros da função de Bessel esférica
coincida com os
zeros da função de Bessel esférica 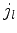 , que são
encontrados em tabelas. Sejam
, que são
encontrados em tabelas. Sejam
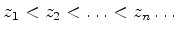 números tais que
números tais que
Então teremos
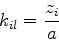 |
(592) |
sendo a energia deste estado estacionário dada por
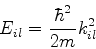 |
(593) |
Calcular as correções relativistas aos níveis
de energia como correções perturbativas. (Exercício 9, Seção
20.4 das notas de aula).
Solução: o hamiltoniano não-perturbado é
enquanto que o perturbado é, como vimos em aula,
A correção à energia em primeira ordem é, então,
Mas
e
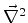 é um operador hermiteano (por que?). Então,
é um operador hermiteano (por que?). Então,
A equação de Schrödinger é
logo,
Logo,
Para a correção da energia temos, então,
ou,
Para uma análise qualitativa, podemos por:
Verifique cuidadosamente esses cálculos (foram feitos às pressas).
Em particular, verifique a validade de
Determine explicitamente a dependência total em 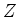 (há uma
escondida em
(há uma
escondida em 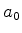 ?).
?).
Justifique o folklore que diz: correções relativistas são
importantes para núcleos pesados, em suas órbitas internas.
Como não há órbitas, que história é essa de ``órbitas
internas''?
Henrique Fleming 2003
![]() do átomo de hidrogênio tem uma
degenerescência de ordem
do átomo de hidrogênio tem uma
degenerescência de ordem ![]() . Isto é, existem
. Isto é, existem ![]() estados
diferentes do átomo de hidrogênio com energia
estados
diferentes do átomo de hidrogênio com energia ![]() (se contarmos
o spin, serão
(se contarmos
o spin, serão ![]() ). Quando se aplica um campo externo ao átomo, pode
acontecer de esses estados interagirem de maneira diferente com o campo,
e então a degenerescência é quebrada: em lugar de um nível
passaremos a ter vários, possivelmente até
). Quando se aplica um campo externo ao átomo, pode
acontecer de esses estados interagirem de maneira diferente com o campo,
e então a degenerescência é quebrada: em lugar de um nível
passaremos a ter vários, possivelmente até ![]() , se o campo externo
for suficientemente complicado. Diz-se, então, que a degenerescência
foi removida.
, se o campo externo
for suficientemente complicado. Diz-se, então, que a degenerescência
foi removida.
![]() o hamiltoniano perturbado, e vamos escrevê-lo em uma série
de potências de um parâmetro pequeno,
o hamiltoniano perturbado, e vamos escrevê-lo em uma série
de potências de um parâmetro pequeno, ![]() , desta forma[10]:
, desta forma[10]:
![]() a função de onda perturbada, que queremos calcular. Será escrita
também como uma série de potências em
a função de onda perturbada, que queremos calcular. Será escrita
também como uma série de potências em ![]() :
:
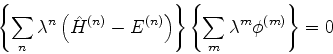
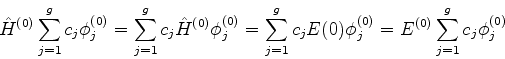
![\begin{displaymath}
\left[\hat{H}^{(0)}-E^{(0)}\right]\phi^{(1)} +
\left[\hat{...
...m_{j^{\prime}=1}^{g}c_{j^{\prime}}
\phi_{j^{\prime}}^{(0)}=0
\end{displaymath}](img1583.png)
![\begin{displaymath}
\int dq \phi_{j}^{(0) *}(q)\left[\hat{H}^{(0)}-E^{(0)}\righ...
...ht]\sum_{j^{\prime}}
c_{j^{\prime}}\phi_{j^{\prime}}^{(0)}=0
\end{displaymath}](img1585.png)
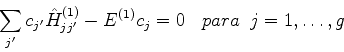
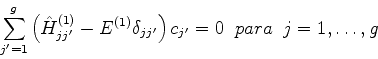
![]() , a matriz em questão é
, a matriz em questão é
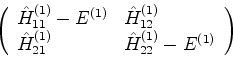
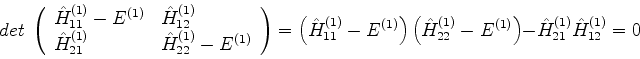
![]() , teremos uma equação
algébrica de ordem
, teremos uma equação
algébrica de ordem ![]() , com
, com ![]() soluções para
soluções para ![]() . Se forem todas diferentes,
o nível se desdobrará em
. Se forem todas diferentes,
o nível se desdobrará em ![]() novos níveis, e a degenerescência será
completamente removida.
novos níveis, e a degenerescência será
completamente removida.
![]() ), é
), é
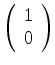
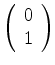
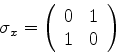
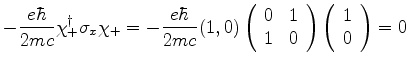
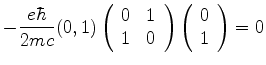
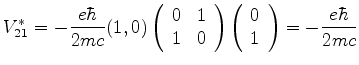
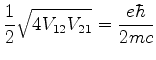
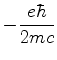
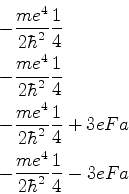
![]() eV
eV
![]() =
=
![]() erg.s
erg.s
![]() cm/s
cm/s
![]() =
=
![]() g
g
![]() )=
)=
![]() erg/gauss
erg/gauss
![]() gauss.
gauss.
![]() muito menor do que o raio
do átomo. Quando calculamos os estados estacionários do átomo de
hidrogênio, supusemos o próton como um ponto. Seja
muito menor do que o raio
do átomo. Quando calculamos os estados estacionários do átomo de
hidrogênio, supusemos o próton como um ponto. Seja ![]() o raio do
átomo. Para
o raio do
átomo. Para
![]() , a energia potencial do elétron é a
mesma, seja o próton um ponto ou uma esfera de raio
, a energia potencial do elétron é a
mesma, seja o próton um ponto ou uma esfera de raio ![]() . Mas no
intervalo
. Mas no
intervalo
![]() , a energia potencial do elétron é
diferente. Calcule o efeito da extensão do próton sobre os níveis
de energia do átomo de hidrogênio considerando como perturbação a
diferença de energia potencial devida à extensão do próton. Mais
precisamente:
, a energia potencial do elétron é
diferente. Calcule o efeito da extensão do próton sobre os níveis
de energia do átomo de hidrogênio considerando como perturbação a
diferença de energia potencial devida à extensão do próton. Mais
precisamente:
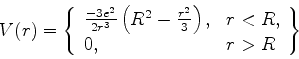
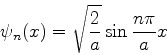
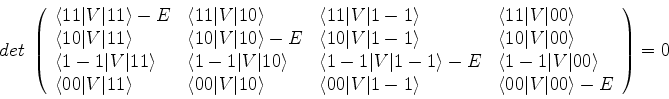
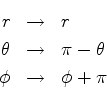
![]() entre
estados de mesmo
entre
estados de mesmo ![]() , por exemplo:
, por exemplo:
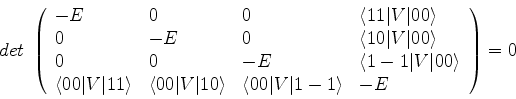
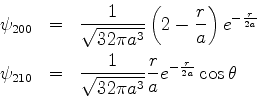
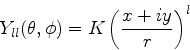
![\begin{eqnarray*}
0 & = & \langle l,m\vert[V,l_z]\vert l^{\prime},m^{\prime}\ra...
...gle -
m\langle l,m\vert V\vert l^{\prime},m^{\prime}\rangle =0
\end{eqnarray*}](img1714.png)
![\begin{eqnarray*}
0 & = & \int dq Y_{l^{\prime},m^{\prime}}^{*}[V,l_z]Y_{lm}\ ...
...= & (m-m^{\prime})\int dq Y_{l^{\prime},m^{\prime}}^{*}V Y_{lm}
\end{eqnarray*}](img1718.png)
![]() .
.
![]() é, em primeira ordem
de perturbação, nulo.
é, em primeira ordem
de perturbação, nulo.
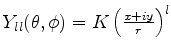 ,
calcule
,
calcule
![]() , determinando também a constante de
normalização.
, determinando também a constante de
normalização.
![]() . Não há outras forças agindo sobre ele.
. Não há outras forças agindo sobre ele.
![]() possui a energia potencial
possui a energia potencial
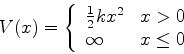
![]() , e então a condição
adicional
, e então a condição
adicional ![]() deve ser imposta. Com isto, obtemos
deve ser imposta. Com isto, obtemos
![]() .
.
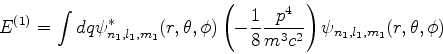

![]() (há uma
escondida em
(há uma
escondida em ![]() ?).
?).