Next: Teoria das perturbações Up: Mecânica Quântica Previous: O Spin Sumário Índice Remissivo
Seja ![]() um operador hermiteano, e
um operador hermiteano, e ![]() um estado do
sistema. Considere o operador
um estado do
sistema. Considere o operador
| (460) | |||
| (461) |
É imediato verificar que
| (462) | |||
| (463) |
Pela desigualdade de Cauchy-Schwartz, temos
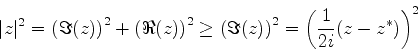
![\begin{displaymath}
\vert(\psi_{A},\psi_{B})\vert^2 \geq
\left(\frac{1}{2i}\left[(\psi_{A},\psi_{B})-(\psi_{B},\psi_{A})\right]\right)^2
\end{displaymath}](img1414.png)
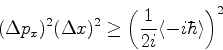
Exercício: determine ![]() e
e ![]() para o estado fundamental do átomo de hidrogênio. Mostre que:
para o estado fundamental do átomo de hidrogênio. Mostre que:
(a)
![]() .
.
(b)
![]() .
.
(c)
![]()
(d) Conclua que o movimento do elétron é ![]() o mínimo
possível compatível com as relações de incerteza.
o mínimo
possível compatível com as relações de incerteza.
A relação de incerteza energia -tempo é de natureza
fundamentalmente diferente daquela da relação de incerteza
posição-momento . Enquanto esta última é conseqüência
do fato de que os operadores
![]() e
e ![]() não
comutam, isto não acontece no caso da energia -tempo: nem mesmo existe um
operador ``tempo'' na mecânica quântica. O tempo que aparece na equação
de Schroedinger é o tempo marcado por qualquer relógio, e pode ser determinado,
em qualquer caso, com precisão arbitrária. O fato básico na obtenção
da desigualdade
não
comutam, isto não acontece no caso da energia -tempo: nem mesmo existe um
operador ``tempo'' na mecânica quântica. O tempo que aparece na equação
de Schroedinger é o tempo marcado por qualquer relógio, e pode ser determinado,
em qualquer caso, com precisão arbitrária. O fato básico na obtenção
da desigualdade
A relação de incerteza 469 deve ser interpretada assim: uma
medida perfeita da energia de um sistema (![]() ) leva um tempo infinito
(
) leva um tempo infinito
(
![]() ). A expressão 469 ensina
quanto deve durar, no mínimo, o processo de medida (a duração é
). A expressão 469 ensina
quanto deve durar, no mínimo, o processo de medida (a duração é
![]() ) para que a precisão obtida seja
) para que a precisão obtida seja ![]() .
.
Para obter 469, consideremos o processo de determinar a freqüência de uma onda. Matematicamente se sabe que a transformada de Fourier de uma onda nos dá a informação sobre quais freqüências participaram da construção da onda, por meio de superposição de ondas monocromáticas (isto é, de freqüências bem definidas).
Uma onda plana monocromática tem sua dependência temporal dada por
![]() , se sua freqüência for
, se sua freqüência for ![]() .23 Sua transformada
de Fourier é
.23 Sua transformada
de Fourier é
| (469) |
| (470) |
Na prática, porém, a medida da freqüência da onda
![]() é feita observando-se essa onda durante um intervalo de tempo finito, por
exemplo, do instante
é feita observando-se essa onda durante um intervalo de tempo finito, por
exemplo, do instante
![]() até o instante
até o instante
![]() .
Mas então a onda que realmente observamos é indistinguível
da seguinte onda
.
Mas então a onda que realmente observamos é indistinguível
da seguinte onda ![]() :
:
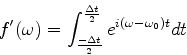 |
(472) |
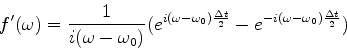 |
(473) |
![\begin{displaymath}
f'(\omega)=\Delta t \frac{\sin[(\omega-\omega_0)\frac{\Delta t}{2}]}
{(\omega-\omega_0)\frac{\Delta t}{2}}
\end{displaymath}](img1454.png) |
(474) |
| (475) |
| (476) |
| (477) |
| (478) |
| (479) |
Henrique Fleming 2003