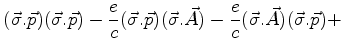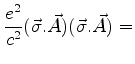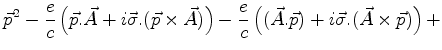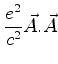Subsections
O Spin
Para introduzir o spin vamos apresentar um tratamento mais geral
do momento angular. No tratamento anterior, tínhamos obtido que os
autovalores  de
de 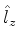 deviam ser números inteiros, sob o
argumento de que as autofunções de
deviam ser números inteiros, sob o
argumento de que as autofunções de 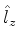 ,
,
deviam ser periódicas, de período 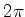 , na variável
, na variável 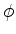 . Este
argumento não é rigoroso, pois a função de onda é determinada a
menos de uma fase. Retomaremos o problema agora. Descobriremos que
há novas possibilidades para os valores de
. Este
argumento não é rigoroso, pois a função de onda é determinada a
menos de uma fase. Retomaremos o problema agora. Descobriremos que
há novas possibilidades para os valores de  e
e 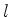 .
.
Para comodidade do leitor, repetiremos aqui alguns dos resultados
que obtivemos anteriormente para o momento angular.
Da relação
 concluímos que existe um valor máximo para o autovalor de
concluímos que existe um valor máximo para o autovalor de
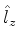 . Seja
. Seja 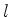 este valor máximo, e
este valor máximo, e 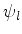 a autofunção
comum a
a autofunção
comum a
 e
e 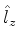 correspondente. Temos
correspondente. Temos
Logo,
Usando (385),
ou
Conclui-se que o autovalor de
 para a autofunção
para a autofunção
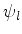 é
é  , onde
, onde 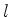 é o máximo valor possível para
é o máximo valor possível para
 . Pasaremos a denotar por
. Pasaremos a denotar por 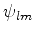 as autofunções comuns a
as autofunções comuns a
 e
e 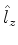 . Vamos determinar agora o menor
valor possível para
. Vamos determinar agora o menor
valor possível para  .
.
Em primeiro lugar, do fato de que
![$[\hat{\vec{l}}^2,\hat{l}_{-}]=0$](img1185.png) , segue que
, segue que
ou seja, o autovalor de
 é o mesmo para todos os
é o mesmo para todos os
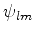 , com
, com 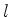 fixo.
fixo.
Seja 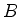 o mínimo valor de
o mínimo valor de  . Então
. Então
Esta última tem duas soluções,  , que é impossível, pois o
máximo valor de
, que é impossível, pois o
máximo valor de  é
é 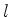 , e
, e 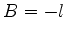 , que é o valor correto. Então,
, que é o valor correto. Então,
 está no intervalo
está no intervalo
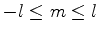 , e seus valores
sucessivos diferem de uma unidade: há, portanto,
, e seus valores
sucessivos diferem de uma unidade: há, portanto,  valores de
valores de
 , para
, para 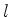 dado. Em conseqüência,
dado. Em conseqüência,  deve ser um número
inteiro, e temos duas possibilidades:(a)
deve ser um número
inteiro, e temos duas possibilidades:(a)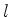 é inteiro, que é o
caso que já havíamos estudado. Costuma-se chamar esses momento s
angulares de momento angular orbital. (b)
é inteiro, que é o
caso que já havíamos estudado. Costuma-se chamar esses momento s
angulares de momento angular orbital. (b) 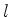 é um ímpar
dividido por dois (semi-inteiro, na gíria dos físicos). Este
tipo de momento angular é denominado spin. Temos, então,
spins
é um ímpar
dividido por dois (semi-inteiro, na gíria dos físicos). Este
tipo de momento angular é denominado spin. Temos, então,
spins  ,
, 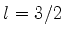 , etc.
, etc.
O caso mais importante do spin é aquele em que  . Neste caso,
. Neste caso,
 só pode ter os valores
só pode ter os valores 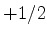 e
e 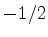 , e é conveniente tratar
os operadores de momento angular utilizando suas representações
matriciais. Para tanto, vamos determinar os elementos de matriz dos
operadores
, e é conveniente tratar
os operadores de momento angular utilizando suas representações
matriciais. Para tanto, vamos determinar os elementos de matriz dos
operadores  ,
, 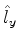 e
e 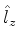 . Temos, usando a
notação de Dirac,
. Temos, usando a
notação de Dirac,
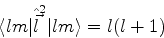 |
(385) |
e, como
Como todos esses elementos de matriz contêm o mesmo valor de 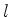 ,
podemos omitir este índice, ou seja, podemos abreviar a notação para:
,
podemos omitir este índice, ou seja, podemos abreviar a notação para:
etc.
Obviamente
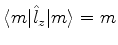 ,
,
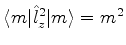 e
e
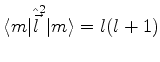 . Logo,
. Logo,
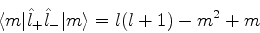 |
(386) |
ou
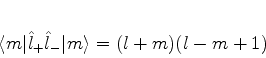 |
(387) |
A completude dos autoestados de 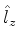 permite escrever
permite escrever
que, inserida em (388), dá
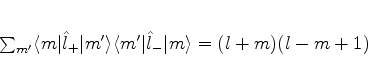 |
(388) |
e sabemos que
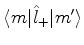 só é diferente
de zero se
só é diferente
de zero se 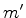 for igual a
for igual a 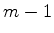 . Logo, (389) se escreve
. Logo, (389) se escreve
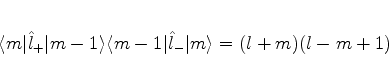 |
(389) |
Além disso,
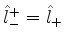 e
e
o que permite escrever, de (390),
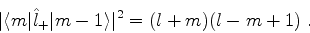 |
(390) |
Daí tiramos que
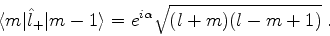 |
(391) |
A escolha de 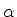 está ligada à definição precisa dos
harmônicos esféricos
está ligada à definição precisa dos
harmônicos esféricos
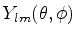 . Para a escolha
feita anteriormente, Eq.(329), deve-se escolher
. Para a escolha
feita anteriormente, Eq.(329), deve-se escolher 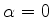 . Logo,
. Logo,
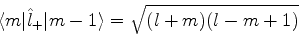 |
(392) |
e, como
 , temos
, temos
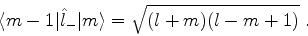 |
(393) |
Estes são os únicos elementos de matriz não-nulos, de
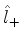 e
e 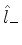 . A partir deles, podemos construir
os elementos de matriz de
. A partir deles, podemos construir
os elementos de matriz de  e
e 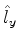 , pois
, pois
De fato,
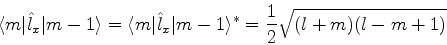 |
(397) |
Assim, os elementos de matriz de  que não são nulos são
que não são nulos são
 |
(398) |
Por um cálculo análogo obtêm-se os elementos de matriz não-nulos de 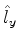 :
:
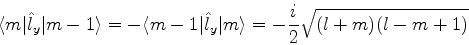 |
(399) |
Usando as expressões obtidas para os elementos de matriz, vamos construir as matrizes que
representam os operadores  ,
, 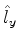 e
e 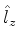 . Para este último, temos que
os elementos de matriz não-nulos são:
. Para este último, temos que
os elementos de matriz não-nulos são:
Os valores possíveis de  sendo +1/2 e -1/2, as matrizes terão a forma genérica:
sendo +1/2 e -1/2, as matrizes terão a forma genérica:
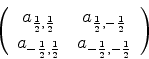 |
(402) |
onde
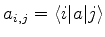 . Para
. Para 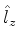 , portanto,
, portanto,
 |
(403) |
onde introduzimos a matriz
 |
(404) |
que é uma das matrizes de Pauli, que serão muito utilizadas no que segue.
Verifica-se facilmente que
onde introduzimos a matriz de Pauli 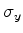 ,
,
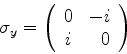 |
(408) |
Por um cálculo análogo chega-se a
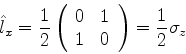 |
(409) |
Temos, portanto,
 |
(410) |
para 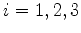 , sendo
, sendo
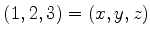 , como de costume. As matrizes de Pauli
são
, como de costume. As matrizes de Pauli
são
Representações matriciais de operadores são sempre em relação a uma
base. Qual é a base usada nas representações matriciais acima? Para descobri-la,
basta notar que a matriz que representa 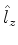 é diagonal. Logo, a base
é a dos autoestados de
é diagonal. Logo, a base
é a dos autoestados de 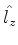 . Explicitamente, temos
. Explicitamente, temos
Desta relação vemos que os autoestados de 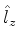 são representados pelas
matrizes coluna
são representados pelas
matrizes coluna
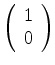 e
e
 , que formam uma base das matrizes
coluna
, que formam uma base das matrizes
coluna
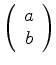 , com
, com 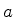 e
e 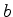 arbitrários.
Resta especificar o produto escalar de dois estados quaisquer, em termos de suas
representações matriciais. Verifica-se facilmente que o produto escalar de
arbitrários.
Resta especificar o produto escalar de dois estados quaisquer, em termos de suas
representações matriciais. Verifica-se facilmente que o produto escalar de
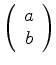 por
por
 é dado por
é dado por
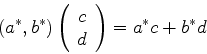 |
(416) |
De fato, em termos deste produto escalar, os elementos da base,
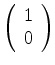 e
e
 são ortonormais,
o que prova a questão.
As matrizes
são ortonormais,
o que prova a questão.
As matrizes
têm propriedades especiais que facilitam o cálculo das
propriedades dos estados de spin 1/2.
P1:
 . (Imediata).
. (Imediata).
P2:
 são hermiteanas. (Imediata)
são hermiteanas. (Imediata)
P3:
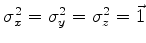 , onde
, onde
P4:
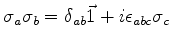 , cuja
demonstração é um exercício simples. Esta propriedade sintetiza a P3
e as seguintes relações:
, cuja
demonstração é um exercício simples. Esta propriedade sintetiza a P3
e as seguintes relações:
e assim por diante.
É conveniente introduzir a notação
que descreve as 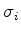 como componentes de um
``vetor'' denotado por
como componentes de um
``vetor'' denotado por 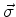 . Usando esta
convenção se escreve, por exemplo, se
. Usando esta
convenção se escreve, por exemplo, se 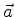 for
um vetor ordinário,
for
um vetor ordinário,
ou seja,
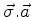 é uma matriz 2x2. Podemos então
enunciar a
é uma matriz 2x2. Podemos então
enunciar a
P5:
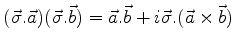 , onde
o termo entre parênteses é o produto vetorial ordinário.
Demonstração:
, onde
o termo entre parênteses é o produto vetorial ordinário.
Demonstração:
Teorema: Seja  uma matriz 2x2 complexa qualquer. Então existem
números
uma matriz 2x2 complexa qualquer. Então existem
números 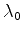 ,
,  ,
, 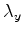 e
e 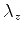 tais que
tais que
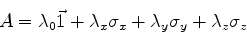 |
(424) |
Estes números são únicos. Ou seja,  ,
,  ,
,
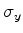 e
e 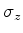 são uma base do espaço vetorial das
matrizes 2x2 complexas.
são uma base do espaço vetorial das
matrizes 2x2 complexas.
A demonstração consiste em exibir esses números. Suponhamos o problema
resolvido, isto é:
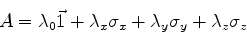 |
(425) |
Tomando o traço termo a termo, temos:
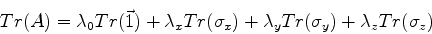 |
(426) |
onde usamos
 , para qualquer número
, para qualquer número  e qualquer matriz
e qualquer matriz  ,
temos, levando em conta a P1,
,
temos, levando em conta a P1,
 |
(427) |
ou
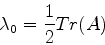 |
(428) |
Para calcular  procedemos assim: multiplicamos
(426) termo a termo, à esquerda, por
procedemos assim: multiplicamos
(426) termo a termo, à esquerda, por  ,
obtendo:
,
obtendo:
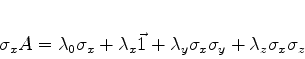 |
(429) |
Ora, os produtos
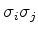 com
com 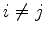 , são matrizes
de traço nulo. Logo, tomando, termo a termo, o traço de
(430), temos
, são matrizes
de traço nulo. Logo, tomando, termo a termo, o traço de
(430), temos
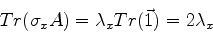 |
(430) |
Ou,
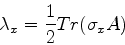 |
(431) |
e, procedendo analogamente,
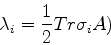 |
(432) |
Demonstra-se facilmente, usando este mtodo, que
 e as três matrizes de Pauli são linearmente independentes.
Além disso, o espaço vetorial das matrizes 2x2 complexas tem dimensão
4. Logo, o conjunto considerado é uma base, e portanto os coeficientes
calculados acima são únicos.
e as três matrizes de Pauli são linearmente independentes.
Além disso, o espaço vetorial das matrizes 2x2 complexas tem dimensão
4. Logo, o conjunto considerado é uma base, e portanto os coeficientes
calculados acima são únicos.
O problema que estudaremos aqui é o seguinte: uma
partícula de massa  e carga
e carga 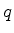 está sob ação de
um campo eletromagnético descrito por
está sob ação de
um campo eletromagnético descrito por 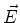 e
e  .
Determinar o Hamiltoniano da partícula.
.
Determinar o Hamiltoniano da partícula.
Não fosse pelo campo eletromagnético, o Hamiltoniano seria o de uma
partícula livre,
A força que age sobre uma partícula de carga 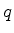 , devida aos campos
elétrico e magnético, é (força de Lorentz):
, devida aos campos
elétrico e magnético, é (força de Lorentz):
Em termos dos potenciais, temos,
Logo,
Como é bem sabido,22
Como
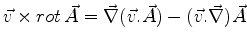 ,
temos
,
temos
ou seja,
![\begin{displaymath}
\vec{F}= q[-\vec{\nabla}(\phi - \frac{1}{c}\vec{v}.\vec{A})
-\frac{1}{c}\frac{d\vec{A}}{dt}] \;.
\end{displaymath}](img1321.png) |
(434) |
Seja
 . Vamos mostrar que a
lagrangeana
. Vamos mostrar que a
lagrangeana
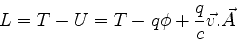 |
(435) |
descreve o movimento de uma partícula sob a ação da força
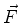 . Aqui, como de costume,
. Aqui, como de costume, 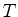 representa a energia cinética.
De fato,
representa a energia cinética.
De fato,
Logo, a equação de Lagrange,
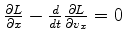 , dá
, dá
de modo que
Mas
de maneira que
Logo,
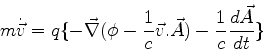 |
(436) |
Conclusão:
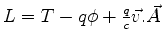 .
Passemos agora à construção do hamiltoniano.
.
Passemos agora à construção do hamiltoniano.
e, então,
Precisamos agora de uma propriedade importante das funções
homogêneas, o teorema de Euler (ver Apêndice):
Vamos usá-lo para calcular o Hamiltoniano 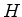 :
:
ou seja,
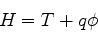 |
(438) |
Ora,
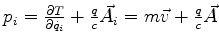 , pois
, pois
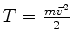 . Logo,
. Logo,
e, finalmente,
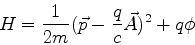 |
(439) |
Em palavras, no Hamiltoniano livre
substituo 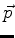 por
por
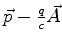 , e adiciono
, e adiciono  . Esta
é a chamada substituição mínima, ou acoplamento
mínimo. Se o hamiltoniano for mais geral, do tipo
. Esta
é a chamada substituição mínima, ou acoplamento
mínimo. Se o hamiltoniano for mais geral, do tipo
onde 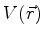 é a energia potencial, a mesma regra vale. Adicione-se
é a energia potencial, a mesma regra vale. Adicione-se
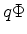 e substitua-se
e substitua-se 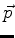 por
por
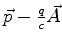 . Se houver
várias partículas, de momento s
. Se houver
várias partículas, de momento s 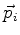 , faça-se a mesma
substituição para cada
, faça-se a mesma
substituição para cada 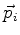 , adicionando-se termos
de energia potencial
, adicionando-se termos
de energia potencial 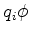 para cada partícula. Essas generalizações
são fáceis de demonstrar, seguindo exatamente o padrão do caso de uma
partícula livre.
para cada partícula. Essas generalizações
são fáceis de demonstrar, seguindo exatamente o padrão do caso de uma
partícula livre.
Uma função
 é dita homogênea de grau
é dita homogênea de grau 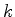 se
se
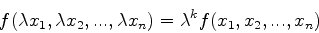 |
(440) |
Por exemplo, 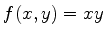 é homogênea de grau 2;
é homogênea de grau 2;
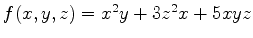 é homogênea de grau 3.
é homogênea de grau 3.
O teorema de Euler diz que, se 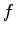 é uma função homogênea de grau
é uma função homogênea de grau
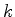 , então
, então
 |
(441) |
A demonstração é muito simples. Derive a Eq. 441 em relação
a  , e depois tome
, e depois tome 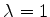 .
Seja
.
Seja
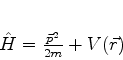 |
(442) |
o hamiltoniano de uma
partícula de spin 1/2 e carga 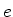 . Note-se que
. Note-se que
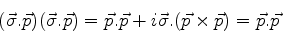 |
(443) |
de maneira que o hamiltoniano acima pode também ser escrito
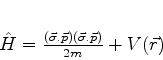 |
(444) |
O acoplamento mínimo, estudado no parágrafo anterior, consiste
na substituição de 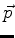 por
por
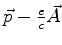 , onde
, onde
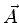 é o potencial vetor do campo eletromagnético que age sobre
a pertícula. Ora, se se realiza essa substituição em (443)
ou em (445), obtêm-se resultados diferentes. Verifica-se
que os resultados corretos são obtidos usando-se o hamiltoniano em
(445). Fica claro neste ponto, então, que o acoplamento
do spin com o campo eletromagnético que vamos introduzir tem um caráter
empírico. É só quando se utiliza a equação de Dirac para descrever
o spin do elétron que se obtém, diretamente da teoria e sem a necessidade
de fazer escolhas, um acoplamento definido (que corresponde àquele que,
aqui, foi escolhido por razões empíricas).
é o potencial vetor do campo eletromagnético que age sobre
a pertícula. Ora, se se realiza essa substituição em (443)
ou em (445), obtêm-se resultados diferentes. Verifica-se
que os resultados corretos são obtidos usando-se o hamiltoniano em
(445). Fica claro neste ponto, então, que o acoplamento
do spin com o campo eletromagnético que vamos introduzir tem um caráter
empírico. É só quando se utiliza a equação de Dirac para descrever
o spin do elétron que se obtém, diretamente da teoria e sem a necessidade
de fazer escolhas, um acoplamento definido (que corresponde àquele que,
aqui, foi escolhido por razões empíricas).
Devemos, então, descrever as interações eletromagnéticas da partícula
usando o hamiltoniano
![\begin{displaymath}
\hat{H}_{em}=\frac{1}{2m}\left\{\left[\vec{\sigma}.
\left(...
...}-\frac{e}{c}\vec{A}\right)\right]\right\}+V(\vec{r})
+e\phi
\end{displaymath}](img1368.png) |
(445) |
Como estamos interessados no campo magnético, vamos ignorar o último
termo. Consideremos o termo
![$\left[\vec{\sigma}.
\left(\vec{p}-\frac{e}{c}\vec{A}\right)\right].
\left[\vec{\sigma}.\left(\vec{p}-\frac{e}{c}\vec{A}\right)\right]$](img1369.png) . Temos
. Temos
Mas,
Escolhendo o gauge em que
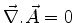 , temos
, temos
![\begin{displaymath}
\left[(\vec{p}.\vec{A})+(\vec{A}.\vec{p})\right]\psi =
-2i\hbar \vec{A}.\vec{\nabla}\psi
\end{displaymath}](img1380.png) |
(448) |
ou,
![\begin{displaymath}
\left[(\vec{p}.\vec{A})+(\vec{A}.\vec{p})\right]=2\vec{A}.\vec{p}
\end{displaymath}](img1381.png) |
(449) |
Temos ainda
Reunindo tudo, temos
 |
(451) |
O hamiltoniano  é obtido dividindo isso por
é obtido dividindo isso por 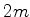 :
:
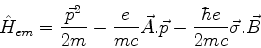 |
(452) |
Para o caso de um campo uniforme, temos
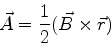 |
(453) |
como o leitor verificará facilmente. Resulta então que
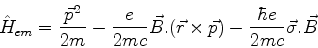 |
(454) |
Finalmente, usando
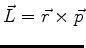 e
e
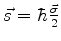 , temos
, temos
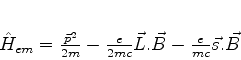 |
(455) |
Há ainda, é claro, o termo
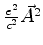 , que
omitimos porque, no tratamento perturbativo, representa uma correção
de ordem superior às que usualmente se calcula.
Henrique Fleming 2003
, que
omitimos porque, no tratamento perturbativo, representa uma correção
de ordem superior às que usualmente se calcula.
Henrique Fleming 2003
 concluímos que existe um valor máximo para o autovalor de
concluímos que existe um valor máximo para o autovalor de
![]() . Seja
. Seja ![]() este valor máximo, e
este valor máximo, e ![]() a autofunção
comum a
a autofunção
comum a
![]() e
e ![]() correspondente. Temos
correspondente. Temos
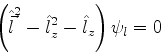
![$[\hat{\vec{l}}^2,\hat{l}_{-}]=0$](img1185.png) , segue que
, segue que

![]() o mínimo valor de
o mínimo valor de ![]() . Então
. Então
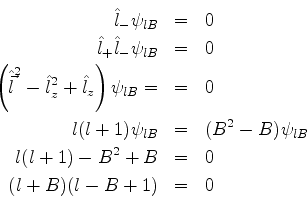
![]() , um pion em repouso tem momento angular tal que
, um pion em repouso tem momento angular tal que
![]() , e há mesons, ditos vetoriais, com momento angular em
repouso tal que
, e há mesons, ditos vetoriais, com momento angular em
repouso tal que ![]() . É costume, por abuso de linguagem, dizer
que essas partículas têm spin
. É costume, por abuso de linguagem, dizer
que essas partículas têm spin ![]() , spin
, spin ![]() , spin
, spin ![]() , etc.
, etc.
![]() ,
,
![]() e
e
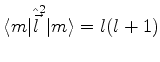 . Logo,
. Logo,
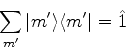
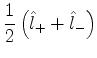
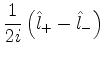
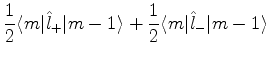

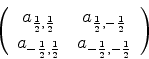


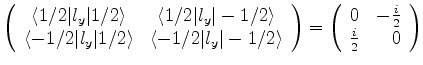
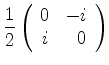
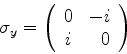
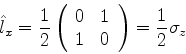
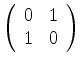

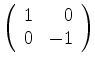
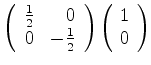
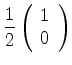
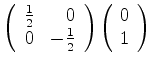

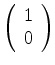 e
e
 , que formam uma base das matrizes
coluna
, que formam uma base das matrizes
coluna
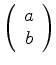 , com
, com 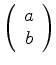 por
por
 é dado por
é dado por
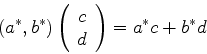
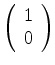 e
e
 são ortonormais,
o que prova a questão.
são ortonormais,
o que prova a questão.
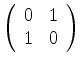

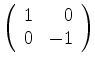
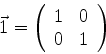
![]() e as três matrizes de Pauli são linearmente independentes.
Além disso, o espaço vetorial das matrizes 2x2 complexas tem dimensão
4. Logo, o conjunto considerado é uma base, e portanto os coeficientes
calculados acima são únicos.
e as três matrizes de Pauli são linearmente independentes.
Além disso, o espaço vetorial das matrizes 2x2 complexas tem dimensão
4. Logo, o conjunto considerado é uma base, e portanto os coeficientes
calculados acima são únicos.
![]() e carga
e carga ![]() está sob ação de
um campo eletromagnético descrito por
está sob ação de
um campo eletromagnético descrito por ![]() e
e ![]() .
Determinar o Hamiltoniano da partícula.
.
Determinar o Hamiltoniano da partícula.
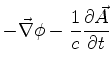
![\begin{displaymath}
\vec{F}=q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{\partial\vec{A}}
{\partial t}-\vec{v}\times rot \vec{A}]\}
\end{displaymath}](img1313.png)
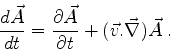
![$\displaystyle q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{d\vec{A}}{dt}
-(\vec{v}....
...\nabla})\vec{A}-\vec{\nabla}(\vec{v}.\vec{A})
+(\vec{v}.\vec{\nabla})\vec{A}]\}$](img1319.png)
![$\displaystyle q\{-\vec{\nabla}\phi - \frac{1}{c}[\frac{d\vec{A}}{dt}-
\vec{\nabla}(\vec{v}.\vec{A})]\}$](img1320.png)
![\begin{displaymath}
\vec{F}= q[-\vec{\nabla}(\phi - \frac{1}{c}\vec{v}.\vec{A})
-\frac{1}{c}\frac{d\vec{A}}{dt}] \;.
\end{displaymath}](img1321.png)
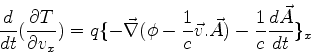
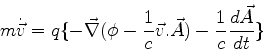
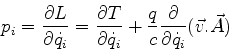
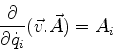

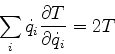
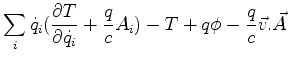
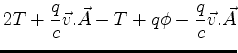
![]() é dita homogênea de grau
é dita homogênea de grau ![]() se
se
![]() é uma função homogênea de grau
é uma função homogênea de grau
![]() , então
, então

![$\displaystyle \left[\vec{\sigma}.\left(\vec{p}-\frac{e}{c}\vec{A}\right)\right].
\left[\vec{\sigma}.\left(\vec{p}-\frac{e}{c}\vec{A}\right)\right]=$](img1370.png)