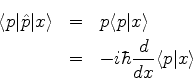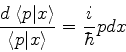Neste nosso tratamento elementar de mecânica quântica, consideraremos
o simbolismo introduzido por Dirac, que tem um significado matemático
não-trivial, como uma notação. Para fazer total justiça ao método, o leitor
faria bem em consultar a obra original de Dirac [1] . Para uma apresentação
mais adaptada à linguagem matemática contemporânea, veja [2].
Um vetor do espaço dos estados é descrito por um símbolo  ,
que se pronuncia ket . Um elemento do dual desse espaço é denotado
por
,
que se pronuncia ket . Um elemento do dual desse espaço é denotado
por 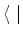 , e denominado
, e denominado 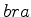 . O produto escalar dos estados
. O produto escalar dos estados
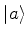 e
e 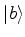 é denotado por
é denotado por
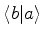 , e se trata
de um bra(c)ket , justificando os nomes.
, e se trata
de um bra(c)ket , justificando os nomes.
Seja  um operador. Denotaremos por
um operador. Denotaremos por  seus autoestados, de modo
que
seus autoestados, de modo
que
onde os números 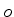 são os autovalores .
são os autovalores .
Os autoestados do operador de posição
são denotados por
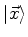 . O símbolo
. O símbolo
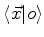 descreve o estado
descreve o estado  na representação das coordenadas:
na representação das coordenadas:
Alguns exemplos:
Seja uma base do espaço dos estados formada pelos kets
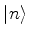 ,
,
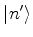 ,
,
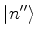 , etc. e
seja
, etc. e
seja  um operador. Então, os elementos de matriz de
um operador. Então, os elementos de matriz de  nessa base serão os números complexos
nessa base serão os números complexos
Note-se que:
Muito importante na notação de Dirac é uma classe de operadores que se
escrevem assim:
e são definidos pela sua ação sobre um kets arbitrário  :
:
Sejam 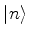 autoestados de um operador hermiteano. Então, a relação
de completude se escreve
autoestados de um operador hermiteano. Então, a relação
de completude se escreve
Quando o espectro é contínuo, por exemplo, no caso do operador de posição,
a soma é substituída por uma integral:
O principal uso dessas representações do operador 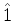 é o seguinte:
seja
é o seguinte:
seja
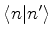 um produto escalar. Então,
um produto escalar. Então,
e, como
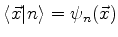 ,
,
mostrando que efetivamente se trata do produto escalar anteriormente introduzido.
Considere os operadores 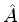 e
e  e o seu produto,
e o seu produto,
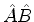 .
Seja
.
Seja 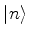 uma base. Os elementos de matriz do operador produto nessa base
são
uma base. Os elementos de matriz do operador produto nessa base
são
que exibe a expressão correta para o produto clássico de matrizes.
Seja 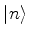 um estado qualquer. Sua função de onda na representação das coordenadas é,
como vimos,
um estado qualquer. Sua função de onda na representação das coordenadas é,
como vimos,
Sejam
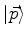 os autoestados do momento , e
os autoestados do momento , e
sua relação de completude. Então, a função de onda de 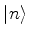 na representação
do momento é
na representação
do momento é
que pode ser escrita
Daqui, por comparação com um resultado anterior pode-se inferir que
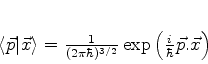 |
(382) |
Henrique Fleming 2003
![]() ,
que se pronuncia ket . Um elemento do dual desse espaço é denotado
por
,
que se pronuncia ket . Um elemento do dual desse espaço é denotado
por ![]() , e denominado
, e denominado ![]() . O produto escalar dos estados
. O produto escalar dos estados
![]() e
e ![]() é denotado por
é denotado por
![]() , e se trata
de um bra(c)ket , justificando os nomes.
, e se trata
de um bra(c)ket , justificando os nomes.
![]() um operador. Denotaremos por
um operador. Denotaremos por ![]() seus autoestados, de modo
que
seus autoestados, de modo
que
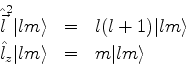
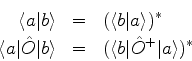
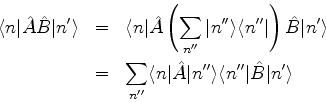
![]() um estado qualquer. Sua função de onda na representação das coordenadas é,
como vimos,
um estado qualquer. Sua função de onda na representação das coordenadas é,
como vimos,