Subsections
O átomo de Hidrogênio
O núcleo do átomo de hidrogênio é cerca de 2000 vezes mais pesado
do que um elétron. Por isso se pode ignorar o movimento do núcleo
e descrever o átomo simplesmente como um elétron movendo-se com
energia potencial
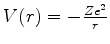 . A Eq.(335) é
então escrita
. A Eq.(335) é
então escrita
![\begin{displaymath}
-\frac{\hbar^2}{2m}\frac{d^2u}{dr^2}+\left[\frac{\hbar^2 l(l+1)} {
2mr^2} -\frac{Ze^2}{r}\right]u(r)=Eu(r)
\end{displaymath}](img985.png) |
(336) |
Note-se que esta equação descreve mais do que o átomo de
hidrogênio: a interação de um elétron com um campo coulombiano
possui também casos em que o elétron não permanece nas
proximidades do núcleo, mas afasta-se indefinidamente dele:
trata-se do espalhamento de um elétron por um campo coulombiano.
Aqui vamos estudar apenas os estados ligados do
elétron: aqueles em que ele está preso ao núcleo, formando um
átomo. O que caracteriza esses estados, na Eq.(336), é
que eles possuem energia negativa. Portanto,
estudaremos as soluções do problema de autovalores dado pela
Eq.(336), com  , e, portanto,
, e, portanto, 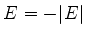 .
.
É conveniente introduzir variáveis adimensionais. Substituiremos
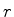 por
por
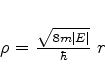 |
(337) |
e a energia , ou, antes, o seu inverso, por
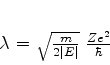 |
(338) |
Deixamos ao leitor a tarefa de verificar que, efetivamente, 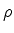 e
e 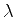 são quantidades adimensionais. Verifica-se facilmente
que
são quantidades adimensionais. Verifica-se facilmente
que
e que a Eq.(336) pode ser reescrita como
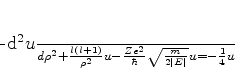 |
(339) |
ou, finalmente,
![\begin{displaymath}
\frac{d^2 u}{d\rho ^2}-\frac{l(l+1)}{\rho ^2}u +
\left[\frac{\lambda}{\rho}-\frac{1}{4}\right]u=0
\end{displaymath}](img991.png) |
(340) |
Resolver este problema de autovalores consiste em determinar os
pares 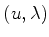 submetidos à condição de que
submetidos à condição de que
que corresponde ao fato de que o átomo tem dimensões finitas.
Para resolver este problema utilizaremos uma técnica devida a
Sommerfeld. Em primeiro lugar, estudaremos que tipos de
comportamento assintótico, para 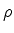 grande, as soluções de
Eq.(340) podem ter. Note-se que a equação
grande, as soluções de
Eq.(340) podem ter. Note-se que a equação
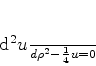 |
(341) |
coincide com a Eq.(340) para grandes valores de 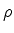 .
Podemos, portanto, afirmar que as soluções de Eq.(341)
devem coincidir com o limite, para grandes
.
Podemos, portanto, afirmar que as soluções de Eq.(341)
devem coincidir com o limite, para grandes 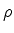 , das soluções da
Eq.(340).
Considere a equação
, das soluções da
Eq.(340).
Considere a equação
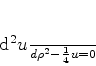 |
(342) |
e vamos multiplicar cada um de seus termos por
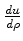 ,
obtendo
,
obtendo
O leitor verificará facilmente que esta equação é a mesma que
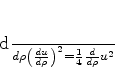 |
(343) |
ou
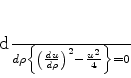 |
(344) |
Portanto,
onde 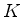 é uma constante. Mas tanto
é uma constante. Mas tanto 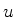 quanto as suas derivadas
tendem a zero no infinito. Logo, a constante
quanto as suas derivadas
tendem a zero no infinito. Logo, a constante 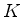 deve ser nula,
pois, calculada no infinito é nula, e tem o mesmo valor em todos
os pontos. Conseqüentemente,
deve ser nula,
pois, calculada no infinito é nula, e tem o mesmo valor em todos
os pontos. Conseqüentemente,
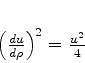 |
(345) |
e
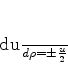 |
(346) |
As soluções dessas equações são
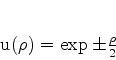 |
(347) |
das quais a que satisfaz os requisitos físicos de se anular no
infinito é
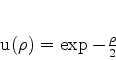 |
(348) |
Este é, então, o comportamento assintótico que as soluções da
Eq.(340) devem ter.
Vamos então procurar soluções da Eq.(340) da forma
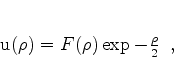 |
(349) |
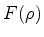 sendo um polinômio em
sendo um polinômio em 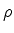 . A razão de ser um
polinômio é que o comportamento assintótico de (349)
deve ainda ser dado pelo termo exponencial, o que é garantido se
. A razão de ser um
polinômio é que o comportamento assintótico de (349)
deve ainda ser dado pelo termo exponencial, o que é garantido se
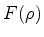 for um polinômio. Uma análise mais fina mostraria que,
se se admitisse que
for um polinômio. Uma análise mais fina mostraria que,
se se admitisse que 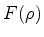 fosse uma série infinita, sua soma
seria essencialmente uma exponencial em
fosse uma série infinita, sua soma
seria essencialmente uma exponencial em 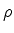 , alterando o
comportamento assintótico.20
, alterando o
comportamento assintótico.20
Seja 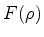 uma expressão da forma
uma expressão da forma
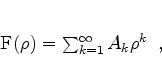 |
(350) |
onde a potência mais baixa é a primeira para assegurar que
Derivando termo a termo, temos
Inserindo estas expressões na Eq.(350), temos
![\begin{displaymath}
\sum_{k=1}^{\infty}\left\{k(k-1)A_{k}\rho ^{k-2}-kA_{k}\rh...
...}{\rho}-\frac{l(l+1)}{\rho
^2}\right]A_{k}\rho^{k}\right\}=0
\end{displaymath}](img1010.png) |
(351) |
O coeficiente da potência 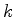 de
de 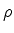 é dado por
é dado por
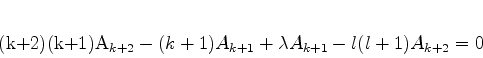 |
(352) |
para que a equação diferencial seja satisfeita termo a termo.
Diminuindo o valorde 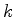 de uma unidade, temos uma relação mais
conveniente:
de uma unidade, temos uma relação mais
conveniente:
![\begin{displaymath}
A_{k+1}\left[(k+1)k-l(l+1)\right] = (k-\lambda) A_k
\end{displaymath}](img1012.png) |
(353) |
ou, equivalentemente,
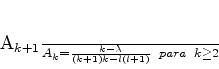 |
(354) |
Para os índices mais baixos temos as equações
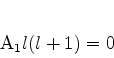 |
(355) |
![\begin{displaymath}
\left[2-l(l+1)\right]A_2 + (\lambda -1)A_1 =0
\end{displaymath}](img1015.png) |
(356) |
A equação (354) é muito importante. Dela vemos que, para
que a série se interrompa em algum ponto, tornando-se um
polinômio, devemos ter que 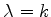 . Ora, os
. Ora, os 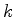 são
inteiros, logo, a condição para que a série se interrompa é que
exista um inteiro
são
inteiros, logo, a condição para que a série se interrompa é que
exista um inteiro 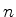 tal que
tal que
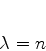 |
(357) |
Como
temos
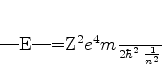 |
(358) |
ou, eqüivalentemente,
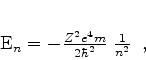 |
(359) |
que é a fórmula de Bohr! Voltando ao cálculo das autofunções, além
da condição 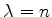 , devemos ter que
, devemos ter que
 , de
outra forma, na equação (354), o denominador se anularia
ao mesmo tempo que o numerador, não garantindo o anulamento do
coeficiente
, de
outra forma, na equação (354), o denominador se anularia
ao mesmo tempo que o numerador, não garantindo o anulamento do
coeficiente 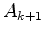 . Portanto devemos ter
. Portanto devemos ter 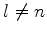 .
.
Vamos construir as primeiras soluções. Tomemos
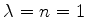 A
este valor corresponde a energia
A
este valor corresponde a energia
que é a energia do estado fundamental do átomo de
hidrogênio (o de energia mais baixa). Para este valor de 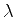 podemos ter
podemos ter 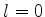 , mas não
, mas não 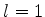 . Então, das equações
. Então, das equações
temos Que 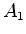 é indeterminado, e
é indeterminado, e 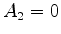 , assim como os
coeficientes de índice mais alto. Temos então, para a solução,
, assim como os
coeficientes de índice mais alto. Temos então, para a solução,
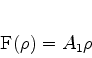 |
(360) |
e
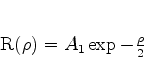 |
(361) |
Em termos de 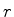 , usando
, usando
e introduzindo
denominado raio de Bohr, obtemos, após cálculos simples,
Para o estado fundamental, temos, então,
 |
(362) |
que é também a função completa, pois 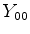 é constante.
é constante.
Para
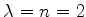 temos as possibilidades
temos as possibilidades 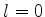 e
e 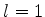 . Para
o primeiro caso, temos, novamente,
. Para
o primeiro caso, temos, novamente, 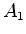 indeterminado. Para
indeterminado. Para
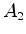 , usamos a equação (353), que dá
, usamos a equação (353), que dá
ou seja,
A solução então é
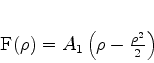 |
(363) |
e
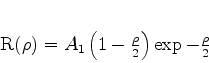 |
(364) |
Expressando em termos de 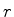 , obtemos
, obtemos
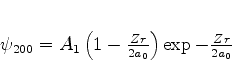 |
(365) |
onde usamos a notação tradicional para os autoestados do átomo de
hidrogênio:
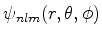 . O leitor, neste ponto,
deveria ser capaz de mostrar que
. O leitor, neste ponto,
deveria ser capaz de mostrar que
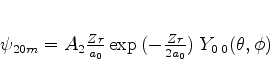 |
(366) |
No segundo caso, 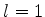 ,vemos, da Eq.(355), que
,vemos, da Eq.(355), que
enquanto 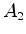 é indeterminado.
é indeterminado. 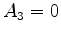 , assim como os índices
mais altos. Logo,
, assim como os índices
mais altos. Logo,
A expressão em termos de 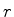 vem a ser
vem a ser
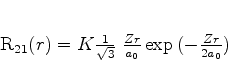 |
(367) |
Como vimos, a função radial fica definida quando se dão os valores
de 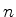 e
e 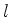 . Por isso ela é denotada por
. Por isso ela é denotada por 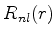 . Para o caso
de
. Para o caso
de 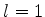 a dependência angular não é trivial, pois temos
a dependência angular não é trivial, pois temos
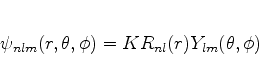 |
(368) |
que, nesse caso dá
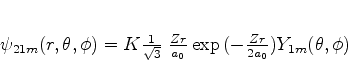 |
(369) |
com 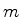 podendo tomar os valores 1, 0, e -1.
podendo tomar os valores 1, 0, e -1.
Note que a energia fica totalmente determinada por 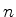 . Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com
. Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com 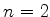 . Podemos ter
. Podemos ter 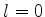 , que dá um único
estado, ou
, que dá um único
estado, ou 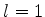 , que admite 3 valores de
, que admite 3 valores de 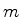 . No total, então, há
4 estados neste nível de energia . Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível
. No total, então, há
4 estados neste nível de energia . Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível 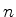 é
é  . O numero quântico
. O numero quântico 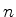 é denominado
número quântico principal.
é denominado
número quântico principal.
A seguir apresentamos uma lista das partes radiais de algumas
funções de onda do átomo de hidrogênio.
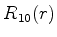 |
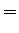 |
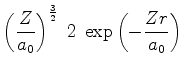 |
(370) |
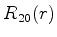 |
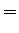 |
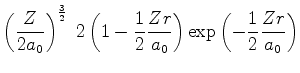 |
(371) |
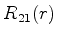 |
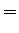 |
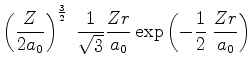 |
(372) |
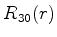 |
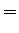 |
![$\displaystyle \left(\frac{Z}{3a_0}\right)^{\frac{3}{2}}\;2\left[1-\frac{2}{3}\f...
...(\frac{Zr}{a_0}\right)^2\right]
\exp{\left(-\frac{1}{3}\;\frac{Zr}{a_0}\right)}$](img1062.png) |
(373) |
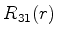 |
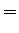 |
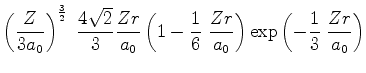 |
(374) |
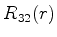 |
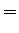 |
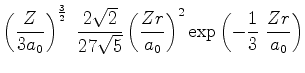 |
(375) |
Até agora escrevemos as funções de onda assim:
Como determinar a constante 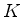 ? Uma vez que os harmônicos
esféricos são normalizados por conta própria, pois
? Uma vez que os harmônicos
esféricos são normalizados por conta própria, pois
devemos ter
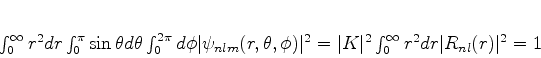 |
(376) |
Exemplo: para o estado 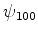 ,
,
Usando
obtemos
confirmando o valor da tabela.
De posse da expressão detalhada da função de onda, podemos fazer
perguntas interessantes. Qual é a probabilidade de o elétron
estar, no estado fundamental do átomo de hidrogênio, entre 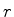 e
e
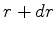 ? Ela é dada por
? Ela é dada por
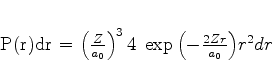 |
(377) |
Para que valor de 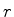 a probabilidade é máxima (para idênticos
a probabilidade é máxima (para idênticos
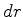 )? No ponto de máximo, teremos
)? No ponto de máximo, teremos
ou
Logo, para o átomo de hidrogênio (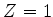 ), temos que a
probabilidade máxima é para
), temos que a
probabilidade máxima é para 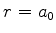 , o raio de
Bohr!21
, o raio de
Bohr!21
Vamos calcular agora a velocidade média do elétron no estado
fundamental.
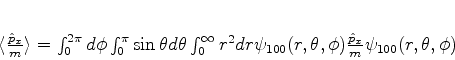 |
(378) |
Usando
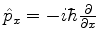 e
e
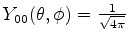 , obtemos
, obtemos
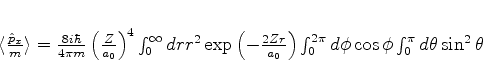 |
(379) |
onde usamos
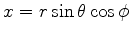 . Como
. Como
temos que o valor médio da componente 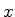 da velocidade do elétron
no estado fundamental é 0. Como o estado é esfericamente
simétrico, o mesmo resultado deve valer para as outras
componentes. Logo,
da velocidade do elétron
no estado fundamental é 0. Como o estado é esfericamente
simétrico, o mesmo resultado deve valer para as outras
componentes. Logo,
Isto posto, podemos dizer que e elétron está em repouso, no estado
fundamental? Certamente não! Em qualquer modêlo clássico com
órbita circular (qualquer órbita fechada, de fato) o elétron está
em movimento e sua velocidade média é zero. Para obter mais
informações sobre o que o elétron faz no estado fundamental do
átomo de hidrogênio, vamos calcular sua energia
cinética média. Ela é dada por:
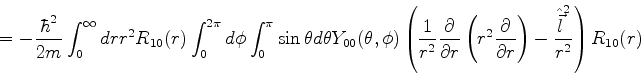 |
(380) |
Usando as integrais
e
obtemos o resultado, para 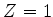 ,
,
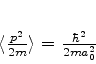 |
(381) |
Logo, o elétron não está parado. E nem poderia: se tivesse momento
perfeitamente definido (no caso, nulo), sua posição teria de ser
totalmente indefinida, pelo princípio da
incerteza. Como a
incerteza na posição é da ordem de 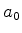 e, da
Eq.(382), vemos que a incerteza no momento é da ordem
de
e, da
Eq.(382), vemos que a incerteza no momento é da ordem
de
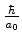 , vemos que o produto das incerteza é da
ordem de
, vemos que o produto das incerteza é da
ordem de 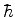 . Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!
. Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!
1. Os estados estacionários do átomo de Hidrogênio são denotados
por
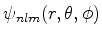 . A seguinte superposição:
. A seguinte superposição:
com 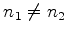 ,
, 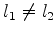 ,
, 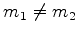 , é um estado do Hidrogênio,
que não é um estado estacionário, e não é autofunção nem de
, é um estado do Hidrogênio,
que não é um estado estacionário, e não é autofunção nem de
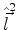 nem de
nem de 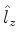 . Dentro deste estilo, construa
. Dentro deste estilo, construa
(a) Um estado do Hidrogênio que seja autofunção simultanea de 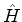 e
e
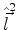 , mas
não de
, mas
não de 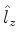 .
.
(b) Um estado do Hidrogênio que seja autofunção simultânea de 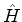 e
e 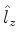 , mas
não de
, mas
não de
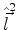 .
.
2. Uma partícula livre executa movimento unidimensional ao longo do eixo 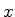 ,
e sua função de onda em
,
e sua função de onda em 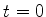 é
é
onde 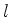 é uma constante real. Determine
é uma constante real. Determine 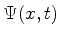 .
.
3.(a) Um sistema físico é descrito por um hamiltoniano
onde  é hermiteano. Mostre que
é hermiteano. Mostre que 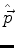 é hermiteano,
e que se um operador é hermiteano, seu quadrado também é. Finalmente, mostre
que os autovalores da energia do sistema são positivos ou nulos.
é hermiteano,
e que se um operador é hermiteano, seu quadrado também é. Finalmente, mostre
que os autovalores da energia do sistema são positivos ou nulos.
(b) É possível um operador ser ao mesmo tempo unitário e hermiteano? Exemplo!
(c) Demonstre que
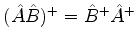 .
.
(d) Demonstre que, se 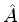 e
e  são hermiteanos,
são hermiteanos,
![$\frac{1}{i}[\hat{A},\hat{B}]$](img1103.png) também é.
também é.
(e) Sejam
 e
e
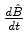 nulos. Mostre que
nulos. Mostre que
![$\frac{d}{dt}[\hat{O}, \hat{B}] = \hat{0}$](img1106.png) , onde
, onde 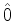 , o operador ``zero'',
é tal que, qualquer que seja a função de onda
, o operador ``zero'',
é tal que, qualquer que seja a função de onda 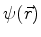 ,
,
Sugestão: identidade de Jacobi.
4.(a) Determine
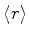 e
e
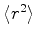 para o elétron no estado fundamental do átomo de
hidrogênio. Expresse suas respostas em termos do raio de Bohr
para o elétron no estado fundamental do átomo de
hidrogênio. Expresse suas respostas em termos do raio de Bohr
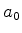 . Determine também
. Determine também 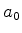 , que é o raio da ``órbita de
Bohr'' do
estado de mais baixa energia , no modelo de Bohr.
, que é o raio da ``órbita de
Bohr'' do
estado de mais baixa energia , no modelo de Bohr.
(b)Determine
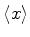 e
e
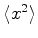 no estado
fundamental sem calcular mais integrais, usando o resultado
anterior e as simetrias do estado fundamental.
no estado
fundamental sem calcular mais integrais, usando o resultado
anterior e as simetrias do estado fundamental.
(c) Determine
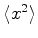 no estado
no estado
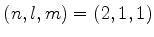 .
Note que este estado não é simétrico em
.
Note que este estado não é simétrico em 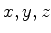 .
.
5. Qual é a probabilidade 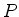 de que um elétron no
estado fundamental do átomo de hidrogênio seja encontrado
dentro do
núcleo?
de que um elétron no
estado fundamental do átomo de hidrogênio seja encontrado
dentro do
núcleo?
(a)Primeiro calcule a resposta exata. Denote o raio do
núcleo por 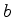 .
.
(b) Expanda o seu resultado como uma série de potências no número
pequeno
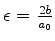 , e mostre que o termo de ordem
mais baixa é cúbico:
, e mostre que o termo de ordem
mais baixa é cúbico:
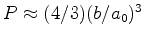 . Este termo
deveria
já ser uma boa aproximação, pois
. Este termo
deveria
já ser uma boa aproximação, pois 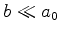 .
.
(c) Alternativamente, poderíamos pensar que a função de onda do
elétron é essencialmente constante sobre o pequeno volume do
núcleo, de modo que
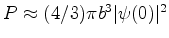 .
Verifique que o resultado é efetivamente bom.
.
Verifique que o resultado é efetivamente bom.
(d) Use
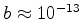 cm e
cm e
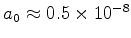 cm para uma estimativa numérica de
cm para uma estimativa numérica de 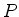 . Grosso modo,
isto representa a fração do tempo em que o elétron se encontra
dentro do núcleo.
. Grosso modo,
isto representa a fração do tempo em que o elétron se encontra
dentro do núcleo.
6. Estime, a partir do princípio de incerteza, quanto
tempo um lápis pode ficar em equilíbrio vertical sobre a sua
ponta.
7. Uma bola perfeitamente elástica, localizada entre
duas paredes paralelas, move-se perpendicularmente a elas, sendo
refletida de uma para outra. Perfeitamente elástica quer dizer que
a energia cinética não se altera.. Usando a mecânica clássica,
calcule a variação da energia da bola se as paredes passam a se
aproximar, lenta e uniformemente, uma da outra. Mostre que esta
variação de energia é exatamente o que se obtém na mecânica
quântica se o número quântico principal 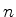 da bola permanece
constante.
Henrique Fleming 2003
da bola permanece
constante.
Henrique Fleming 2003
![]() , e, portanto,
, e, portanto, ![]() .
.
![]() por
por
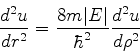
![]() grande, as soluções de
Eq.(340) podem ter. Note-se que a equação
grande, as soluções de
Eq.(340) podem ter. Note-se que a equação
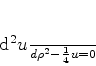
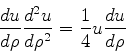
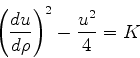
![]() uma expressão da forma
uma expressão da forma
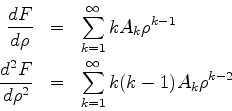
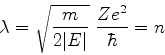
![]() A
este valor corresponde a energia
A
este valor corresponde a energia
![\begin{eqnarray*}
A_1 l(l+1) & = & 0\\
\left[2 - l(l+1)\right]A_2 = (\lambda -1)A_1
\end{eqnarray*}](img1029.png)
![]() , usando
, usando
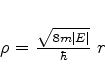
![]() temos as possibilidades
temos as possibilidades ![]() e
e ![]() . Para
o primeiro caso, temos, novamente,
. Para
o primeiro caso, temos, novamente, ![]() indeterminado. Para
indeterminado. Para
![]() , usamos a equação (353), que dá
, usamos a equação (353), que dá
![]() . Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com
. Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com ![]() . Podemos ter
. Podemos ter ![]() , que dá um único
estado, ou
, que dá um único
estado, ou ![]() , que admite 3 valores de
, que admite 3 valores de ![]() . No total, então, há
4 estados neste nível de energia . Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível
. No total, então, há
4 estados neste nível de energia . Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível ![]() é
é ![]() . O numero quântico
. O numero quântico ![]() é denominado
número quântico principal.
é denominado
número quântico principal.
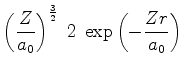
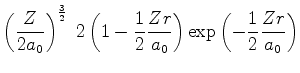
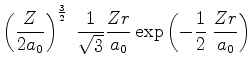
![$\displaystyle \left(\frac{Z}{3a_0}\right)^{\frac{3}{2}}\;2\left[1-\frac{2}{3}\f...
...(\frac{Zr}{a_0}\right)^2\right]
\exp{\left(-\frac{1}{3}\;\frac{Zr}{a_0}\right)}$](img1062.png)
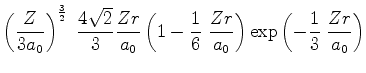
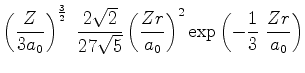
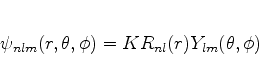
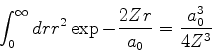
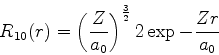
![]() e
e
![]() ? Ela é dada por
? Ela é dada por
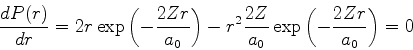
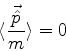
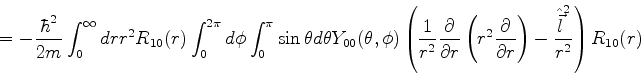
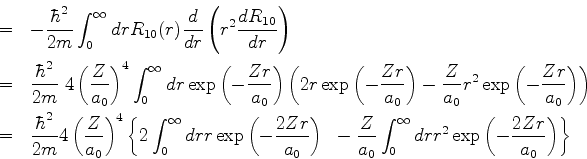
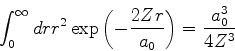
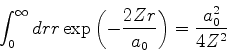
![]() e, da
Eq.(382), vemos que a incerteza no momento é da ordem
de
e, da
Eq.(382), vemos que a incerteza no momento é da ordem
de
![]() , vemos que o produto das incerteza é da
ordem de
, vemos que o produto das incerteza é da
ordem de ![]() . Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!
. Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!
![]() ,
e sua função de onda em
,
e sua função de onda em ![]() é
é