Potenciais com simetria central
Chamam-se assim os potenciais que, expressos em coordenadas
esféricas, são funções apenas da variável radial 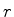 . O caso mais
importante, naturalmente, é o do átomo de Hidrogênio. Vamos tratar
primeiramente o caso geral.
. O caso mais
importante, naturalmente, é o do átomo de Hidrogênio. Vamos tratar
primeiramente o caso geral.
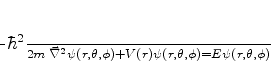 |
(330) |
é a equação de Schrödinger para estados estacionários de uma
partícula de massa 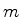 cuja energia potencial depende apenas da
distância à origem. Utilizando coordenadas esféricas, temos
cuja energia potencial depende apenas da
distância à origem. Utilizando coordenadas esféricas, temos
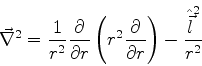 |
(331) |
onde
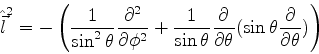 |
(332) |
é o operador de momento angular total (veja Eq.(294) e
anteriores).
Vamos procurar soluções da Eq.(331) que sejam da forma
Como
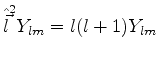 , tem-se
, tem-se
| |
|
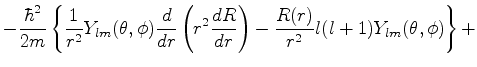 |
|
| |
|
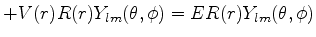 |
(333) |
Cancelando 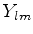 ,
,
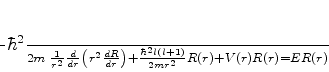 |
(334) |
Introduzimos agora a função
satisfazendo 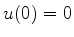 . Reescrevendo a Eq.(334) em
termos de
. Reescrevendo a Eq.(334) em
termos de 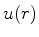 , obtém-se
, obtém-se
![\begin{displaymath}
-\frac{\hbar^2}{2m}\frac{d^2u}{dr^2}+\left[\frac{\hbar^2 l(l+1)} {
2mr^2} + V(r)\right]u(r)=Eu(r)
\end{displaymath}](img979.png) |
(335) |
Esta é a chamada equação radial de Schrödinger, e contém
toda a dinâmica. Lembrando a condição 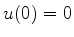 , decorrência de que
, decorrência de que
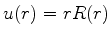 com
com 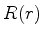 regular na origem (os casos interessantes
fisicamente não são aqueles em que a partícula tem probabilidade
zero de estar em qualquer lugar que não a origem!), podemos
interpretar a equação acima como uma equação de Schrödinger de um
movimento unidimensional sujeito aos seguintes ``potenciais'':(a)
Uma parede impenetrável em
regular na origem (os casos interessantes
fisicamente não são aqueles em que a partícula tem probabilidade
zero de estar em qualquer lugar que não a origem!), podemos
interpretar a equação acima como uma equação de Schrödinger de um
movimento unidimensional sujeito aos seguintes ``potenciais'':(a)
Uma parede impenetrável em 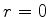 , que impede a passagem da
partícula para valores negativos de
, que impede a passagem da
partícula para valores negativos de 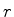 . (b) Um potencial do tipo
. (b) Um potencial do tipo
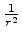 repulsivo, chamado de potencial centrífugo. (c) O
verdadeiro potencial,
repulsivo, chamado de potencial centrífugo. (c) O
verdadeiro potencial, 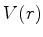 .
.
O potencial centrífugo vem do fato
de que a eliminação das variáveis 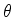 e
e 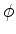 , é formalmente
eqüivalente a colocar-se em um sistema de referência que ``gira''
com o sistema físico, ou seja, em um sistema não-inercial. Surgem,
então, as chamadas forças de inércia, das quais a
força centrífuga é a mais popular.19
Henrique Fleming 2003
, é formalmente
eqüivalente a colocar-se em um sistema de referência que ``gira''
com o sistema físico, ou seja, em um sistema não-inercial. Surgem,
então, as chamadas forças de inércia, das quais a
força centrífuga é a mais popular.19
Henrique Fleming 2003
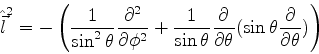
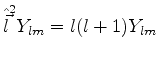 , tem-se
, tem-se