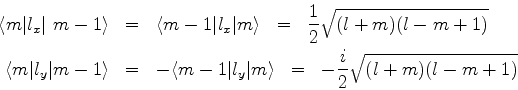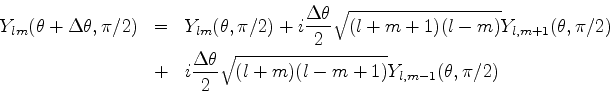Subsections
Autofunções do momento angular
Por razões técnicas é conveniente introduzir os operadores
não-hermiteanos
Seus principais comutadores são:
![\begin{displaymath}[\hat{\vec{l}}^2,\hat{l}_{\pm}]=0
\end{displaymath}](img833.png) |
(281) |
![\begin{displaymath}[\hat{l}_z,\hat{l}_+]=\hat{l}_+
\end{displaymath}](img834.png) |
(282) |
![\begin{displaymath}[\hat{l}_z,\hat{l}_{-}]=-\hat{l}_{-}
\end{displaymath}](img835.png) |
(283) |
todas fáceis de obter. Note-se ainda que
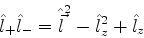 |
(284) |
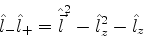 |
(285) |
As autofunções da componente z do momento angular
As autofunções de 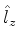 são funções
são funções  tais que
tais que
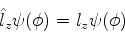 |
(286) |
onde 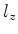 é um número. Omitimos aqui, por simplicidade, as outras
variáveis,
é um número. Omitimos aqui, por simplicidade, as outras
variáveis,  e
e  , de que a função
, de que a função  em geral depende
porque são irrelevantes para este problema. Como
em geral depende
porque são irrelevantes para este problema. Como
temos, para a Eq.(286),
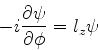 |
(287) |
cuja solução é
Devemos ainda ter
o que exige que
ou seja, que  seja um número inteiro. Vamos denotá-lo por
seja um número inteiro. Vamos denotá-lo por
 . Então,
. Então,
 |
(288) |
que é satisfeita para qualquer  inteiro,
inteiro,
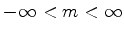 . Normalizando, temos
. Normalizando, temos
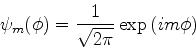 |
(289) |
Autofunções simultâneas do momento angular total e da
componente z
Seja  a autofunção de
a autofunção de 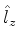 de
autovalor
de
autovalor  . Calculemos
. Calculemos
Logo, se
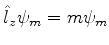 , então
, então
Analogamente se mostra que
Assim, usando os operadores 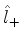 e
e 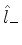 , pode-se
varrer todo o espectro do operador
, pode-se
varrer todo o espectro do operador 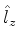 .
.
Considere o operador
Lema:Se 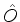 é hermiteano,
é hermiteano,
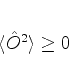 |
(290) |
para qualquer estado.
Demonstração:
Em particular, segue que
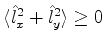 , logo,
, logo,
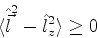 |
(291) |
A construção das autofunções de
 é facilitada pelo fato
de que a expressão de
é facilitada pelo fato
de que a expressão de
 é um operador diferencial familiar à
física clássica. De fato, um cálculo direto leva a
é um operador diferencial familiar à
física clássica. De fato, um cálculo direto leva a
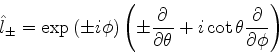 |
(292) |
e, como
obtém-se
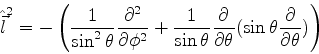 |
(293) |
Acontece que o laplaceano em coordenadas esféricas é
 |
(294) |
ou seja,
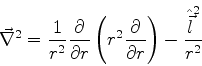 |
(295) |
Os físicos do século XIX resolveram o problema de determinar as autofunções de
 :18
essas funções são os harmônicos esféricos,
:18
essas funções são os harmônicos esféricos,
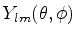 , que satisfazem as equações
de autovalores
, que satisfazem as equações
de autovalores
Os harmônicos esféricos são muito bem conhecidos. Para um estudo deles no contexto clássico
as minhas referências preferidas são Courant [6] e Sommerfeld [9]. Nessas notas,
usando técnicas que introduziremos a seguir, construiremos explicitamente os 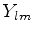 . Para o momento
é suficiente informar que
. Para o momento
é suficiente informar que
ou seja, é o produto de uma função de 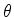 por uma autofunção de
por uma autofunção de 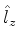 .
.
Uma observação importante: as autofunções de 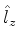 são as funções
são as funções
 para
qualquer inteiro
para
qualquer inteiro  . Quando construirmos as autofunções comuns a
. Quando construirmos as autofunções comuns a
 e
e 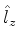 , veremos que
, veremos que  sofrerá mais restrições. De fato, como temos
sofrerá mais restrições. De fato, como temos
segue que
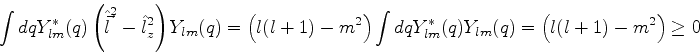 |
(298) |
Portanto, dado 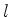 ,
,  não pode ser qualquer inteiro. O maior valor permitido
é tal que
não pode ser qualquer inteiro. O maior valor permitido
é tal que
Vê-se imediatamente que 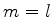 é permitido, mas
é permitido, mas  é proibido. Logo,
o máximo valor permitido de
é proibido. Logo,
o máximo valor permitido de  para as autofunções
para as autofunções 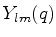 é
é
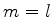 . Um argumento an'alogo mostra que o menor é
. Um argumento an'alogo mostra que o menor é 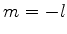 . Resumindo,
. Resumindo,
Neste intervalo,
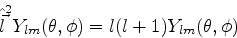 |
(299) |
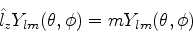 |
(300) |
Assim, para cada 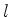 há
há  valores distintos de
valores distintos de  .
Chamaremos de operadores vetoriais operadores do tipo
.
Chamaremos de operadores vetoriais operadores do tipo
e que satisfazem as seguintes relações de comutação com as componentes do
momento angular:
![\begin{displaymath}[\hat{l}_a, \hat{T}_b]= i\epsilon_{abc}\hat{T}_c
\end{displaymath}](img885.png) |
(301) |
onde a costumeira convenção indica uma soma sobre os valores do índice 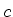 ,
e, sendo
,
e, sendo 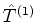 e
e 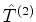 dois operadores desse tipo,
dois operadores desse tipo,
![\begin{displaymath}[\hat{l}_i, \hat{T}^{(1)}_{j}\hat{T}^{(2)}_{j}]=0
\end{displaymath}](img889.png) |
(302) |
Exemplos: 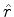 ,
, 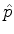 e
e 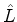 são, todos, operadores vetoriais.
são, todos, operadores vetoriais.
Das relações acima segue, em particular, que, para qualquer operador vetorial  ,
,
![\begin{displaymath}[\hat{l}_i,\hat{T}_j\hat{T}_j]=0
\end{displaymath}](img893.png) |
(303) |
Seja 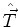 um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
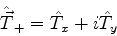 |
(304) |
Facilmente se verifica que
![\begin{displaymath}[\hat{l}_z,\hat{T}_{+}]=\hat{T}_{+}
\end{displaymath}](img896.png) |
(305) |
bem como
![\begin{displaymath}[\hat{l}_x,\hat{T}_{+}]=-\hat{T}_z
\end{displaymath}](img897.png) |
(306) |
![\begin{displaymath}[\hat{l}_y,\hat{T}_{+}]=-i\hat{T}_z
\end{displaymath}](img898.png) |
(307) |
Vamos agora calcular o comutador
![$[\hat{\vec{l}}^2,\hat{T}_{+}]$](img899.png) .
Lembrando que
.
Lembrando que
e usando as relações acima, temos, após um pouco de paciência,
![\begin{displaymath}[\hat{\vec{l}}^2,\hat{T}_{+}]=2[\hat{T}_{+}\hat{l}_z-\hat{T}_z\hat{l}_{+}]+2\hat{T}_{+}
\end{displaymath}](img901.png) |
(308) |
Sejam 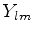 as autofunções de
as autofunções de
 e, em
particular, seja
e, em
particular, seja 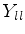 aquela com máximo valor de
aquela com máximo valor de  , para um
dado
, para um
dado 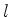 . Vamos mostrar que
. Vamos mostrar que
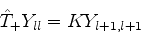 |
(309) |
onde 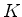 é uma constante.
é uma constante.
 |
(310) |
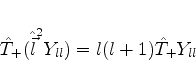 |
(311) |
![\begin{displaymath}
\hat{T}_{+}\hat{\vec{l}}^2 =
\hat{T}_{+}\hat{\vec{l}}^2...
...}=
[\hat{T}_{+},\hat{\vec{l}}^2]+\hat{\vec{l}}^2\hat{T}_{+}
\end{displaymath}](img908.png) |
(312) |
![\begin{displaymath}[\hat{T}_{+},\hat{\vec{l}}^2]Y_{ll}+
\hat{\vec{l}}^2(\hat{T}_{+}Y_{ll})=l(l+1)Y_{ll}
\end{displaymath}](img909.png) |
(313) |
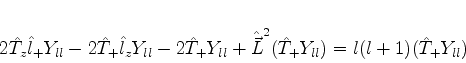 |
(314) |
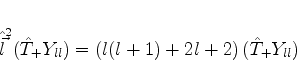 |
(315) |
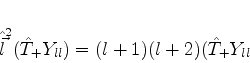 |
(316) |
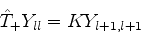 |
(317) |
Para determinar
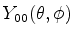 note-se que
note-se que
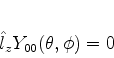 |
(318) |
e
Daí segue facilmente que
Dessas duas e da Eq.(318), segue que
 |
(321) |
para  . Isto quer dizer que
. Isto quer dizer que 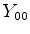 é invariante por
rotações infinitesimais em torno dos eixos
é invariante por
rotações infinitesimais em torno dos eixos 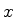 ,
, 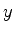 ,
, 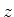 , ou seja,
é invariante por qualquer rotação infinitesimal. Logo, é
esfericamente simétrica, não podendo depender de
, ou seja,
é invariante por qualquer rotação infinitesimal. Logo, é
esfericamente simétrica, não podendo depender de 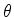 ou
ou
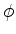 . Mas essas são as suas únicas variáveis. Portanto,
. Mas essas são as suas únicas variáveis. Portanto, 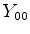 é constante. A menos de normalização , podemos então tomar
é constante. A menos de normalização , podemos então tomar
Considere o operador vetorial 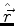 , e vamos construir o operador
, e vamos construir o operador
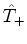 associado a ele, que seria o operador
associado a ele, que seria o operador
Como os operadores  e
e 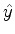 são multiplicativos,
vamos cometer um ligeiro abuso de notação, omitindo a
``casinha''(acento circunflexo, versão chinesa). Assim,
escreveremos, sem a menor cerimônia,
são multiplicativos,
vamos cometer um ligeiro abuso de notação, omitindo a
``casinha''(acento circunflexo, versão chinesa). Assim,
escreveremos, sem a menor cerimônia,
deixando claro que se trata de operadores. Já que estamos com a mão na massa,
vamos estudar, em lugar de 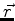 , o operador
, o operador
 . O operador
. O operador
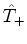 associado a ele é
associado a ele é
 |
(322) |
Temos, então,
 |
(323) |
ou seja,
 |
(324) |
ou ainda,
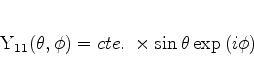 |
(325) |
De uma maneira geral, teremos:
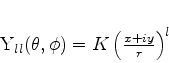 |
(326) |
Para obter 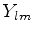 basta fazer uso do operador
basta fazer uso do operador 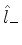 .
.
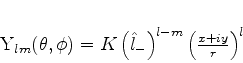 |
(327) |
A determinação de 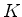 é feita pela normalização dos
é feita pela normalização dos 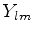 ,
,
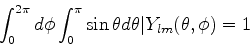 |
(328) |
Toma-se usualmente  real, o que fornece a seguinte tabela de harmônicos esféricos:
real, o que fornece a seguinte tabela de harmônicos esféricos:
e assim por diante.
1. Prove que
![$[AB,C] = A[B,C] + [A,C]B$](img946.png)
2. Prove que, se ![$[H,l_i]=0$](img947.png) então
então
![$[H, \exp{\frac{i}{\hbar}\theta \hbar l_i}]=0$](img948.png) ,
com
,
com
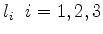 sendo as componentes do operador de momento angular. De fato, o resultado
vale para qualquer operador que comute com o hamiltoniano
sendo as componentes do operador de momento angular. De fato, o resultado
vale para qualquer operador que comute com o hamiltoniano 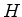 , e, portanto, para o
próprio
, e, portanto, para o
próprio 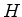 . Enuncie e comente este último caso. Mais precisamente, mostre que
é sempre verdade que
. Enuncie e comente este último caso. Mais precisamente, mostre que
é sempre verdade que
![$[\hat{H}, \exp{-\frac{i}{\hbar}\hat{H}t}]=0$](img950.png) .
.
3. Mostre que o operador
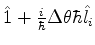 ``roda''
o sistema de um ângulo infinitesimal
``roda''
o sistema de um ângulo infinitesimal 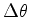 em torno do eixo
em torno do eixo  . A generalização
para ângulos
. A generalização
para ângulos 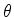 arbitrários é
arbitrários é
 .
Seja
.
Seja
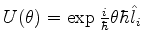 . Vimos no exercício anterior
que, se
. Vimos no exercício anterior
que, se ![$[H,l_i]=0$](img947.png) , então
, então
![$[H,U(\theta)]=0$](img956.png) . Seja
. Seja 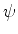 tal que
tal que 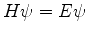 ,e
considere
,e
considere
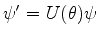 . Mostre que
. Mostre que
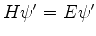 , com o mesmo
, com o mesmo
 anterior. Chegue a uma conclusão análoga usando o último resultado do exercício 2.
anterior. Chegue a uma conclusão análoga usando o último resultado do exercício 2.
4. Mostre que se a energia potencial de um sistema é 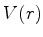 , independente de
, independente de 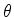 e
e 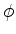 ,
então
,
então ![$[H,l_i]=0$](img947.png) , para
, para 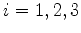 .
.
5. Mostramos no curso que
que, trocado em miúdos, quer dizer que
(a) Escreva os demais elementos de matriz dessa forma.
(b)Considere o harmônico esférico
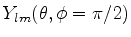 .
Temos
.
Temos
Por outro lado,
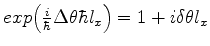 e,
usando os elementos de matriz acima,
e,
usando os elementos de matriz acima,
Logo,
Verifique cuidadosamente o argumento acima (o professor já está meio
velho...) e depois teste-o no caso particular l=1. Neste caso os harmônicos
esféricos são:
Henrique Fleming 2003

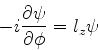
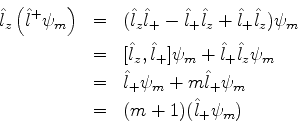
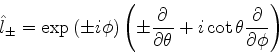
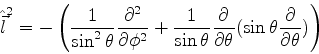
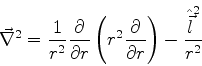
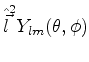
![]() são as funções
são as funções
![]() para
qualquer inteiro
para
qualquer inteiro ![]() . Quando construirmos as autofunções comuns a
. Quando construirmos as autofunções comuns a
![]() e
e ![]() , veremos que
, veremos que ![]() sofrerá mais restrições. De fato, como temos
sofrerá mais restrições. De fato, como temos
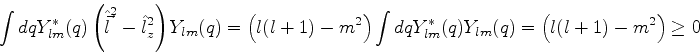
![]() ,
,
![]() um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
![$[\hat{\vec{l}}^2,\hat{T}_{+}]$](img899.png) .
Lembrando que
.
Lembrando que
![]() note-se que
note-se que
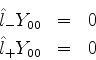
![]()
![]() então
então
![]() ,
com
,
com
![]() sendo as componentes do operador de momento angular. De fato, o resultado
vale para qualquer operador que comute com o hamiltoniano
sendo as componentes do operador de momento angular. De fato, o resultado
vale para qualquer operador que comute com o hamiltoniano ![]() , e, portanto, para o
próprio
, e, portanto, para o
próprio ![]() . Enuncie e comente este último caso. Mais precisamente, mostre que
é sempre verdade que
. Enuncie e comente este último caso. Mais precisamente, mostre que
é sempre verdade que
![]() .
.
![]() ``roda''
o sistema de um ângulo infinitesimal
``roda''
o sistema de um ângulo infinitesimal ![]() em torno do eixo
em torno do eixo ![]() . A generalização
para ângulos
. A generalização
para ângulos ![]() arbitrários é
arbitrários é
![]() .
Seja
.
Seja
![]() . Vimos no exercício anterior
que, se
. Vimos no exercício anterior
que, se ![]() , então
, então
![]() . Seja
. Seja ![]() tal que
tal que ![]() ,e
considere
,e
considere
![]() . Mostre que
. Mostre que
![]() , com o mesmo
, com o mesmo
![]() anterior. Chegue a uma conclusão análoga usando o último resultado do exercício 2.
anterior. Chegue a uma conclusão análoga usando o último resultado do exercício 2.
![]() , independente de
, independente de ![]() e
e ![]() ,
então
,
então ![]() , para
, para ![]() .
.