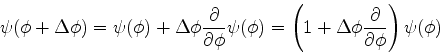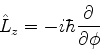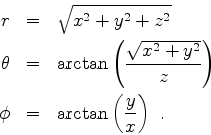Rotações e o momento angular
Uma partícula de massa 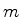 está em um estado de função de onda
está em um estado de função de onda
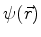 . Vamos executar uma rotação infinitesimal
. Vamos executar uma rotação infinitesimal
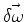 sobre o sistema.16 Em sua nova posição, a
função de onda será
sobre o sistema.16 Em sua nova posição, a
função de onda será
desprezando-se os termos a partir dos quadráticos em
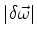 . Como
. Como
podemos escrever
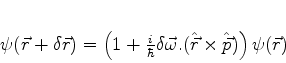 |
(265) |
Denotando o operador
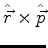 por
por
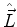 , temos
, temos
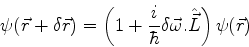 |
(266) |
O operador 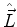 é denominado momento
angular, e é escrito, mais detalhadamente, como
é denominado momento
angular, e é escrito, mais detalhadamente, como
Da Eq.(264) se tira a expressão
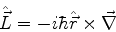 |
(267) |
ou, para as componentes,
Como 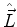 é hermiteano (por que?),
é hermiteano (por que?),
é unitário, e é a parte infinitesimal de
que, atuando sobre a função de onda de um sistema, produz a função
de onda do mesmo, rodado de
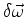 .
.
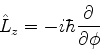 |
(271) |
A expressão explícita dos operadores 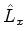 ,
, 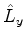 e
e
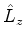 em coordenadas esféricas pode também ser obtida
diretamente da Eq.(270) utilizando as fórmulas de
transformação
em coordenadas esféricas pode também ser obtida
diretamente da Eq.(270) utilizando as fórmulas de
transformação
Trata-se de um cálculo simples mas trabalhoso. Vamos seguir um
caminho indireto mas mais iluminante. Primeiro, é conveniente
medir o momento angular em unidades de 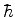 , isto é, introduzir
o operador
, isto é, introduzir
o operador 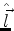 tal que
tal que
onde , de novo,
As expressões para as componentes de 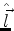 são, como
segue de (270),
são, como
segue de (270),
Por um cálculo direto, ou pelo uso da regra de Dirac17 obtêm-se:
![\begin{displaymath}[\hat{l}_a,\hat{l}_b]=i\epsilon_{abc}\hat{l}_c
\end{displaymath}](img819.png) |
(275) |
Como as componentes 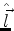 não comutam entre si, não há
autofunções comuns dessas componentes. Introduzindo o
momento angular total
não comutam entre si, não há
autofunções comuns dessas componentes. Introduzindo o
momento angular total
observamos que
Como
![\begin{displaymath}[\hat{l}_{x}^{2},\hat{l}_x]= 0
\end{displaymath}](img822.png) |
(276) |
![\begin{displaymath}[\hat{l}_{y}^{2},\hat{l}_x]= -i \hat{l}_{y} \hat{l}_{z} -i
\hat{l}_{z} \hat{l}_{y}
\end{displaymath}](img823.png) |
(277) |
![\begin{displaymath}[\hat{l}_{z}^{2},\hat{l}_x]
= i \hat{l}_z \hat{l}_y +i\hat{l}_y\hat{l}_z
\end{displaymath}](img824.png) |
(278) |
segue que
A direção 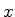 não tendo nenhum privilégio, segue que:
não tendo nenhum privilégio, segue que:
Sendo assim, podemos construir autofunções comuns a
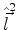 e uma das componentes de
e uma das componentes de 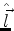 . Por
causa da expressão simples de
. Por
causa da expressão simples de 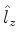 em coordenadas
esféricas, escolhemos o par
em coordenadas
esféricas, escolhemos o par
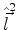 ,
,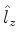 .
Henrique Fleming 2003
.
Henrique Fleming 2003