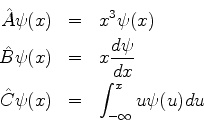Subsections
Operadores unitários e
simetrias
As quantidades observáveis (resultados de medidas) aparecem, na
mecânica quântica, sob a forma de produtos escalares de estados,
Um caso particular importante é um ``elemento de matriz'' de um
operador  :
:
Como toda teoria, a mecânica quântica admite transformações ``de
linguagem'': por exemplo, quando eu descrevo o mesmo fenômeno
usando dois sistemas de eixos ortogonais, obtenho descrições
distintas do mesmo fenômeno. Essas descrições devem ser
equivalentes, já que representam a mesma coisa de pontos-de-vista
distintos. É como se eu descrevesse o mesmo fenômeno em inglês e
em alemão: as descrições são diferentes, mas têm o mesmo conteúdo.
Como as quantidades físicas são representadas pelos produtos
escalares de estados, é importante o estudo dos operadores que
conservam os produtos escalares, ou seja, dos operadores 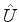 que são tais que
que são tais que
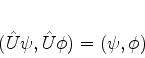 |
(258) |
ou, mais explicitamente,
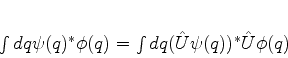 |
(259) |
Um operador linear é unitário, por definição, se
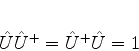 |
(260) |
Seja 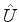 um operador unitário e considere as transformações
de funções de onda:
um operador unitário e considere as transformações
de funções de onda:
Então,
o que mostra que uma transformação implementada por um operador
unitário conserva os produtos escalares. Mais detalhadamente,
considere o produto escalar
Sejam
Podemos escrever
Logo,
Podemos interpretar este resultado assim: considere as
transformações
Então, temos:
onde
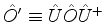 é a
transformação de
é a
transformação de  pela ação do operador linear
pela ação do operador linear 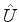 .
Diz-se que um operador
.
Diz-se que um operador  é invariante por uma
transformação unitária
é invariante por uma
transformação unitária 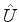 se
se
ou, equivalentemente, se
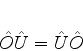 |
(261) |
O leitor verificará sem dificuldade que o operador 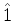 ,
definido por
,
definido por
é unitário. Para dar exemplos mais ricos, precisaremos definir a
exponencial de um operador.
Define-se 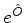 assim:
assim:
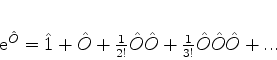 |
(262) |
onde, naturalmente, se pode escrever 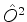 em vez de
em vez de
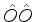 , etc. A idéia é usar a expansão da função
exponencial numérica como modelo da expansão do operador.
Usando-se esta definição, pode-se demonstrar a importante relação
de Baker-Hausdorff-Campbell:
, etc. A idéia é usar a expansão da função
exponencial numérica como modelo da expansão do operador.
Usando-se esta definição, pode-se demonstrar a importante relação
de Baker-Hausdorff-Campbell:
![\begin{displaymath}
e^{\hat{A}}\hat{B}e^{-\hat{A}} =
\hat{B} +
[\hat{A},\...
...}]]+
\frac{1}{3!}[\hat{A},[\hat{A},[\hat{A},\hat{B}]]]+ ...
\end{displaymath}](img724.png) |
(263) |
Uma aplicação imediata é esta: para  , temos
, temos
pois
![$[\hat{A},\hat{1}]=0$](img727.png) . Logo,
. Logo, 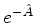 é o operador
inverso de
é o operador
inverso de 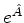 .
.
Considere um operador da forma 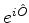 , com
, com
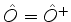 , ou seja, hermiteano. Temos então,
, ou seja, hermiteano. Temos então,
Logo,
ou seja, 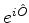 é unitário se
é unitário se  for hermiteano.
for hermiteano.
Exemplo: os seguintes operadores são unitários:
Chama-se operadores unitários infinitesimais operadores da forma
com
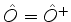 . Note-se que um operador desse tipo é o
truncamento da série que define o operador unitário
. Note-se que um operador desse tipo é o
truncamento da série que define o operador unitário
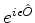 que mantém apenas os dois primeiros termos. Ou seja, um
operador unitário infinitesimal satisfaz a condição de unitaridade
desde que se desprezem termos que contenham potências quadráticas
de
que mantém apenas os dois primeiros termos. Ou seja, um
operador unitário infinitesimal satisfaz a condição de unitaridade
desde que se desprezem termos que contenham potências quadráticas
de  ou maiores. Explicitamente, temos, se
ou maiores. Explicitamente, temos, se
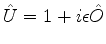 ,
,
 ,
e
,
e
Seja  um operador invariante por uma transformação
implementada pelo operador unitário infinitesimal
um operador invariante por uma transformação
implementada pelo operador unitário infinitesimal
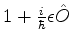 . Então
. Então
Logo, devemos ter
![$[\hat{O},\hat{B}]=0$](img744.png) . Sumarizando:
. Sumarizando:
Seja  invariante pela transformação unitária
invariante pela transformação unitária
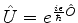 . Então,
. Então,
![$[\hat{B},\hat{O}]=0$](img746.png) .
.
Define-se simetria de um sistema com hamiltoniano
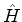 uma transformação unitária que deixa o hamiltoniano
invariante. Seja
uma transformação unitária que deixa o hamiltoniano
invariante. Seja
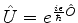 uma
simetria. Então, por definição,
uma
simetria. Então, por definição,
![$[\hat{H},\hat{O}]=0$](img747.png) . Ora, isto
significa que o operador
. Ora, isto
significa que o operador
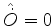 , ou, em outras
palavras,que a quantidade física associada ao operador hermiteano
, ou, em outras
palavras,que a quantidade física associada ao operador hermiteano
 é conservada. Desta forma associamos simetrias a leis de
conservação : a cada simetria corresponde uma quantidade
conservada. Este resultado, na física clássica, é conhecido como o
teorema de Noether.
é conservada. Desta forma associamos simetrias a leis de
conservação : a cada simetria corresponde uma quantidade
conservada. Este resultado, na física clássica, é conhecido como o
teorema de Noether.
1.(a)Construa o adjunto do operador
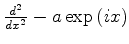 onde
onde 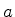 é um número real.
é um número real.
(b) Mostre que
![$[\vec{p},f(\vec{r})]=\frac{\hbar}{i}\vec{\nabla}f(\vec{r})$](img750.png) .
.
2. Os três operadores 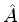 ,
,  e
e 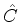 são dados por
são dados por
(i)Calcule
![$[\hat{A},\hat{B}]$](img754.png) e
e
![$[\hat{B},\hat{C}]$](img755.png) .
.
(ii)Resolva o problema de autovalores
exigindo que 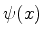 seja normalizável. Que restrição isto impõe
sobre
seja normalizável. Que restrição isto impõe
sobre 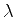 ?
?
3. Determine o operador unitário que efetua, sobre a função de onda de
um sistema, uma translação espacial
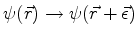 ,
onde
,
onde
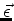 é um ``vetor infinitesimal''. Usando o fato de que uma sucessão
de translações independe da ordem em que são realizadas, demonstre que os operadores de
momento
é um ``vetor infinitesimal''. Usando o fato de que uma sucessão
de translações independe da ordem em que são realizadas, demonstre que os operadores de
momento 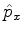 ,
, 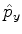 e
e 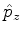 comutam. Aproveite para mostrar que esses
operadores são hermiteanos, sem calcular qualquer integral.
comutam. Aproveite para mostrar que esses
operadores são hermiteanos, sem calcular qualquer integral.
Henrique Fleming 2003
![]() que são tais que
que são tais que
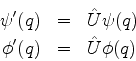
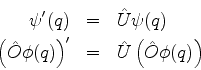
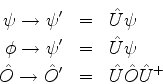
![]() assim:
assim:
![]() , com
, com
![]() , ou seja, hermiteano. Temos então,
, ou seja, hermiteano. Temos então,
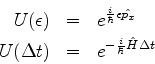
![]() invariante pela transformação unitária
invariante pela transformação unitária
![]() . Então,
. Então,
![]() .
.
![]() uma transformação unitária que deixa o hamiltoniano
invariante. Seja
uma transformação unitária que deixa o hamiltoniano
invariante. Seja
![]() uma
simetria. Então, por definição,
uma
simetria. Então, por definição,
![]() . Ora, isto
significa que o operador
. Ora, isto
significa que o operador
![]() , ou, em outras
palavras,que a quantidade física associada ao operador hermiteano
, ou, em outras
palavras,que a quantidade física associada ao operador hermiteano
![]() é conservada. Desta forma associamos simetrias a leis de
conservação : a cada simetria corresponde uma quantidade
conservada. Este resultado, na física clássica, é conhecido como o
teorema de Noether.
é conservada. Desta forma associamos simetrias a leis de
conservação : a cada simetria corresponde uma quantidade
conservada. Este resultado, na física clássica, é conhecido como o
teorema de Noether.