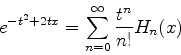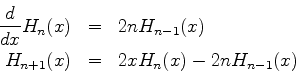Subsections
O oscilador harmônico
Uma partícula de massa  executa movimento unidimensional sob a ação de
uma força elástica
executa movimento unidimensional sob a ação de
uma força elástica 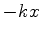 . Isto é um oscilador harmônico. Sua energia potencial
é
. Isto é um oscilador harmônico. Sua energia potencial
é
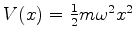 , e. portanto, a equação de Schrödinger
para estados estacionário é
, e. portanto, a equação de Schrödinger
para estados estacionário é
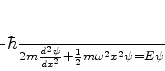 |
(209) |
Note-se que
 .
.
A Eq.(209) pode ser escrita na forma
![\begin{displaymath}
\frac{1}{2m}\left[\left(\frac{\hbar}{i}\frac{d}{dx}\right)^2
+\left(m\omega x\right)^2\right]\psi=E\psi
\end{displaymath}](img579.png) |
(210) |
Daqui se vê que
![\begin{displaymath}
\hat{H}=\frac{1}{2m}\left[\left(\frac{\hbar}{i}\frac{d}{dx}\right)^2
+\left(m\omega x\right)^2\right]
\end{displaymath}](img580.png) |
(211) |
Considere os operadores
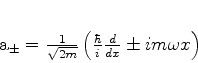 |
(212) |
Um cálculo simples mostra que
 |
(213) |
de maneira que, usando (211),
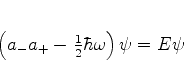 |
(214) |
Um outro cálculo simples resulta em
![\begin{displaymath}[a_{-},a_{+}]=\hbar\omega
\end{displaymath}](img584.png) |
(215) |
A Eq.(214) dá
Lema 1: Seja  um estado estacionário do oscilador harmônico de energia
um estado estacionário do oscilador harmônico de energia
 . Então
. Então  é um estado estacionário de energia
é um estado estacionário de energia 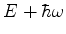 .
.
Dem.:
Ou,
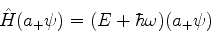 |
(217) |
Analogamente se mostra que
 |
(218) |
Lema 2: A energia do oscilador harmônico é 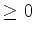 .
.
Dem.: Esta demonstração depende de um Lema, demonstrado mais
adiante,15 junto à Eq.(290). Como  pode
ser escrito como a soma de dois operadores hermiteanos ao
quadrado,
pode
ser escrito como a soma de dois operadores hermiteanos ao
quadrado,
segue que
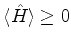 . Como os autovalores de
um operador são casos particulares de seus valores médios (quando
os estados são as autofunções), a desigualdade acima proíbe a
existência de autovalores negativos do hamiltoniano.
. Como os autovalores de
um operador são casos particulares de seus valores médios (quando
os estados são as autofunções), a desigualdade acima proíbe a
existência de autovalores negativos do hamiltoniano.
Em decorrência disso, deve haver um estado 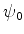 tal que
tal que
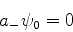 |
(219) |
De fato, se não fosse assim, dada qualquer autofunção do hamiltoniano
do oscilador harmônico, a aplicação a ela do operador 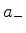 geraria
uma outra autofunção , de energia menor, o processo podendo se repetir
indefinidamente, até se chegar a energia s negativas, o que é proibido.
geraria
uma outra autofunção , de energia menor, o processo podendo se repetir
indefinidamente, até se chegar a energia s negativas, o que é proibido.
Explicitamente esta última equação é
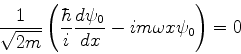 |
(220) |
Esta é a função de onda do estado estacionário do oscilador harmônico.
A energia desse estado é obtida assim:
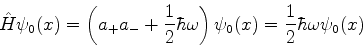 |
(222) |
Logo, temos
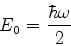 |
(223) |
O estado de energia imediatamente mais alta, chamado de primeiro
estado excitado, tem a função de onda
 |
(224) |
ou
 |
(225) |
e possui energia
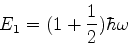 |
(226) |
Mais geralmente,
 |
(227) |
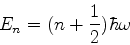 |
(228) |
e, com algum esforço, pode-se mostrar que
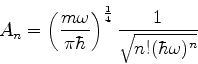 |
(229) |
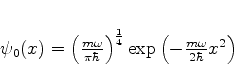 |
(230) |
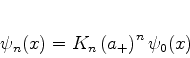 |
(231) |
 |
(232) |
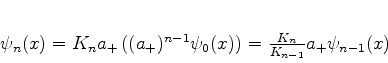 |
(233) |
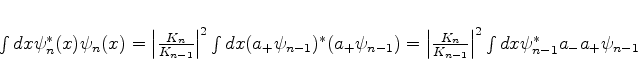 |
(234) |
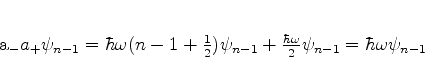 |
(235) |
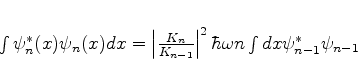 |
(236) |
 |
(237) |
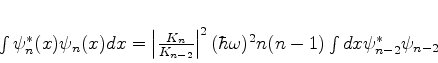 |
(238) |
 |
(239) |
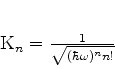 |
(240) |
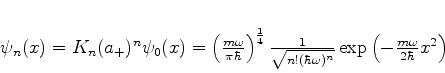 |
(241) |
Um oscilador harmônico que não oscila é decepcionante. Se
calcularmos o valor médio da posição,
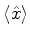 ,
nos estados estacionários do oscilador harmônico, que vimos até
agora, encontraremos (e o leitor deve obter isso por conta
própria!)
,
nos estados estacionários do oscilador harmônico, que vimos até
agora, encontraremos (e o leitor deve obter isso por conta
própria!)
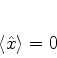 |
(242) |
ou seja, nenhuma oscilação! Estados estacionários não são
apropriados para comparar o sistema quântico com o análogo
clássico. Para obter alguma coisa semelhante a um pêndulo, devemos
estudar pacotes de onda. Os particulares pacotes de onda que
vamos estudar agora se chamam estados coerentes.
Consideremos as autofunções do operador 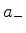 , introduzido
acima. Como
, introduzido
acima. Como 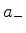 não comuta com
não comuta com  , as autofunções de
, as autofunções de
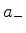 não serão, em geral, autofunções de
não serão, em geral, autofunções de  , ou seja,
não serão estados estacionários. Sejam então
, ou seja,
não serão estados estacionários. Sejam então 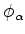 funções tais que
funções tais que
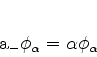 |
(243) |
Como o operador 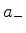 não é hermiteano, os autovalores
não é hermiteano, os autovalores 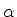 serão números complexos quaisquer.
serão números complexos quaisquer.
Lembremos que os estados estacionários podem ser escritos em
termos do estado fundamental assim:
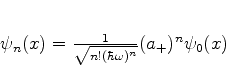 |
(244) |
Vai ser importante nos cálculos que faremos a seguir a seguinte
quantidade:
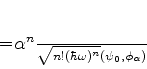 |
(245) |
Vamos agora expandir
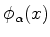 em estados estacionários.
Para simplificar a notação, vamos introduzir a abreviação
em estados estacionários.
Para simplificar a notação, vamos introduzir a abreviação
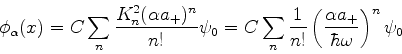 |
(247) |
A constante 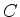 é determinada normalizando-se
é determinada normalizando-se
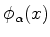 ,
como segue:
,
como segue:
Logo,
Voltando à expansão,
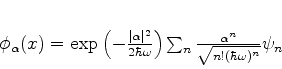 |
(248) |
Para obter a dependência temporal de
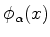 precisamos
demonstrar um resultado geral:
precisamos
demonstrar um resultado geral:
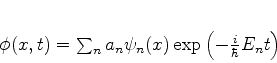 |
(249) |
Aplicando este teorema à Eq.(248), temos
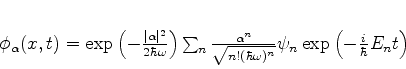 |
(250) |
ou
Comparando com a Eq.(248), vê-se que:
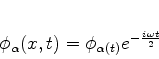 |
(252) |
com
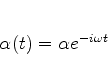 |
(253) |
Podemos agora calcular
 no estado
no estado
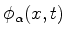 .
.
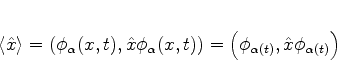 |
(254) |
Da definição de  e
e 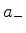 obtém-se facilmente que
obtém-se facilmente que
logo,
 |
(255) |
Mas
e, como  é o adjunto de
é o adjunto de 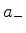 ,
,
Logo,
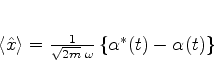 |
(256) |
Pondo
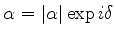 , temos
, temos
e
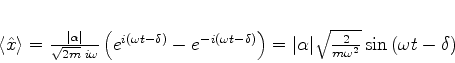 |
(257) |
e surgiu finalmente a oscilação procurada! O valor médio da
posição, nesse estado, oscila exatamente como no caso clássico.
Para uso nos exercícios subseqüentes, apresentamos aqui uma tabela
de funções de onda de estados estacionários do oscilador harmônico.
onde
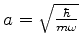 .
.
1.(a) Mostre que o parâmetro 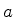 que aparece na tabela é igual
ao deslocamento máximo de um oscilador clássico de energia
que aparece na tabela é igual
ao deslocamento máximo de um oscilador clássico de energia
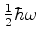 .
.
(b) Verifique que a expressão
 satisfaz a equação
de Schrödinger para o movimento harmônico simples com energia
satisfaz a equação
de Schrödinger para o movimento harmônico simples com energia
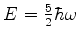 . Qual o valor para
. Qual o valor para 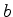 ?
?
2. Considere o meio-oscilador harmônico, isto é, uma partícula
cuja energia potencial é
(a) Compareas funções de onda dos estados estacionários deste sistema
com as do oscilador harmônico normal com os mesmos valores de  e
e 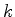 .
.
(b) Quais são as energia s permitidas para o meio-oscilador?
(c) Invente um sistema que seria o análogo macroscópico deste sistema
quântico.
3. Regiões classicamente proibidas para o oscilador harmônico simples.
Usando a função de onda normalizada para o estado fundamental do oscilador
harmônico, calcule a probabilidade de que uma observação da posição detete
a partícula numa região classicamente proibida. A integral que você
obterá não pode ser resolvida analiticamente. Olhe o resultado numérico
numa tabela da error function, ou nos programas Maple ou Mathematica.
4. A tabela exibe as funções 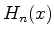 , denominadas polinômios de Hermite.
, denominadas polinômios de Hermite.
(a)Mostre que 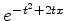 é uma função geratriz dos polinômios de
Hermite, isto é, que
é uma função geratriz dos polinômios de
Hermite, isto é, que
ao menos até  . Determine
. Determine 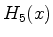 .
.
(b) Tomando a derivada desta expressão, demonstre as relações de recorrência
5. Valendo-se da expressão das funções de onda do oscilador harmônico,
mostre que devemos esperar que
Henrique Fleming 2003

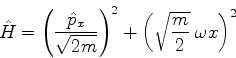
![]() tal que
tal que
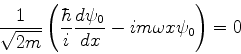
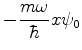
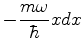
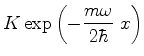

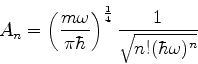
![]() a
autofunção normalizada do estado fundamental do oscilador
harmônico. Então,
a
autofunção normalizada do estado fundamental do oscilador
harmônico. Então,
![]() ,
nos estados estacionários do oscilador harmônico, que vimos até
agora, encontraremos (e o leitor deve obter isso por conta
própria!)
,
nos estados estacionários do oscilador harmônico, que vimos até
agora, encontraremos (e o leitor deve obter isso por conta
própria!)

![]() em estados estacionários.
Para simplificar a notação, vamos introduzir a abreviação
em estados estacionários.
Para simplificar a notação, vamos introduzir a abreviação
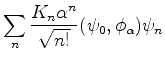



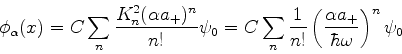
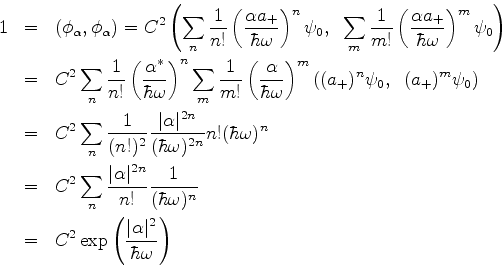
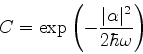
![]() satisfaz a
equação de Schrödinger
satisfaz a
equação de Schrödinger
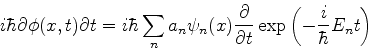
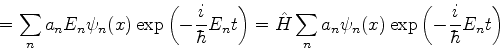
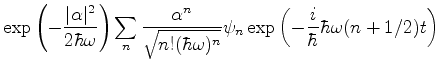
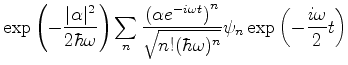
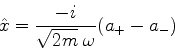
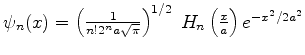
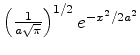

![$
\left(\frac{1}{8a\sqrt{\pi}}\right)^{1/2}\left[2-4\left(\frac{x}{a}\right)^2\right]e^{-x^2/2a^2}$](img685.png)
![$\left(\frac{1}{48 a \sqrt{\pi}}\right)^{1/2}
\left[12\left(\frac{x}{a}\right)-8\left(\frac{x}{a}\right)^3\right]e^{-x^2/2a^2}$](img687.png)
![$\left(\frac{1}{384 a
\sqrt{\pi}}\right)^{1/2}\left[12 -
48\left(\frac{x}{a}\right)^2+16\left(\frac{x}{a}\right)^4\right]e^{-x^2/2a^2}$](img689.png)
![]() que aparece na tabela é igual
ao deslocamento máximo de um oscilador clássico de energia
que aparece na tabela é igual
ao deslocamento máximo de um oscilador clássico de energia
![]() .
.
![]() satisfaz a equação
de Schrödinger para o movimento harmônico simples com energia
satisfaz a equação
de Schrödinger para o movimento harmônico simples com energia
![]() . Qual o valor para
. Qual o valor para ![]() ?
?