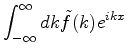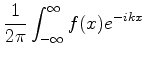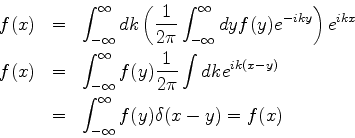Subsections
A função delta de Dirac
Considere a função
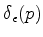 , definida assim:
, definida assim:
Temos, claramente,
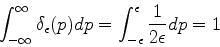 |
(181) |
Seja 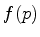 uma função contínua. Então,
uma função contínua. Então,
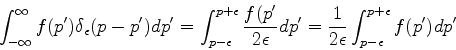 |
(182) |
No limite para
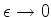 , esta última integral dá
, esta última integral dá
de forma que a Eq.(182) pode ser escrita
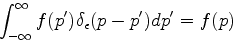 |
(183) |
A função delta de Dirac, 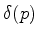 é definida, simbolicamente,
como o limite, para
é definida, simbolicamente,
como o limite, para
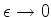 , da função
, da função
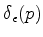 . Suas propriedades, que podem ser motivadas
por esse limite, podem ser sintetizadas assim:
. Suas propriedades, que podem ser motivadas
por esse limite, podem ser sintetizadas assim:
Nessas relações a integral não precisa realmente ir de 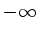 a
a
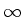 . Basta que seja em um intervalo que contenha o ponto em
que o argumento da função delta se anula.
. Basta que seja em um intervalo que contenha o ponto em
que o argumento da função delta se anula.
http://denebola.if.usp.br/~jbarata/Notas_de_aula/arquivos/nc-cap12.pdf
Outras relações importantes envolvendo a ``função delta'' são as
seguintes:
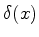 |
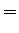 |
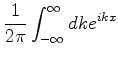 |
(184) |
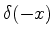 |
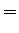 |
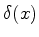 |
(185) |
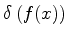 |
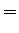 |
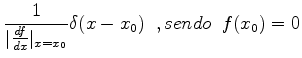 |
(186) |
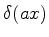 |
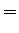 |
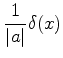 |
(187) |
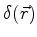 |
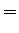 |
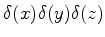 |
(188) |
onde, nesta última, se tem
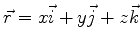 .
.
Integral de Fourier
A integral de Fourier é
instrumento fundamental na mecânica quântica. Trata-se de uma
extensão das séries de Fourier que permite obter expansões de
funções que não são periódicas. Este não é o lugar para se
adquirir fluência no uso, e uma boa compreensão dos métodos da
análise de Fourier. O leitor deverá dedicar algum estudo a este
tópico, presente em todos os livros de física-matemática. De minha
parte recomendo o livro de Arnold Sommerfeld, Partial
Differential Equations of Physics. Um belíssimo livro de
matemática sobre este mesmo tema, é Körner, Fourier
Analysis, um dos livros mais bonitos que já li.
A integral, ou transformada, de Fourier de uma função 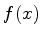 , é
uma função
, é
uma função 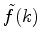 a ela ligada pelas relações
a ela ligada pelas relações
Pode-se verificar a consistência dessas relações com o uso da
funçao 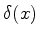 :
:
A transformada de Fourier de uma função constante, 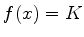 , é:
, é:
ou seja, a transformada de Fourier de uma constante é um múltiplo
de 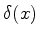 . Um outro resultado importante é a transformada de
Fourier de uma gaussiana: seja
. Um outro resultado importante é a transformada de
Fourier de uma gaussiana: seja
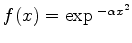 . Sua
transformada de Fourier é
. Sua
transformada de Fourier é
ou seja, a transformada de Fourier de uma gaussiana é outra
gaussiana.
Henrique Fleming 2003
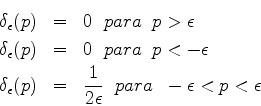

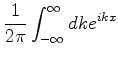
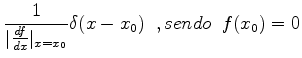
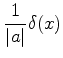
![]() , é
uma função
, é
uma função ![]() a ela ligada pelas relações
a ela ligada pelas relações