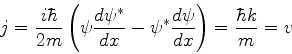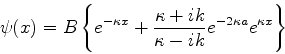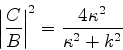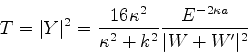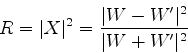Subsections
Uma partícula de massa  se move sob a ação
de um campo de forças que confere à partícula uma
energia potencial
se move sob a ação
de um campo de forças que confere à partícula uma
energia potencial  tal que
tal que
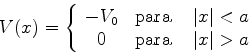 |
(71) |
como descrito na figura.
Vamos considerar primeiro o caso  , onde
, onde  é a energia
total da partícula. No caso clássico, a partícula não
pode atingir as regiões I e III. De fato, sua energia total é
é a energia
total da partícula. No caso clássico, a partícula não
pode atingir as regiões I e III. De fato, sua energia total é
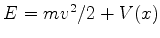 , ou seja,
, ou seja,
 . Nas regiões I e III
temos
. Nas regiões I e III
temos 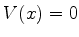 , o que daria
, o que daria 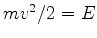 . Mas
. Mas  , o que daria uma
energia cinética negativa, impossível.10
, o que daria uma
energia cinética negativa, impossível.10
Na região II não há problema, pois teríamos
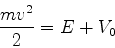 |
(72) |
e é possível ter energia cinética positiva mesmo com
 .
.
A equação de Schrödinger para os estados estacionários é
![\begin{displaymath}
\left[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+ V(x)\right]\phi(x)=E\phi(x)
\end{displaymath}](img296.png) |
(73) |
Para  ou
ou 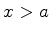 , temos
, temos 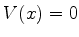 , e
, e
Pondo
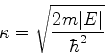 |
(76) |
temos
 |
(77) |
cuja solução geral é
 |
(78) |
Para 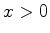 o termo em
o termo em 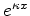 é inadequado, pois daria
uma probabilidade de localização da partícula tendendo
a infinito para
é inadequado, pois daria
uma probabilidade de localização da partícula tendendo
a infinito para
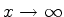 . Logo, temos de tomar
. Logo, temos de tomar
 . Assim,
. Assim,
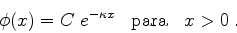 |
(79) |
Por um raciocínio análogo,
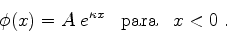 |
(80) |
Nas soluções acima  e
e  são constantes
arbitrárias, a determinar posteriormente.
são constantes
arbitrárias, a determinar posteriormente.
Na região interna, 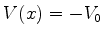 , e a equação é
, e a equação é
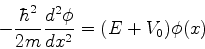 |
(81) |
ou
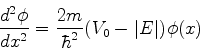 |
(82) |
Pondo
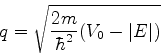 |
(83) |
temos a solução geral
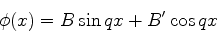 |
(84) |
A energia potencial  descrita acima é uma função
descontínua, e portanto não-diferenciável, nos pontos
descrita acima é uma função
descontínua, e portanto não-diferenciável, nos pontos 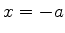 e
e  . A equação diferencial deve ser, então, tratada como 3
equações, uma para cada região onde
. A equação diferencial deve ser, então, tratada como 3
equações, uma para cada região onde  é contínua e
diferenciável. Por isso a resolvemos separadamente para as regiões
I, II e III.
O potencial descontínuo é uma idealização de um potncial
semelhante, mas de ``bordas arredondadas'', alguma coisa assim:
A razão prática para tratar o potencial idealizado, e não o
``real'', é que assim é muito mais fácil resolver a
equação diferencial.
é contínua e
diferenciável. Por isso a resolvemos separadamente para as regiões
I, II e III.
O potencial descontínuo é uma idealização de um potncial
semelhante, mas de ``bordas arredondadas'', alguma coisa assim:
A razão prática para tratar o potencial idealizado, e não o
``real'', é que assim é muito mais fácil resolver a
equação diferencial.
O preço que se paga pelo uso de um potencial descontínuo é:
como ``ligar'' entre si as soluções das três regiões? A
matemática nos dá a chave: como a equação diferencial é de
segunda ordem, sua solução é determinada dando-se, em um
ponto, o valor da função e de sua derivada primeira. Então,
para conectar as regiões, procedemos assim: em um ponto comum às
regiões I e II (este ponto é 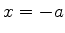 ) exigimos que
) exigimos que
 e
e
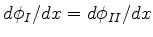 , onde
, onde 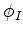 é a solução na região I, e
é a solução na região I, e 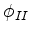 é a solução
na região II. Para conectar as regiões II e III, agimos da mesma
forma:
é a solução
na região II. Para conectar as regiões II e III, agimos da mesma
forma:
Em  ,
,
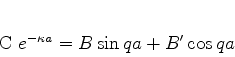 |
(85) |
 |
(86) |
Em 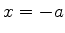 ,
,
É uma questão de técnica determinar as constantes. Dividindo
(85) por (87) temos:
 |
(89) |
Pondo 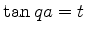 , temos
, temos
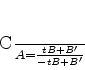 |
(90) |
Dividindo (86) por (88) temos
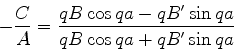 |
(91) |
ou
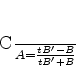 |
(92) |
Combinando (90) e (92), temos
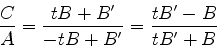 |
(93) |
De onde se tira sem dificuldade que
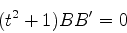 |
(94) |
Isto nos informa que temos ou 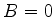 ou
ou 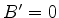 . Para
. Para 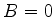 as
funções são, na região
as
funções são, na região
 , cosenos, ou seja,
são funções pares de
, cosenos, ou seja,
são funções pares de 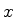 . Para
. Para  , são senos, ou
seja, funções ímpares de
, são senos, ou
seja, funções ímpares de 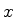 . Vamos tratar os dois casos
separadamente.
. Vamos tratar os dois casos
separadamente.
(i)  (funções ímpares).
(funções ímpares).
Note que  , pois
, pois
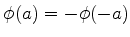 , já que a função é
ímpar.
, já que a função é
ímpar.
Para  temos as relações:
temos as relações:
É desnecessário fazer uso das relações em 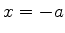 , porque,
sendo a função ímpar, elas repetem as relações em
, porque,
sendo a função ímpar, elas repetem as relações em  .
Dividindo a de cima pela de baixo, obtém-se:
.
Dividindo a de cima pela de baixo, obtém-se:
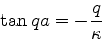 |
(100) |
É esta equção que irá determinar para que valores da energia
existem estados estacionários nesse poço. Equações deste tipo
(que não são equações algébricas11, e só em
raros casos podem ser resolvidas analiticamente. Este não é, infelizmente,
um desses raros casos. Recorre-se então a soluções numéricas.
Neste particular caso, porém, é possível usar um método
gráfico que ilustra muito bem as características gerais da solução.
Em primeiro lugar, vamos escrever (100) de outra forma. Introduzo as variáveis
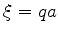 e
e
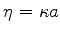 , que são tais que
, que são tais que
 |
(101) |
ou
 |
(102) |
Nessas variáveis, a equação (100) fica
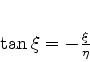 |
(103) |
Mas
 |
(104) |
logo,
![\begin{displaymath}
-\frac{\xi}{\eta}=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2-\xi^2\right]^{-\frac{1}{2}}
\end{displaymath}](img358.png) |
(105) |
e a equação (103) se escreve
![\begin{displaymath}
\tan{\xi}=-\xi\left[\frac{2m}{\hbar^2}V_{0}\;a^2-\xi^2\right]^{-\frac{1}{2}}
\end{displaymath}](img359.png) |
(106) |
Cada solução desta equação dá um valor de 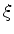 , e, portanto,
um valor de
, e, portanto,
um valor de 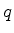 , ou seja, de
, ou seja, de 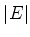 . Esta é, por isso, a equação para
os autovalores da energia .
. Esta é, por isso, a equação para
os autovalores da energia .
A idéia é a seguinte: traço os gráficos da função 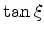 e
da função que está no segundo membro de (106). Onde as
curvas se cortem estarão os valores de
e
da função que está no segundo membro de (106). Onde as
curvas se cortem estarão os valores de 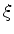 que são as soluções
de (106).
que são as soluções
de (106).
Para traçar a curva da função que está no segundo membro, vamos estudar
um pouco suas propriedades.
Vamos analisar a função
![\begin{displaymath}
f(\xi)=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2-\xi^2\right]^{-...
...{1}{2}}
=-\xi\left(\mathcal{A}^2-\xi^2\right)^{-\frac{1}{2}}
\end{displaymath}](img363.png) |
(107) |
Sua derivada pode ser escrita, após alguma álgebra,
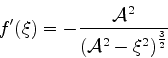 |
(108) |
e é sempre negativa, tornando-se  para
para
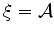 , isto é
, isto é
 |
(109) |
O gráfico abaixo contém as curvas 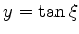 e
e
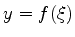 As soluções da equação
As soluções da equação
![\begin{displaymath}
\tan{\xi}=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2 -\xi^2\right]^{-\frac{1}{2}}
\end{displaymath}](img370.png) |
(110) |
são as interseções dessas duas curvas. Como 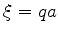 e
e
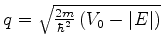 , os valores
de
, os valores
de 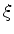 que satisfazem a equação acima permitem calcular os valores de
que satisfazem a equação acima permitem calcular os valores de
 correspondentes. Esses serão os valores possíveis para a energia
do sistema.
correspondentes. Esses serão os valores possíveis para a energia
do sistema.
Vemos assim que o número de autovalores da energia para os estados
ímpares é finito, podendo ser nulo (se
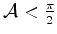 ).
).
(ii) (soluções pares).
(soluções pares).
Neste caso as equações ficam:
Comparando (111) com (113) vemos que  . Dividindo
(114) por (113) temos, então,
. Dividindo
(114) por (113) temos, então,
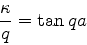 |
(115) |
e, introduzindo de novo as variáveis 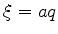 e
e
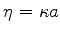 ,
,
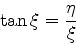 |
(116) |
com
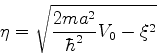 |
(117) |
de maneira que a equação que determina os autovalores da energia
é
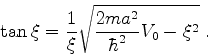 |
(118) |
Seja
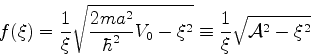 |
(119) |
Temos que
 (
( ) e
) e
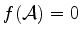 , e, ainda,
, e, ainda,
Podemos concluir então que o poço quadrado possui sempre soluções
de energia negativa. Os autovalores da energia de tais estados são discretos e
em número finito. O menor valor, correspondente ao estado fundamental,
ocorre para um estado cuja função de onda é par.
O interpretação probabilística da mecânica
quântica é introduzida pelo postulado de Born12, que diz que
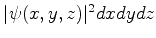 é a probabilidade de a partícula, cuja função de onda
é
é a probabilidade de a partícula, cuja função de onda
é 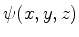 , estar, em um determinado instante, num elemento
de volume
, estar, em um determinado instante, num elemento
de volume  em torno do ponto de coordenadas
em torno do ponto de coordenadas 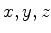 .
.
Queremos examinar o que ocorre com
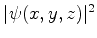 quando o
movimento da partícula é levado em conta.
quando o
movimento da partícula é levado em conta.
A equação de Schrödinger diz que
 |
(122) |
Tomando-se o complexo conjugado, termo a termo,
temos
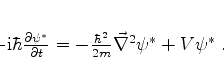 |
(123) |
Multiplicando (122) à direita por 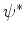 e (123) à esquerda por
e (123) à esquerda por 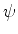 e subtraíndo,
obtemos
e subtraíndo,
obtemos
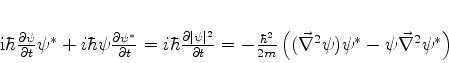 |
(124) |
O segundo membro pode ser posto numa forma mais transparente,
notando que
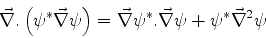 |
(125) |
ou
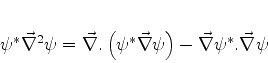 |
(126) |
Tomando o complexo conjugado desta relação:
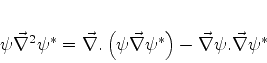 |
(127) |
Subtraíndo (127) de (126),
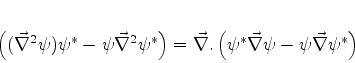 |
(128) |
Levando (128) ao segundo membro de
(124), chega-se a
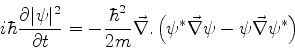 |
(129) |
Introduzindo as notações
temos, então,
 |
(132) |
que tem a forma da equação da continuidade, conhecida seja
da mecânica dos fluidos, onde explicita a conservação
da massa do fluido, seja do eletromagnetismo, onde faz o mesmo
para a conservação da carga. Poderíamos então dizer
que ela expressa, aqui, a conservação de probabilidade.
Assim como, no eletromagnetismo, a equação da continuidade
fornece detalhes sobre como se dá a conservação da carga
13, na mecânica quântica ela faz o mesmo com
a probabilidade.
Aqui convém adotar uma linguagem que, embora eqüivalente, é
mais familiar do que a que usamos até agora. Suponhamos que, em vez
de uma partícula, considerássemos um conjunto de réplicas
da partícula, idênticas, ou seja, com a mesma função
de onda, e independentes, isto é, que não interagem. Sejam 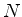 essas réplicas. Se normalizarmos a função de onda de modo que
essas réplicas. Se normalizarmos a função de onda de modo que
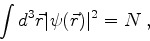 |
(133) |
estendendo-se a integral a todo o espaço, e considerarmos
um volume  delimitado por uma superfície
delimitado por uma superfície 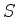 fechada,
a integral
fechada,
a integral
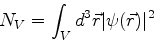 |
(134) |
dará, não a probabilidade de uma partícula estar em 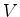 ,
mas o número
,
mas o número 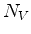 de partículas, das
de partículas, das 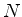 existentes,
que estão dentro de
existentes,
que estão dentro de 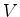 . Seja
. Seja 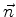 o campo das normais externas
à superfície
o campo das normais externas
à superfície 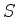 . Temos
. Temos
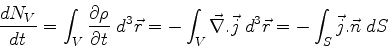 |
(135) |
onde, na última passagem, fizemos uso do teorema do divergente.
Suponhamos que 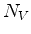 decresça com o tempo. Então
decresça com o tempo. Então
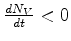 , e
, e
 |
(136) |
A Eq.(136) mede, portanto, o número de
partículas que, na unidade de tempo, saem do
volume 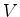 , atravessando a superfície
, atravessando a superfície 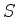 14(este saem, para ser mais preciso,
é o número de partículas que saem menos o de partículas
que entram, por unidade de tempo). Depreende-se disso que, se
14(este saem, para ser mais preciso,
é o número de partículas que saem menos o de partículas
que entram, por unidade de tempo). Depreende-se disso que, se
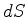 é um trecho infinitesimal de uma superfície, e se
é um trecho infinitesimal de uma superfície, e se
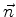 for uma normal a ela, então
for uma normal a ela, então
é o número (resultante) de partículas que atravessam 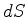 por unidade
de tempo no sentido indicado pela normal. Se o número for negativo,
o fluxo majoritário será no sentido de
por unidade
de tempo no sentido indicado pela normal. Se o número for negativo,
o fluxo majoritário será no sentido de 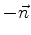 .
.
Uma partícula de massa  se move num campo de forças, com uma
energia potencial da forma
se move num campo de forças, com uma
energia potencial da forma
ou,
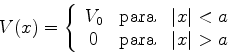
sendo sua energia total  localizada entre
localizada entre 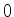 e
e 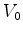 .
Vamos procurar seus estados estacionários. Para especificar mais
o problema, digamos que a partícula incide sobre a barreira
vindo da esquerda.
.
Vamos procurar seus estados estacionários. Para especificar mais
o problema, digamos que a partícula incide sobre a barreira
vindo da esquerda.
Se estivéssemos tratando de estados localizados (pacotes de onda),
a caracterização deste particular problema (incidência da esquerda
para a direita) seria trivial. Mas, para estados estacionários, isto é,
tais que a probabilidade de posição não depende do tempo, isto é mais
sutil. Recorramos a uma imagem clássica. Para conseguir um fenômeno análogo
(isto é, sem dependência temporal) na mecânica clássica, precisamos recorrer
a muitas partículas, incidindo sobre a barreira da esquerda para a direita.
Imaginemos um fluxo contínuo dessas partículas. Depois de um certo tempo,
teremos uma figura que não se altera mais, constituída por um certo número
de partículas incidindo sobre a barreira, superpostas a um fluxo de
partículas refletidas por ela. Embora cada partícula esteja se movendo,
o conjunto todo parece parado, no regime estacionário. O fato de as partículas
virem da esquerda pode ser descoberto, neste regime estacionário, pelo fato
de que há partículas refletidas à esquerda da barreira.
Passemos ao caso quântico. No regime estacionário esperamos ter, como no caso
clássico, ondas incidentes e ondas refletidas, à esquerda da barreira. Mas, e esta
é a principal diferença introduzida pela mecânica quântica neste problema,
pode haver ondas saindo da barreira, no lado direito. O que caracteriza,
então, o problema estacionário como advindo de uma partícula incidente
da esquerda para a direita é que, do lado direito da barreira, existem apenas
partículas afastando-se da barreira.
Para  temos as regiões I e III, onde a partícula não está sujeita
a nenhuma força. Nestes casos,
temos as regiões I e III, onde a partícula não está sujeita
a nenhuma força. Nestes casos,
 |
(137) |
ou
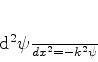 |
(138) |
onde usamos
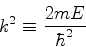 |
(139) |
A solução geral de (138) é
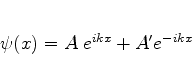 |
(140) |
e é um estado estacionário, portanto, com dependência temporal
dada por uma exponencial:
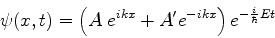 |
(141) |
onde
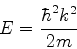 |
(142) |
A corrente de probabilidade
dá, para a as parcelas que constituem a função (140):
(i)Para
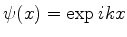 (
( ),
),
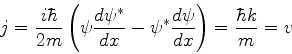 |
(143) |
ou seja, 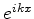 representa uma partícula com velocidade positiva, movendo-se
da esquerda para a direita.
representa uma partícula com velocidade positiva, movendo-se
da esquerda para a direita.
(ii) Para
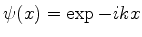 , temos
, temos 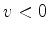 , e a partícula se move da direita para
a esquerda.
, e a partícula se move da direita para
a esquerda.
Para fixar o nosso problema, diremos então que, na região I teremos
 |
(144) |
que inclui a partícula incidente (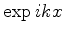 ) e a refletida
(
) e a refletida
(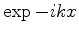 ).
).
Na região III tenderíamos a supor que a função de onda fosse
zero, baseando-se na mecânica clássica, pois uma partícula clássica
não pode atravessar a barreira: na zona II ela teria uma energia cinética
negativa! Porém, se fizessemos esta hipótese, não encontraríamos
solução. Pomos, então,
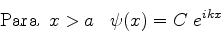 |
(145) |
que descreve uma partícula que, vindo da esquerda, ultrapassou a
barreira.
Finalmente, dentro da barreira (região II), a equação de
Schrödinger é
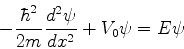 |
(146) |
ou
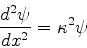 |
(147) |
com
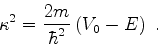 |
(148) |
A solução geral desta equação de Schrödinger é
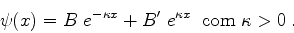 |
(149) |
Vamos denominar ``função de onda incidente'' ao termo
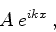 |
(150) |
``função de onda refletida'' ao termo
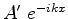 ,
e ``função de onda transmitida'' ao termo
,
e ``função de onda transmitida'' ao termo 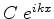 .
.
A densidade de corrente incidente é
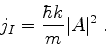 |
(151) |
Definimos
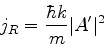 |
(152) |
como a densidade de corrente refletida, e
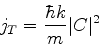 |
(153) |
como a densidade de corrente transmitida. Então, devemos ter
(para que não desapareçam partículas),
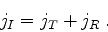 |
(154) |
Definido os coeficientes de reflexão e transmissão por
podemos então escrever a relação entre as correntes como
 |
(157) |
Note que a densidade de corrente dentro da barreira
é zero (calcule!). Logo, usando
 |
(158) |
vemos que, dentro da barreira,
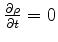 ,
ou seja,
,
ou seja, 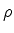 é constante. Logo, não há variação no
número de partículas, dentro da barreira.
A continuidade das funções de onda e suas derivadas em
é constante. Logo, não há variação no
número de partículas, dentro da barreira.
A continuidade das funções de onda e suas derivadas em
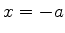 e
e  dá as seguintes condições:
dá as seguintes condições:
(i) Para 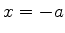 :
:
(ii) Para  :
:
Dividindo (161) por (162):
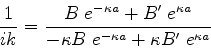 |
(163) |
de onde se tira
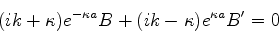 |
(164) |
Como a função de onda dentro da barreira é
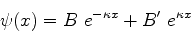 |
(165) |
temos, escrevendo 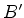 em termos de
em termos de 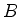 ,
,
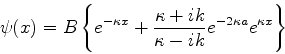 |
(166) |
onde se vê que o termo dominante é a exponencial decrescente
 .
.
Voltando à equação (161), obtém-se facilmente
que
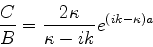 |
(167) |
e
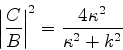 |
(168) |
Vamos introduzir as quantidades
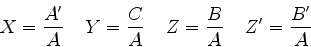 |
(169) |
As equações
(159),(160),(161),
(162) então ficam:
Como
 ,temos
,temos
 |
(174) |
Introduzindo os símbolos auxiliares
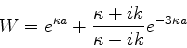 |
(175) |
e
 |
(176) |
podemos, após alguma álgebra, obter
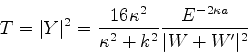 |
(177) |
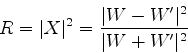 |
(178) |
e
 |
(179) |
de onde se vê que o comportamento assintótico
de 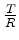 é dado por
é dado por
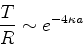 |
(180) |
que revela, ao mesmo tempo, a inevitabilidade do
tunelamento (a ausência de tunelamento seria
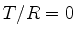 ) e se trata de um efeito pequeno, para
valores apreciáveis de
) e se trata de um efeito pequeno, para
valores apreciáveis de 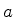 .
.
Posteriormente, quando estudarmos a aproximação
quase-clássica, seremos capazes de obter expressões
mais simples para o tunelamento.
Henrique Fleming 2003
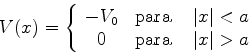
![\begin{pspicture}(0,0)(10,6)
\psline[linestyle=dashed]{->}(1,1)(1,6)
\psline[l...
...(2.3,4.2){$-a$}
\uput[0](6.8,4.2){$a$}
\uput[0](8.7,3.7){$x$}
\end{pspicture}](img289.png)
![\begin{displaymath}
\left[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+ V(x)\right]\phi(x)=E\phi(x)
\end{displaymath}](img296.png)

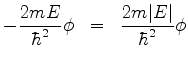
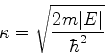
![]() , e a equação é
, e a equação é
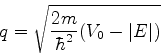
![\begin{pspicture}(0,0)(10,6)
\psline[linestyle=dashed]{->}(1,1)(1,6)
\psline[l...
...(2.3,4.2){$-a$}
\uput[0](6.8,4.2){$a$}
\uput[0](8.7,3.7){$x$}
\end{pspicture}](img289.png)
![]() ) exigimos que
) exigimos que
![]() e
e
![]() , onde
, onde ![]() é a solução na região I, e
é a solução na região I, e ![]() é a solução
na região II. Para conectar as regiões II e III, agimos da mesma
forma:
é a solução
na região II. Para conectar as regiões II e III, agimos da mesma
forma:
![]() ,
,

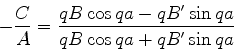
![]() temos as relações:
temos as relações:
![]() e
e
![]() , que são tais que
, que são tais que
![\begin{displaymath}
-\frac{\xi}{\eta}=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2-\xi^2\right]^{-\frac{1}{2}}
\end{displaymath}](img358.png)
![]() e
da função que está no segundo membro de (106). Onde as
curvas se cortem estarão os valores de
e
da função que está no segundo membro de (106). Onde as
curvas se cortem estarão os valores de ![]() que são as soluções
de (106).
que são as soluções
de (106).
![\begin{displaymath}
f(\xi)=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2-\xi^2\right]^{-...
...{1}{2}}
=-\xi\left(\mathcal{A}^2-\xi^2\right)^{-\frac{1}{2}}
\end{displaymath}](img363.png)
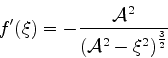

![\begin{displaymath}
\tan{\xi}=-\xi\left[\frac{2m}{\hbar^2}V_{0}a^2 -\xi^2\right]^{-\frac{1}{2}}
\end{displaymath}](img370.png)
{$1$}
\uput[0](7.3,2.0){$2$}
\end{pspicture}](img372.png)
![]() e a curva pontilhada é a função
e a curva pontilhada é a função
![]() . Os pontos
. Os pontos ![]() e
e ![]() correspondem às soluções
da equação.
correspondem às soluções
da equação.
![]() ).
).
![]() (soluções pares).
(soluções pares).
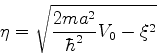
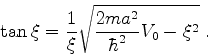
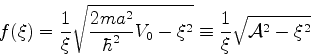
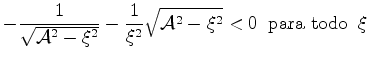
![]() , sempre
haverá ao menos uma solução.
, sempre
haverá ao menos uma solução.
![]() quando o
movimento da partícula é levado em conta.
quando o
movimento da partícula é levado em conta.
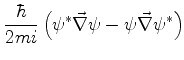
![]() essas réplicas. Se normalizarmos a função de onda de modo que
essas réplicas. Se normalizarmos a função de onda de modo que
{$V_{0}$}
\uput[0](6.1,7.5){$V(x)$}
\uput[0](11.8,1.8){$x$}
\end{pspicture}](img428.png)
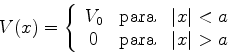
![]() temos as regiões I e III, onde a partícula não está sujeita
a nenhuma força. Nestes casos,
temos as regiões I e III, onde a partícula não está sujeita
a nenhuma força. Nestes casos,