Este é o problema mais simples envolvendo um sistema localizado. Uma partícula
move-se livremente ao longo do eixo 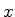 , exceto pelo fato de que, nas posições
, exceto pelo fato de que, nas posições 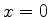 e
e 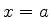 , existem paredes impenetráveis: exige-se, isto é, que a probabilidade de a
partícula estar fora do intervalo
, existem paredes impenetráveis: exige-se, isto é, que a probabilidade de a
partícula estar fora do intervalo
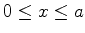 seja estritamente
seja estritamente 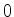 . Formalmente
isto se realiza exigindo que a função de onda da partícula seja nula nas paredes, que podem
ser consideradas infinitamente espessas. Portanto,
. Formalmente
isto se realiza exigindo que a função de onda da partícula seja nula nas paredes, que podem
ser consideradas infinitamente espessas. Portanto, 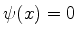 para
para 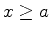 e para
e para
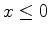 .
.
Procuremos os estados estacionários. Na região interna às paredes, temos
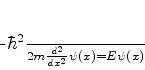 |
(52) |
onde 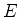 é um número positivo ou nulo. (O ``fundo do poço'' é o ponto
de energia zero, por definição). A Eq.(52) pode ser reescrita como
é um número positivo ou nulo. (O ``fundo do poço'' é o ponto
de energia zero, por definição). A Eq.(52) pode ser reescrita como
 |
(53) |
e, introduzindo
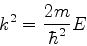 |
(54) |
temos
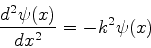 |
(55) |
Esta é uma equação diferencial bem conhecida. Sua solução geral é:
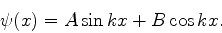 |
(56) |
Temos, adicionalmente, as condições de contorno
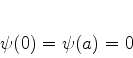 |
(57) |
Para satisfazer 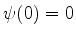 , basta tomar
, basta tomar 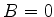 , pois o seno se anula automaticamente
em
, pois o seno se anula automaticamente
em 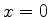 . Então, antes de usar a segunda condição de contorno, temos
. Então, antes de usar a segunda condição de contorno, temos
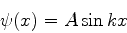 |
(58) |
A segunda condição de contorno exige que
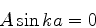 |
(59) |
e sabemos que o seno se anula em qualquer arco da forma  , com
, com 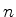 inteiro qualquer. Logo, devemos ter
inteiro qualquer. Logo, devemos ter
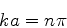 |
(60) |
ou seja, 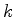 tem seus valores restritos aos da forma
tem seus valores restritos aos da forma
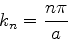 |
(61) |
onde acrescentamos um índice a 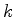 para maior clareza. Em
suma, as soluções da equação de Schrödinger
(52) que satisfazem as condições de contorno
(57) são
para maior clareza. Em
suma, as soluções da equação de Schrödinger
(52) que satisfazem as condições de contorno
(57) são
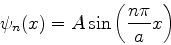 |
(62) |
com
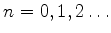 .9
.9
Note-se que é a condição de a função de onda se anular em 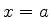 que restringe os valores
de
que restringe os valores
de 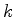 , e portanto os valores da energia , já que
, e portanto os valores da energia , já que
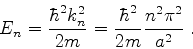 |
(63) |
Diferentemente do que acontece na física clássica, a energia não varia
continuamente: do valor 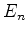 passa-se, a seguir, ao valor
passa-se, a seguir, ao valor 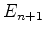 , e
, e
![\begin{displaymath}
E_{n+1}-E_{n}=\frac{\hbar^2}{2m}\frac{\pi^2}{a^2}\left[(n+1)^2-n^2\right]
=\frac{\hbar^2}{2m}\frac{\pi^2}{a^2}(2n+1)
\end{displaymath}](img275.png) |
(64) |
Temos, isto é, um espectro discreto para a energia . Espectros discretos
para a energia estão sempre ligados ao fato de o sistema ser localizado, isto é,
ter localização restrita a uma parte finita do espaço. Sistemas que podem estar em toda
a parte, como partículas livres, têm espectro contínuo.
É útil normalizar as funções de onda: os postulados interpretativos ficam mais simples,
quando isto é feito. Para tanto, vamos exigir que
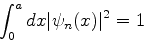 |
(65) |
ou
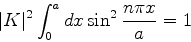 |
(66) |
Usando a relação
obtemos
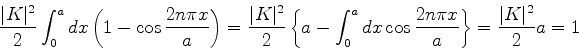 |
(67) |
Logo,
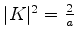 e podemos escolher
e podemos escolher
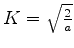 ,
já que a fase da função de onda é arbitrária. Assim,
,
já que a fase da função de onda é arbitrária. Assim,
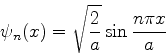 |
(68) |
leitor não terá dificuldades em mostrar o resultado mais geral:
 |
(69) |
que exibe a ortogonalidade das funções de onda correspondentes a energia s
diferentes.
A função de onda completa para esses estados estacionários
é então
 |
(70) |
com
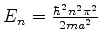 .
.
Estados não estacionários, na realidade estados quaisquer, podem ser obtidos
por combinações lineares desses 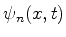 .
.
Henrique Fleming 2003
![]() que restringe os valores
de
que restringe os valores
de ![]() , e portanto os valores da energia , já que
, e portanto os valores da energia , já que
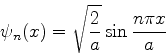

![]() .
.