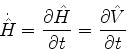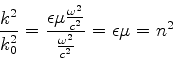- ... vida1
- ``The newer
concepts of physics can be mastered only by long familiarity with
their properties and uses'' (Dirac).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... arbitr\'aria2
-
Isto não está em contradição com as relações de
incerteza. Elas dizem que não é
possível determinar simultaneamente posição e momento .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... qu\^antico3
- Abuso de linguagem. Todos os sistemas
são quânticos. A expressão correta seria ``sistema incorretamente descrito pela física
clássica''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... coordenadas4
- Ou melhor, o elemento de
volume em termos dessas coordenadas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... \'e.5
-
Na realidade, há quantidades físicas também da forma
onde  é outra função de onda. Como essas quantidades também devem permanecer
inalteradas, é necessário acrescentar que a trasformação
é outra função de onda. Como essas quantidades também devem permanecer
inalteradas, é necessário acrescentar que a trasformação
deve ser tal que o mesmo 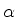 é usado para todas as funções de onda.
é usado para todas as funções de onda.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... completa.6
- Isto quer dizer que a função de onda de
cada uma das partes tem um ``futuro'' totalmente previsível, ou seja, que as duas partes do sistema
são independentes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...inuas.7
- Natura non facit saltus,
Isaac Newton.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....8
- Por exemplo, seja
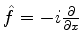 .
Então, dado
.
Então, dado 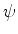 qualquer, temos
qualquer, temos
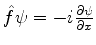 .
O operador
.
O operador 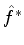 deve ser tal, então, que
deve ser tal, então, que
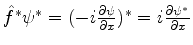 . Logo,
. Logo,
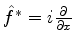 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....9
- Na realidade inteiros negativos são também admitidos,
mas, como
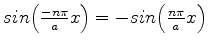 , as funções
de onda correspondentes a
, as funções
de onda correspondentes a 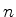 negativos são as mesmas que as de
negativos são as mesmas que as de 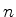 positivos, pois
positivos, pois
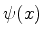 e
e 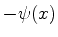 representam o mesmo estado.
representam o mesmo estado.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ivel.10
- O leitor
poderia se surpreender com a idéia de que uma partícula possa
ter energia negativa, mas esta é uma situação bastante comum.
Considere a ``partícula'' Terra, em seu movimento em redor da
``partícula'' Sol. A energia total da Terra é negativa! De
fato, precisamos realizar trabalho para levá-la ao ``infinito''
(livrá-la da ação do Sol) e deixá-la, lá, em repouso,
ou seja, com energia total zero. Logo, fornecemos energia à Terra
para levá-la a um estado de energia zero. Sua energia inicial
era, portanto, menor do que zero!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... alg\'ebricas11
- Uma equação
algébrica tem a forma de um polinômio igualado a zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Born12
- Max Born, grande físico teórico alemão, professor
em Göttingen, de quem Werner Heisenberg era assistente, quando
criou a mecânica quântica
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... carga13
- Por exemplo, ela diz que o seguinte fenômeno viola
a conservação da carga: uma carga desaparece aqui e aparece,
imediatamente depois, na nebulosa de Orion. Isto porque a equação
da continuidade exige que o desaparecimento de uma carga de dentro
de um volume seja acompanhado pela passagem da carga através da
superfície que delimita esse volume. Como isto é válido
para qualquer volume, a implicação é que, para uma carga
ir de um ponto ao outro, ela deve passar, continuamente, por
posições intermediárias. Daí o nome ``equação
da continuidade''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline19894#14
- Note que
(136) contém apenas os valores de
 na superfície S.
na superfície S.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
adiante,15
- O leitor há de perdoar esta pequena violação da
causalidade...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sistema.16
- Eqüivalentemente,
uma rotação
 sobre o sistema de eixos em
relação ao qual o sistema é referido.
sobre o sistema de eixos em
relação ao qual o sistema é referido.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Dirac17
- A
regra de Dirac diz: sejam
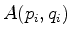 e
e 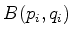 duas
quantidades físicas da mecânica clássica, e seja
duas
quantidades físicas da mecânica clássica, e seja 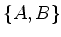 o
produto de Poisson (parênteses de Poisson) delas. Então, se
o
produto de Poisson (parênteses de Poisson) delas. Então, se
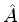 e
e  são os operadores hermitianos que
representam essas quantidades na mecânica quântica, temos a
igualdade simbólica:
são os operadores hermitianos que
representam essas quantidades na mecânica quântica, temos a
igualdade simbólica:
Ou seja, para obter o valor do comutador, calcula-se o produto de
Poisson das quantidades clássicas correspondentes,
multiplicando-se o resultado por 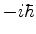 . Exemplo:
. Exemplo:
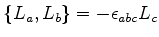 . Logo,
. Logo,
![$[\hat{L}_a,\hat{L}_b]=
i\hbar\epsilon_{abc} \hat{L}_c$](img818.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:18
-
Naturalmente eles não sabiam mecânica quântica, mas estudavam vibrações de corpos elásticos.Um dos
problemas dessa área, por exemplo, é a determinação das frequências que um tambor, de determinada forma,
pode emitir. Trata-se de um problema de autovalores : as freqüências emitidas são as autofreqüências.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... popular.19
- O leitor dedicado
gostará de investigar por que não aparece também um potencial
correspondente às forças de Coriolis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... assint\'otico.20
- Ver, por exemplo, Dicke,
Wittke,Introduction to Quantum Mechanics, página 161.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Bohr!21
- Exercício: no modêlo pré-quântico de Bohr, das
órbitas de momento angular
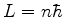 , determine o raio da menor
órbita estacionária. Você deverá encontrar
, determine o raio da menor
órbita estacionária. Você deverá encontrar 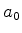 , o raio de Bohr.
, o raio de Bohr.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sabido,22
- No caso improvável de isto não ser
bem sabido por um aluno do CCM, aí vai:
ou seja,
etc.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....23
- Estritamente,
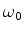 é a ``freqüência circular''. A verdadeira freqüência, que
é o inverso do período, é
é a ``freqüência circular''. A verdadeira freqüência, que
é o inverso do período, é
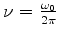 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ordem24
- O leitor
arguto estará perguntando: mas eu posso mudar a fase só do
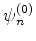 ? A mudança de fase permitida não é uma
mudança de fase simultânea para todos os estados?
Não, leitor arguto. Um mesmo estado é descrito pela classe de todos
os vetores de módulo 1 que diferem apenas por uma fase constant. No
entanto, por curiosidade, vamos mostrar que, neste caso, a mudança
de fase pode ser vista como uma mudança geral de fase. Examinemos a
Eq.(505) em maior detalhe. O resultado obtido, para
? A mudança de fase permitida não é uma
mudança de fase simultânea para todos os estados?
Não, leitor arguto. Um mesmo estado é descrito pela classe de todos
os vetores de módulo 1 que diferem apenas por uma fase constant. No
entanto, por curiosidade, vamos mostrar que, neste caso, a mudança
de fase pode ser vista como uma mudança geral de fase. Examinemos a
Eq.(505) em maior detalhe. O resultado obtido, para
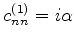 , é
, é
Mas, até primeira ordem, isto é o mesmo que
pois os termos
são de segunda ordem!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... perturbativo25
- Sim, leitor arguto. É redundante! Mas, didaticamente, é
útil, porque é simples, e é um caso em ue se pode
verificar o resultado.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... anular26
- Ou seja, as combinações
lineares escolhidas devem diagonalizar a matriz de elementos
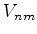 , na notação
da Eq.(529).
, na notação
da Eq.(529).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...energia27
- De fato, a fórmula
precisa, quando há dependência explícita no tempo no operador  , ser modificada,
dando
, ser modificada,
dando
Aplicando-se esta última equação ao hamiltoniano 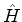 , tem-se
, tem-se
que é diferente de zero. Na mecânica quântica, lembre-se, a conservação da
energia é sumarizada pela relação
 , que, neste caso, não é verdadeira.
, que, neste caso, não é verdadeira.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Riemann-Lebesgue28
- O
leitor achará uma descrição breve em
http://mathworld.wolfram.com/Riemann-LebesgueLemma.html
e uma longa em qualquer livro que trate de integral de Lebesgue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Waals29
- Errado! Veremos mais abaixo que esta força existe, mas
que a atração de van der Waals ocorre também para moléculas rígidas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vetorial30
- Dito produto tensorial
dos espaços
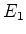 e
e 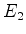 , e denotado, quando se quer
assustar os estudantes, por
, e denotado, quando se quer
assustar os estudantes, por
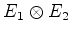 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mutandis31
- Um latinzinho faz sempre bem! Quer dizer,
mudando o que deve ser mudado.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... anti-paralelos32
- Linguagem de mesa de bar. Corretamente, isto se
diria assim: dois elétrons podem estar em estados
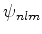 para os mesmos valores
de
para os mesmos valores
de 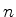 ,
, 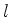 e
e 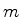 , desde que suas componentes
, desde que suas componentes 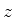 do spin tenham sinais opostos. Mas não
se fala assim num bar...
do spin tenham sinais opostos. Mas não
se fala assim num bar...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...quase-clássicos33
- O
método tratado nesta seção é também conhecido como Aproximação WKB (Wentzel, Krames, Brillouin).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
deles34
- Como é usual entre os físicos, estaremos,
indiferentemente, denotando o estado por
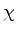 ou
ou 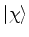 .
Em geral usa-se esta última forma quando se vai fazer uso de algum
dos truques da genial notação de Dirac
.
Em geral usa-se esta última forma quando se vai fazer uso de algum
dos truques da genial notação de Dirac
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... anti-unit\'ario35
-
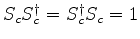 , mas
, mas
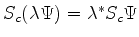
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... que36
- Por abuso de linguagem estamos representando pelo
mesmo símbolo,
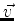 , tanto o vetor quanto a matriz coluna que
o representa numa base.
, tanto o vetor quanto a matriz coluna que
o representa numa base.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complexa37
- Sim, leitor! Trata-se de uma matriz
complexa, embora não pareça. Lembre-se de que
 é um número
complexo, pois pode ser escrito como
é um número
complexo, pois pode ser escrito como  !
!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nome38
- A famosa transformada de Laplace!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nota39
- Isto quer dizer que as energia s
consideradas são positivas, como é o caso para um oscilador harmônico
de energia potencial
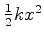
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...irculos40
- Bem, transforma círculos em elipses, mas, no
caso, a transformação é isotrópica, e transforma círculos em
círculos...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geom\'etrica.41
- Note que
onde 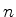 é o índice de refração do meio.
é o índice de refração do meio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline24496#42
-
Pois
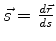 , temos que
, temos que
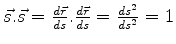 onde usamos que
onde usamos que
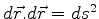
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... determinar43
- Em outras palavras, existe um
vetor
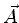 tal que a Eq.(1054) é satisfeita.
tal que a Eq.(1054) é satisfeita.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
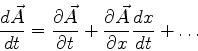
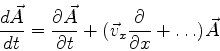
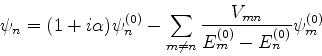
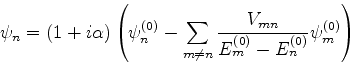
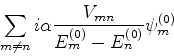
![\begin{displaymath}
\dot{\hat{O}}=\frac{\partial \hat{O}}{\partial t}+\frac{i}{\hbar}[\hat{H},\hat{O}]
\end{displaymath}](img1780.png)